Flip|Definition & Meaning

Theoretical Description 

The idea of any object being flipped comes from the deep roots of reflection, which we can see in any shiny surface; it may be of water or a mirror. When light falls on such surfaces, the particles are affected by the energy they receive in the form of light energy. They give off this energy in the form of the emission of photons. This is how we see ourselves in the mirror.

Flipped image can also be called the reflection of an image. We can flip an image only if it has any kind of symmetry or line symmetry. This line across which any object is inverted is called the line of reflection or axis of reflection. 

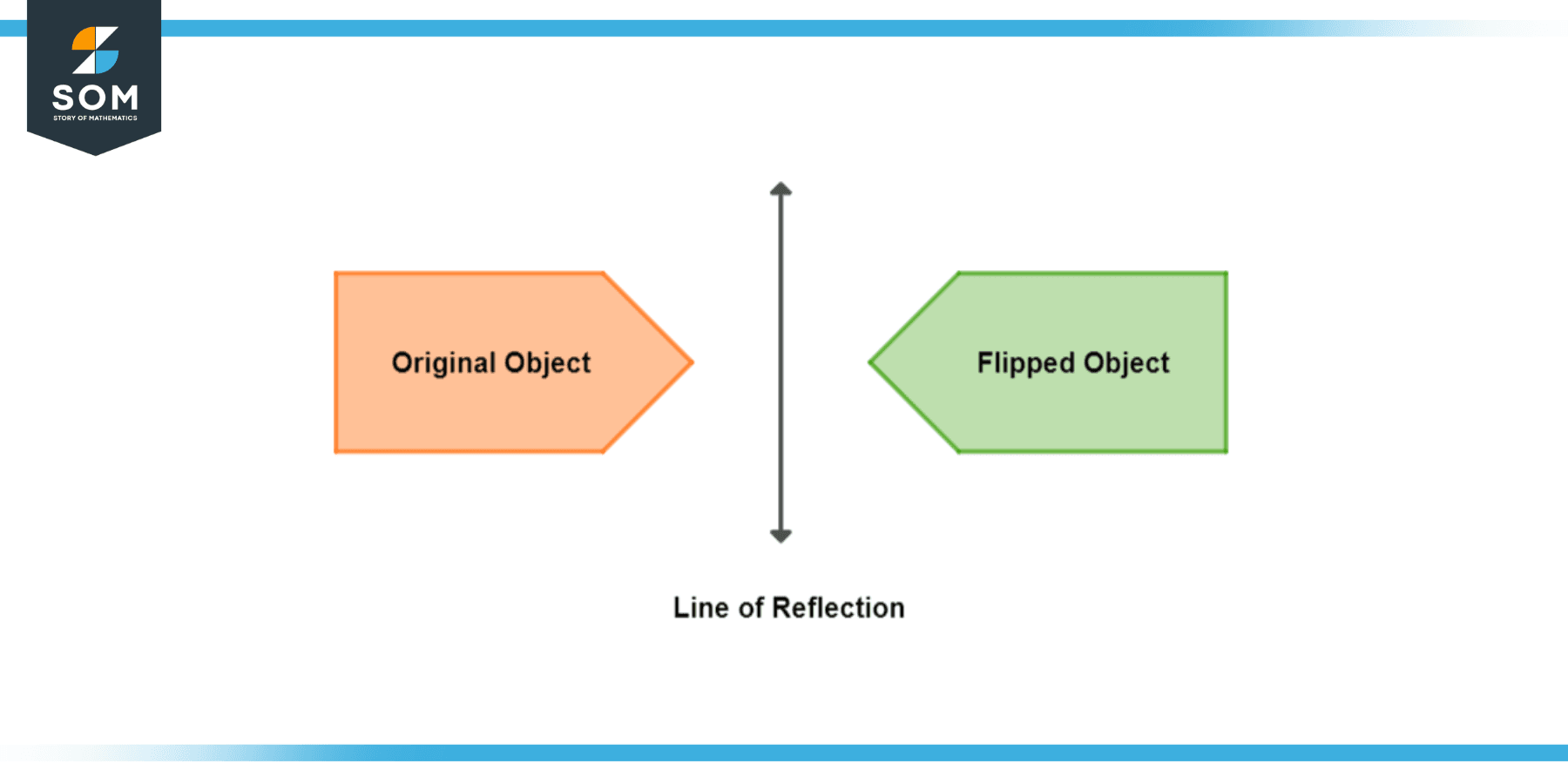
Figure 1 – The flipped image of an object

The importance of the line of reflection is that it lies between both images; origins and flipped image. So to find the distance between these two images, we can use the line of reflection. The distance between the original points of an image and the line of reflection is the same as that of the flipped image.

To understand the concept is to take a tracing paper. Now draw any object on it and flip the paper. After flipping it we will compare the image drawn on the tracing paper with the original image. The object might be on the opposite side but the image has been flipped

Types of Flips

Flipping is known as the reflection of any object or image in a plane. The image or an object can be flipped into different forms. These two are the types of flips that can be done on any object:

Vertical Flip

When an image is flipped in such a way that only the vertical part of the image is inversed then it is known as the vertical flip. Let us take a look at the following image:

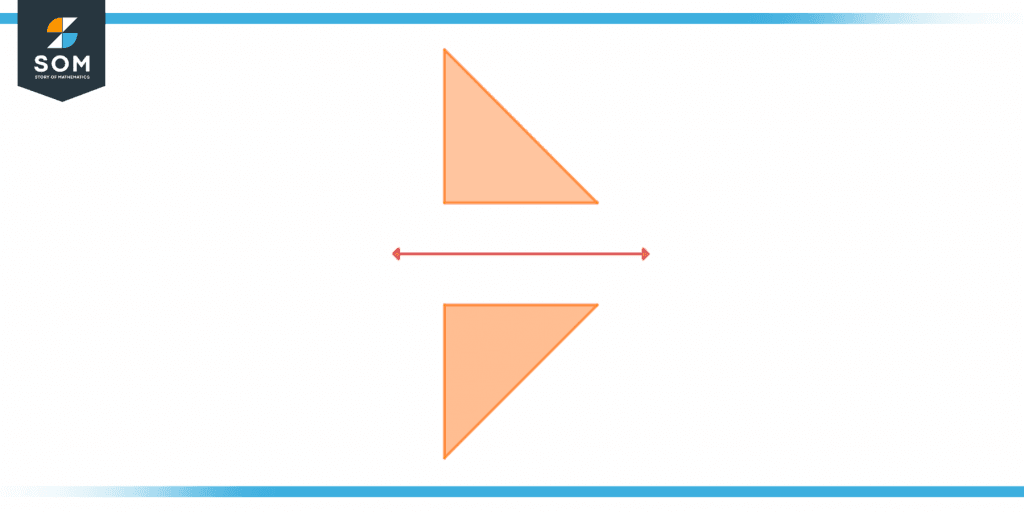
Figure 2 – Vertical flip of a triangle

In this image, the triangle has been flipped such that the object’s x-axis has changed but the y-axis remains the same.

If we have a certain set of coordinates and we draw a graph, and the x-axis acts as the line of reflection, then it is also known as a vertical flip. The following image shows the plotted image that has been flipped such that (x, y) becomes (x, -y). Hence x remains the same whereas the y is flipped to be negative.

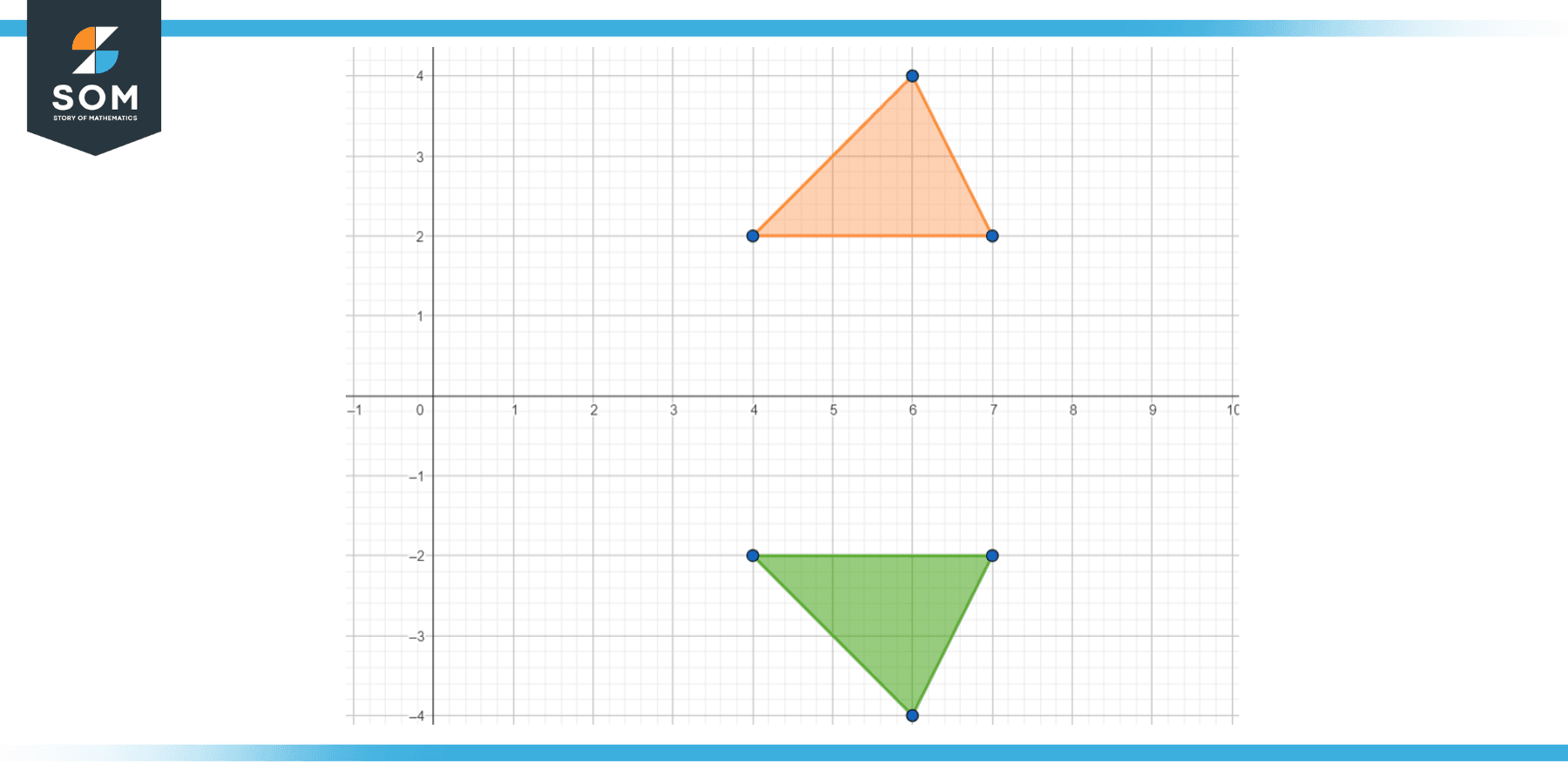
Figure 3 – Flipped graph of x and -y

Horizontal Flip

A horizontal flip is an image that is inversed such that the horizontal part changes but the vertical part remains the same. Let us take an example to understand the concepts:

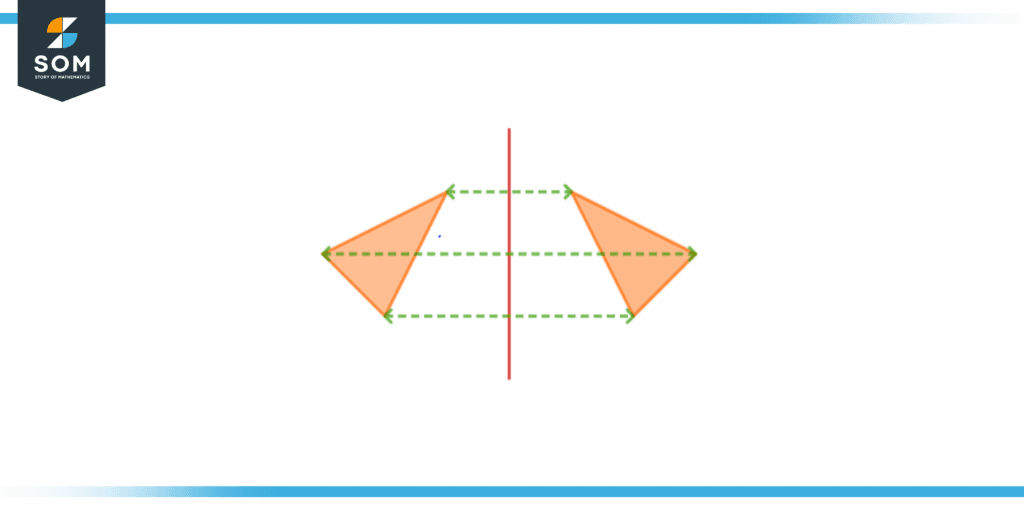
Figure 4 – Horizontally flipped image of a triangle

In this image, the triangle has been flipped in such a way that the y-axis of the object has changed, but the x-axis remains the same. 

When we are plotting an object by using some coordinates, and the y-axis acts as the line of reflection, then we call it the horizontal flip. The following image shows the plotted image that has been flipped such that (x, y) becomes (-x, y). Hence y remains the same, whereas the x is flipped to be negative.

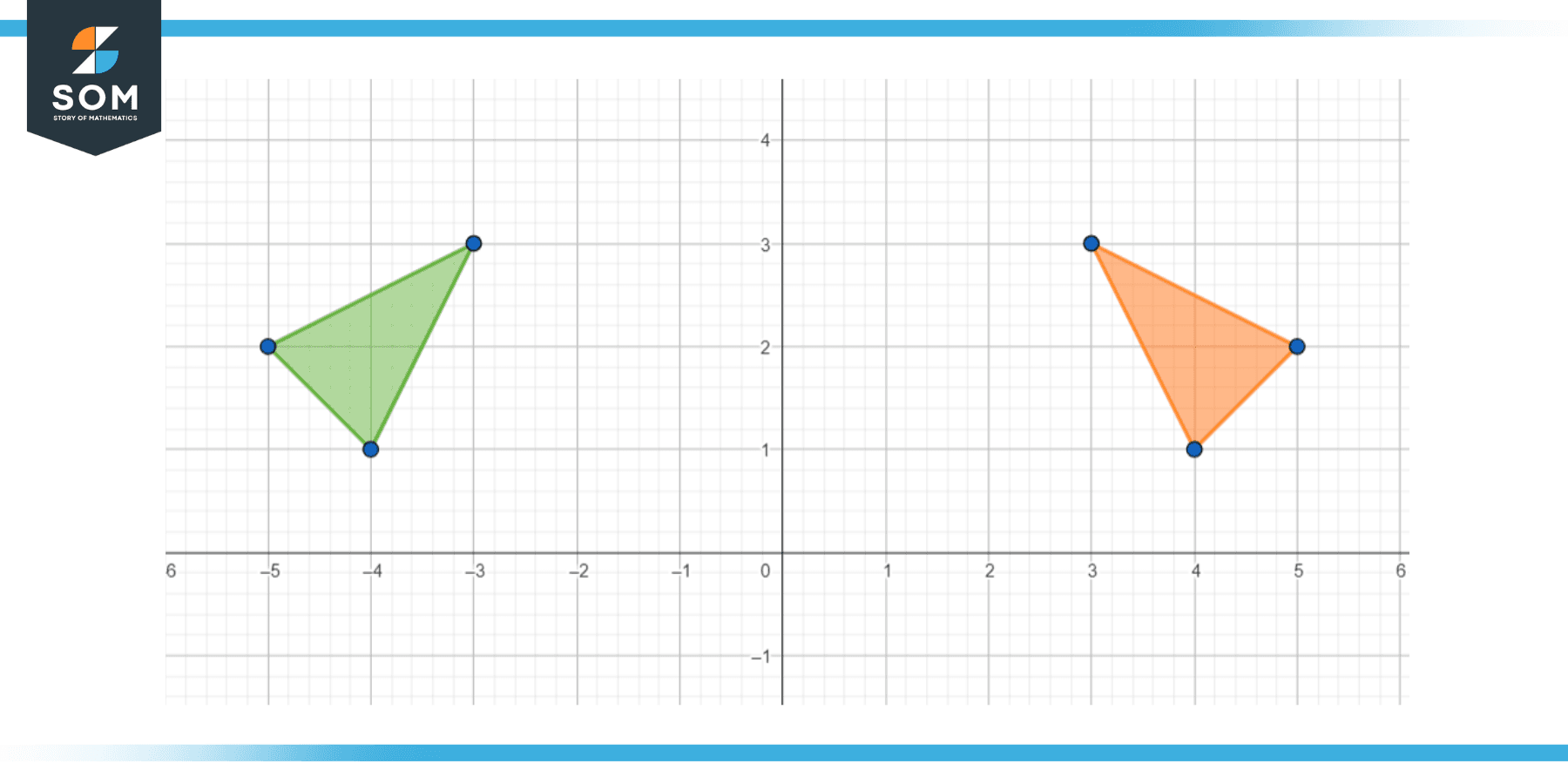
Figure 5 – Flipped graph of -x and y

Pictorial Representation

Flipping an image is just writing something on a piece of paper and reading it out using the mirror’s reflection. All the text becomes inverted and hard to read. Just like that, we will see how certain objects are flipped.

The following image shows the original object, which has been flipped horizontally and vertically concerning its axis.

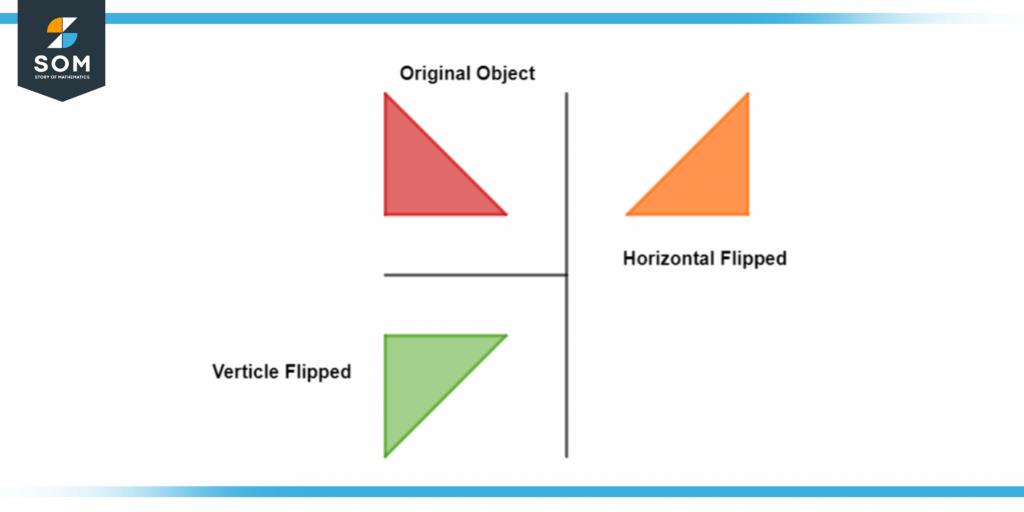
Figure 6 – Vertical and Horizontal flipped object

Here the line of reflection is equidistant from each object, and hence if we want to find the distance between these objects, we will use this line as the center point.

Solved Examples

Example 1

Juno was assigned a task for his homework. He has to correctly tell what will be the flipped image of the following object:

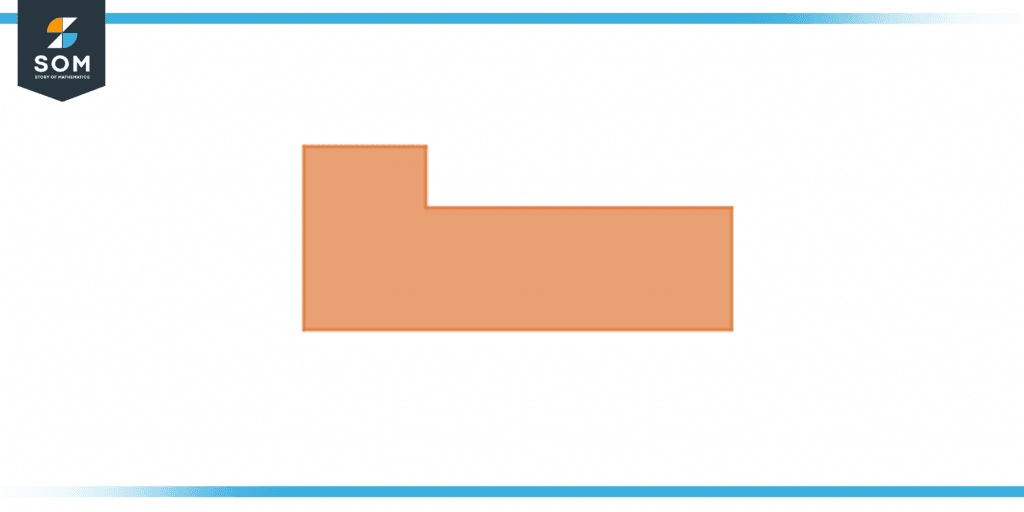
Figure 7 – An irregular object on the XY plane

Explain your answer.

Solution

The object in the image is an irregular object which is why when it is flipped, the change will be quite prominent compared to any regular object. The following image will form when this object is flipped.

Figure 8 – Flipped irregular object on XY plane

Example 2

Harper has the coordinates of an object in an XY plane:

(2, 3), (3.5, 4), (5, 3), (4.5, 1.3), (2.8, 1.2)

She wants to Flip these coordinates to see what coordinates she will get as a result. Help her find the flipped object’s coordinates.

Solution

When we are converting any object into a flipped image, then we are going to change either the x-axis or the y -axis. So if we want to flip the object concerning the y-axis then the coordinates will be:

 (2, -3), (3.5,-4), (5, -3), (4.5, -1.3), (2.8, -1.2)

Here the x part of the coordinates will remain the same, whereas the y part will be negative. This is also known as the vertical flip. And if we flip the object concerning the x-axis then the coordinates will be:

(-2, 3), (-3.5, 4), (-5, 3), (-4.5, 1.3), (-2.8, 1.2)

Now the ‘y’ part of the coordinates will remain the same, whereas the x part will be negative. This is also known as the horizontal flip.

Example 3

Using your understanding, list real-life examples of flipping objects or images.

Solution

The Reflexive property of Flipping images is quite useful in real-life. Some of its examples are given below:

1. We use Flipped Text on ambulances. The purpose behind using flipped text is to help the drivers read the labels on the ambulance from their side mirror and let an ambulance pass through. This helps the drivers to avoid any traffic hazards as they can easily read signs without being distracted.
2. It helps artists to set new themes and tones in their images and photos. Similarly, it is used in Rear Window Captioning System for people who have a difficult time understanding any video or movie. This text lets them easily understand the content.

Images/mathematical drawings are created with GeoGebra.

Flat Definition < Glossary Index > Foil Method Definition