JUMP TO TOPIC

Foil Method|Definition & Meaning

Definition

The FOIL Method is used to calculate the product of binomials. The acronym ‘FOIL’ stands for First, Outside, Inside, and Last which refers to the arrangement of multiplying terms. We multiply the first element, then the outside element, then the inside element, then the last element, and then combine like terms for our answer.

The general form of the above explanation can be depicted below:

Figure 1 – Foil General Form

FOIL is an abbreviation for the classic method of multiplying the two binomials, therefore named ‘FOIL.’ The word FOIL represents the four terms of the product, as explained next.

‘F’ for “first” represents that the first terms of each binomial are multiplied together. ‘O’ for “outer” means that the first element of the left binomial and the last term of the right side binomial are multiplied. ‘I’ for “inner” represents that the last element of the left binomial and the first element of the right side binomial are multiplied.

Finally, ‘L’ for “last” represents that the last terms of each binomial are multiplied.

FOIL Formula

The FOIL Method utilizes the distributive property to expand the product of two polynomials. The acronym FOIL (First-Outside-Inside-Last) is derived from the process used to expand the two binomials.

The concept of the FOIL method has been described in Figure 2 for the following example:

(a+b)(c+d) = ac + ad + bc + bd

i.e. the product of binomials (a+b)(c+d) is the sum obtained by:

Multiplying the First terms.
Multiplying the Outer terms.
Multiplying the Inner terms.
Multiplying the Last terms.

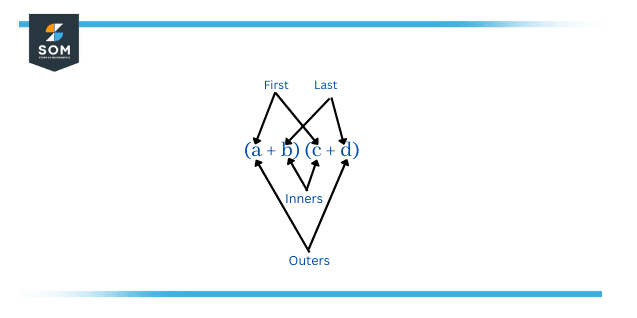
Figure 2 – Foil Depiction

Background Concepts

Binomials

A binomial is an expression having two numbers or variables, sometimes called two terms, that are separated by a sign of addition or subtraction.

We know that a variable is a letter that represents something. Let’s take a look at this example of a binomial, i.e., x + 10, as shown in Figure 3.

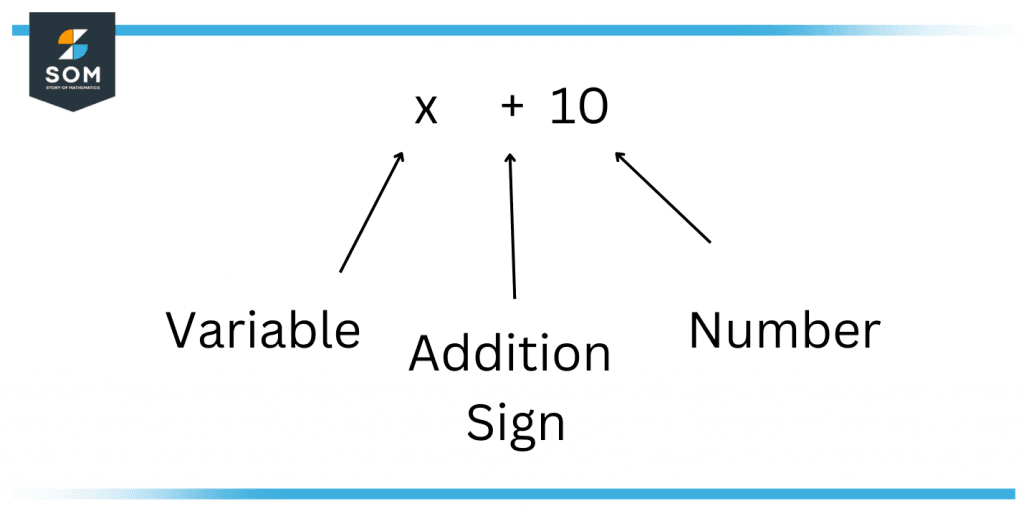
Figure 3: Concept of Binomials

Note that this is a binomial because this polynomial contains two terms that are separated by a plus sign where x is a variable and 10 is a constant. Another example of a binomial is ‘x + 1,’ which also contains two terms that are separated by an addition sign. Now, if we need to multiply these two binomials, one easy way to multiply them is to use the FOIL method!

Multiplying three binomials like the above pairs is an extension of the case for standard FOIL. One needs to pair off two binomials at a time to perform multiplication.

Distributivity

In binary operations involved in mathematics, the distributive property generalizes the distributive law, which is represented by the equality

a × (b + c) = (a × b) + (a × c)

This equality is always true in elementary algebra. The variable or number that is outside the brackets is been multiplied by every element present inside the brackets, and later the answer of individual products are summed up.

Proof of FOIL Method

To start with, let’s consider that the following standalone equation is given:
(a+b)(c+d) = ac+bd+bc+bd

and we want to multiply the binomials appearing on the left-hand side. The target is to prove that the left-hand expression of the relation can be rearranged to become equal to the right side. One of the first steps of this proof is to note that the above goal can be rephrased. It is similar to showing that the right-hand expression is similar to the left-side expression.
ac+bd+bc+bd = (a+b)(c+d)
The above relation is known as flipped expansion of the binomial equation.

Given the left-hand side of the equation, we can utilize multiple ways to rearrange the variables.

Algebraic Context of FOIL Method

Before we discuss the details of algebraic context, let’s take a small detour to further investigate the hypotheses and properties of this verification. For now, we’ll consider our binomial variables to be the real numbers.

It might be obvious that we plan on utilizing certain properties. This query points out another hypothesis because our variables or numbers in binomial permits us to apply additive or multiplicative axioms. Regarding algebraic context, the concept of ‘field’ needs to be clarified. A ‘field’ represents a set that satisfies the following identities:

Associative property of addition: a + (b + c) = (a + b) + c
Associative property of multiplication: a ⋅ (b ⋅ c) = (a ⋅ b) ⋅ c
Commutative property of addition: a + b = b + a
Commutative property of multiplication: a ⋅ b = b ⋅ a
Additive property: there exists a ‘0’ so that for any ‘a’ in the field, a + 0 = a
Multiplication property: there exist a ‘1’ as an element so that for any ‘a’ in the field, a ⋅ 1 = a
Additive property of inverses: for every ‘a’, there exists a ‘−a’, which is called the additive inverse so that a + (−a) = 0.
Inverse for Multiplication: for every a ≠ 0, there exists a ‘1/a’, so that a ⋅ 1/a = 1.
Distributive property of multiplication and addition: a ⋅ (b + c) = (a ⋅ b) + (a ⋅ c).

All these properties seem very evident to us — we have understood these axioms from a young age. However, there lies the assumption that we are always working in a field. This is not always true.

Now, how does this concept of field apply to our problem? Well, we presumed that the numbers or variables considered binomial are real numbers. Real numbers are verified to be a field, therefore permitting us to take benefit of the above properties in our algebraic manipulations.

As mentioned in the above section, in multiplication, distributivity, and for addition, commutativity plays an important part in the process of proof. In fact, as far as the binomial elements belong to a set that satisfies these two pre-requisite properties, the FOIL relation will hold.

Solved Example

Example

Evaluate:(4x + 5)(3x + 2)

Solution

As FOIL Formula says:

(4x + 5)(3x + 2) = (4x * 3x + 4x * 2) + (5 * 3x + 5 * 2)

(4x + 5)(3x + 2) = (12x² + 8x + 15x + 10)

(4x + 5)(3x + 2) = (12x² + 23x+ 10)

All images/mathematical drawings were created with GeoGebra.