JUMP TO TOPIC
Foot|Definition & Meaning
Definition
Foot is a measuring unit of length or distance. The abbreviation of foot is ft. The foot is a single unit of measurement whereas feet is the plural of foot. The standard symbol for foot is “ ‘ “.
The foot is a primary unit of length in the US system of measurement. One foot is equal to 12 inches. One foot has been precisely defined as 0.3048 meters. One foot equals 12 inches in both customary and imperial units, and one yard equals three feet.
Foot Illustration
When discussing the historical significance of the foot, the local system employs this unit. This system is used by the Greeks, Romans, French, Chinese, and French. Furthermore, foot length differs from country to country and also from city to city.

Figure 1 – Foot and Feet
In our daily lives, we measure objects. To measure the size of an object, we use various units such as meters, centimeters, inches, feet, and so on. A proper unit of measurement is based on the shape and size of the object. For example, the measuring unit of the height of a pen is cm.
There are two measurement systems: the imperial system and the metric system. The foot, as well as feet, are SI measurement units. They allow us to determine the length of an object or person. They can also assist us in determining the distance between two points.
Foot and Feet
A ‘foot’ refers to a single measurement unit, and ‘feet’ is the plural form. In this context, the deviation between foot and feet in Math is determined by the value of the length or distance being measured.
Understanding the difference between foot and feet in Math is important for knowing how much further something is or its size. We can make objective comparability by implementing the unit to various objects or distances.
Similarly, the foot is the proper measurement unit for measuring a table’s height.
The metric system includes meters, centimeters, and other units, while the system of imperial includes feet, inches, yards, and other units.
Relation Between Foot and Inch
1 foot =12 inches
1 inch = 1/12 inches
For example, if a rod is 24 inches high, it means the rod is 2 feet.
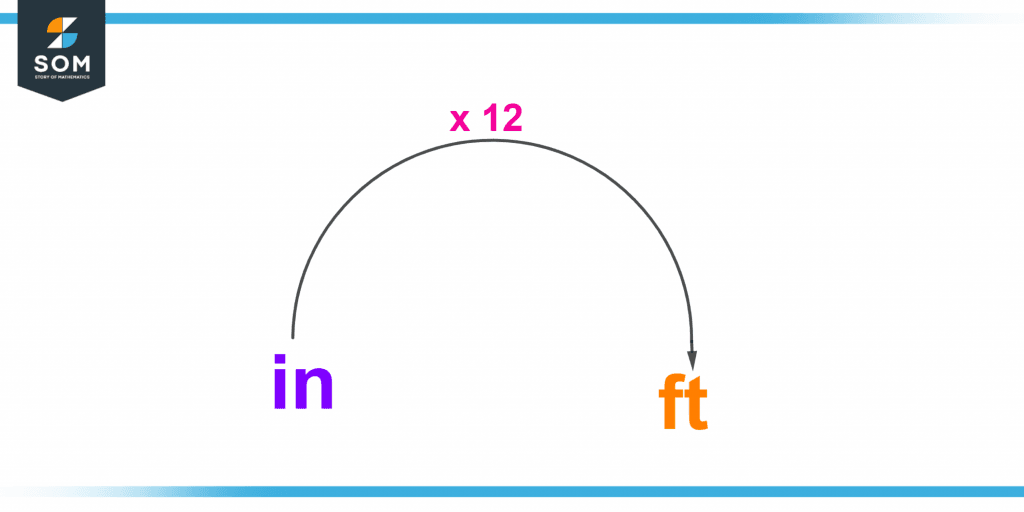
Figure 2 – One foot is equal to twelve inches
While trying to convert measurement results from inches to feet, we occasionally obtain the quotient in decimals. Rather than converting the value to decimals, expressing it in both inches and feet is more convenient.
50 feet equals 4 feet and 2 inches because dividing 50 by 12 yields 4 as the quotient and 2 as the remainder. The remainder value will be written in inches and quotient as feet in the division.
Relation Between Foot and Yard
The length is measured in yards and feet. Both US customary and imperial measurement systems employ both units. Three feet equal one yard.
1 yard = 3 feet
1 foot= 1/3 yard
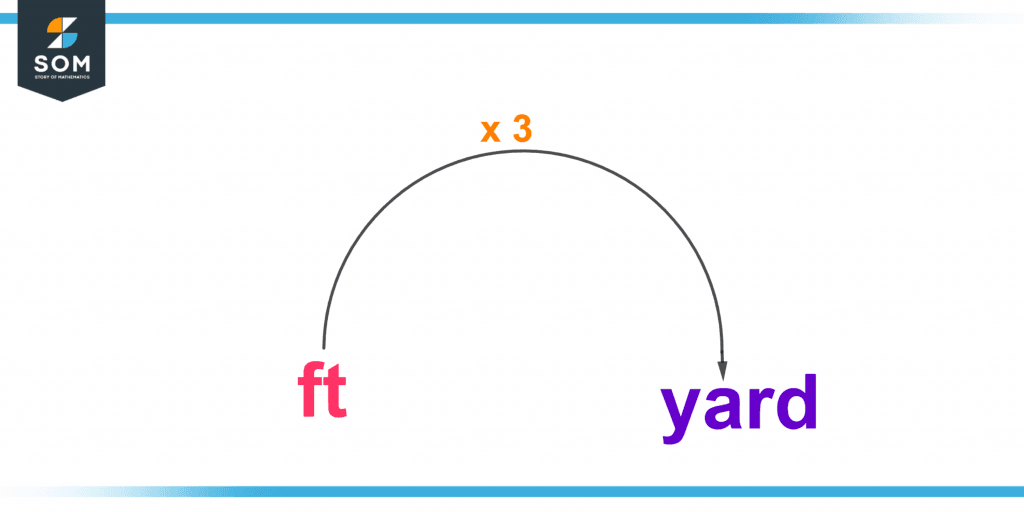
Figure 3 – One yard is equal to 3 feet
For example, a park is 12 yards long, and we must fence it in feet. To calculate the park’s length in feet, divide 12 by three, which equals four feet, so to cater to the whole park, 4 feet fence would be needed.
Relation Between Foot and Meter
A meter is a unit of displacement or length in the International System of Units (SI). Furthermore, one meter is nearly 39.37 inches, and a foot is approximately 0.3048 meters.
1 meter ≈ 3.28 feet
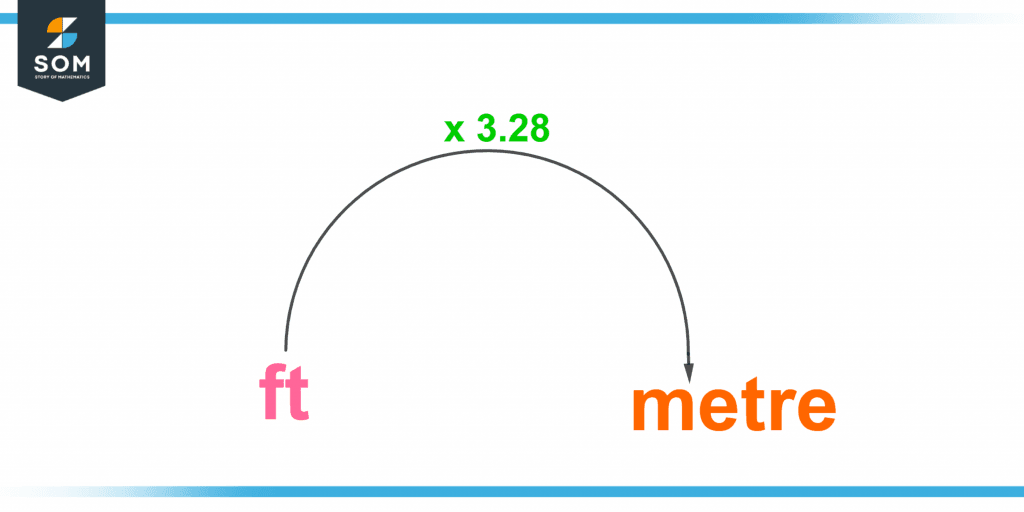
Figure 4 – Feet to meter
For example, if a pipe is 4m high, then it is approximately 4 x 3.28 = 13.12 feet high.
Relation Between Foot and Centimeter
The feet-to-centimeter calculator converts measurement units from feet to centimeters. Feet are denoted by “ft,” and centimeters by “cm.” The centimeter is a core component of the metric system and is utilized in the International System of Units. One foot is estimated to be 30.48 centimeters long.
1 foot ≈ 30.48 cm
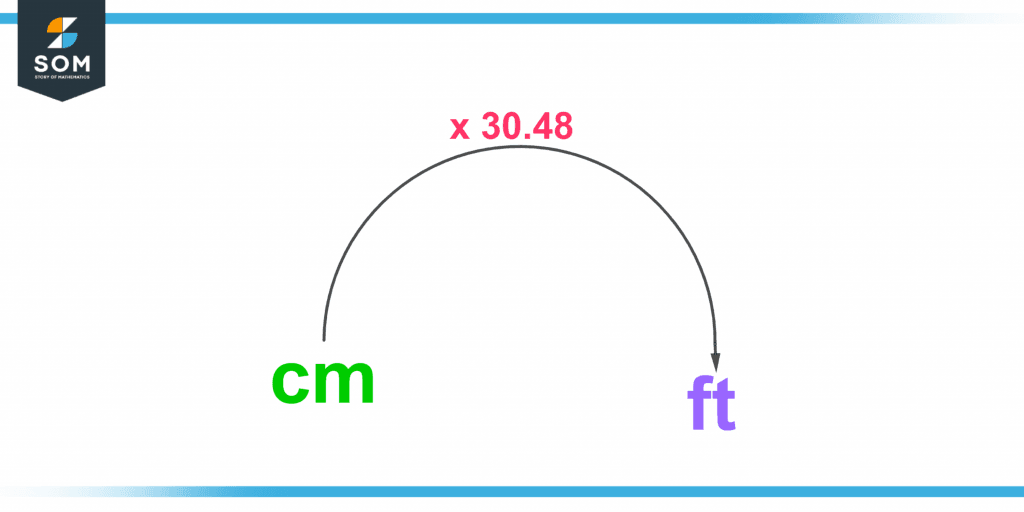
Figure 5- Centimeter to foot
For example, if the height of a man is 6 feet, it is approximately 6 x 30.48 = 182.88 cm.
Examples of Dimensions in Feet
Example 1
A square has a length of 24 inches. What would be the length of the square in feet?
Solution
1 foot = 12 inches
2 x feet = 2x 12 inches
2 feet = 24 inches
So the length of the square will be 2 feet.
Example 2
What is the area of a triangle (square feet) if its base is 60 inches and its height is 48 inches?
Solution
Area of triangle = 1/2 (length x base)
=1/2 (60 x 48)
1/2(2880)
=1440 inches²
We need to convert this area into feet square for that
12 inches= 1 foot
1440 ⁄12 inches = 120 feet
So the area of the triangle is equal to 120 feet square.
Example 3
The distance between the two points, X and Y, is 30 feet, and the distance between Y and Z is 18 meters. So, in feet, what is the separation between X and Z?
Solution
The distance between points X and Y = 30 feet, and the distance between points Y and Z = 18 m. We need to find the distance between points Z and A.
From the above conversions, we know that:
1 m = 3.28 feet
So:
18 m = 3.28 x 1818 m = 59.04 feet (approx)
So the distance between Z and X will be the sum of the distances between XY and YZ:
Distance between Z and X = Distance between XY + Distance between YZ
Distance between Z and X = 30 feet + 59.04 feet
Distance between Z and X = 89.04 feet
All the figures above are created on Geogebra.
