JUMP TO TOPIC
Function|Definition & Meaning
Definition
A function is basically a rule that determines the relationship between a dependent and an independent variable. That is, it relates the input with the output, or “maps” the input set to a set of output values.
The Function is symbolized as y= f(x), where f(x) is called the function of x. Here, y and x are related to each other for each value of x we have a unique value of y. There must be one value of output for each value of the input.
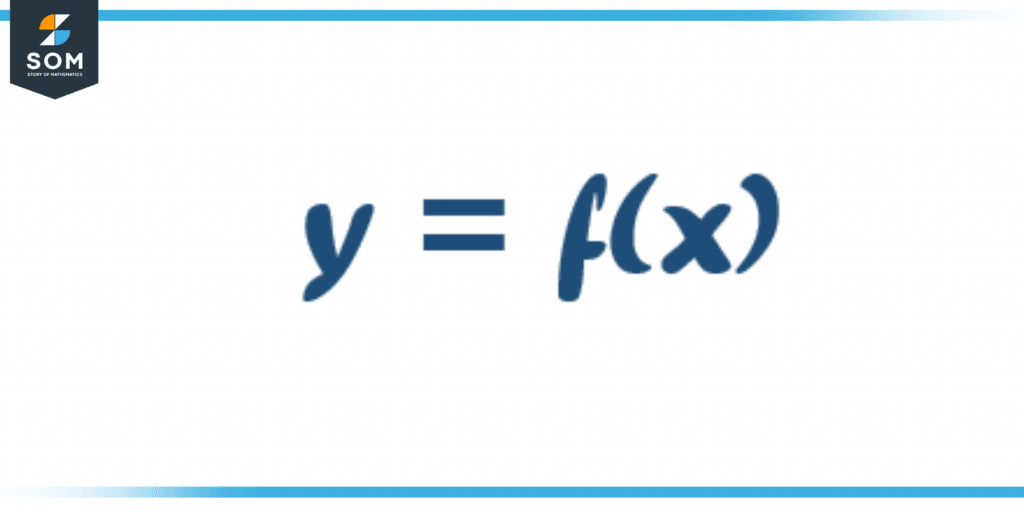
Figure 1: y equals to function of x.
Here f(x) is a function of x which is giving a new value at every value of x.
What Is Function?
If every element of set X has exactly one image in set Y, the relationship is known as a function. A function is a relation or process that connects every element ‘x‘ of a non-empty set X to at least one other non-empty set Y. In mathematics, a function is a relation from one set X which is the domain of that function to another set Y which is the co-domain of that function.
If every element of set X has exactly one image in set Y, the relationship is known as a function. A function is a relation from a set X which is a non-empty set Y with the domain X and no two different pairs in function f having the identical first element.
Function in Maths
Functions are the foundation of calculus in mathematics. There are various types of relationships. In mathematics, a function is represented as a rule that generates a distinct output for each input x. In mathematics, modeling or mapping is used to symbolize a function. Such functions are usually represented by letters like f, g, and b.
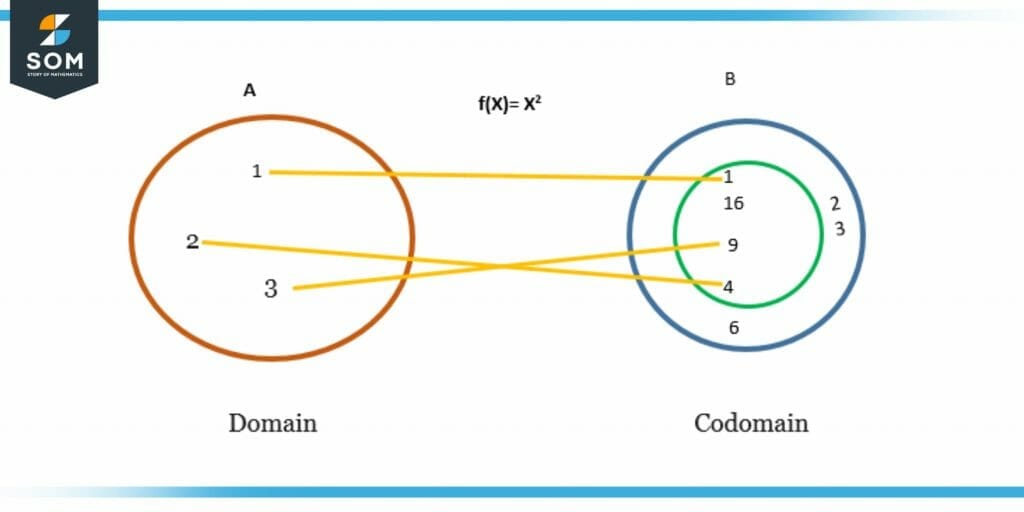
Figure 2: Function of a square in maths
The domain is a set of all possible values for which the function can be defined. The range or codomain includes all of the values returned by the function in question. A co-domain is a set of values that can be outputs of a function. Let us delve into the world of mathematical functions.
Types of Function
There are different types of functions and nonfunctions like composing functions, one-to-one functions, many functions, and complex functions, etc some of the functions are defined below.
One-to-One Function
A function is said to be one-to-one when there is just one x value, such as y = f for each point y in its range (x), f(x) = x2 isn’t one-to-one because there are two x values such as f(x) = 4. A function on a graph is one to one function if any horizontal line trims the graph only once.
Many-to-One Function
A function is said to be many to one if many values of the first set matches or meet with one value of the other set. A function is giving one value at many inputs. So here the inputs are many but the output will be just one that’s why this type of function is called many to one function.
One-to-Many Function
Like the above two functions, this will also have a domain and range based on the input values and output values here, in this case, one input value or element will give many output values means one input will give many outputs as a result. But this is not a function because this will not follow the vertical line test. After all, when a vertical line makes to pass through the function line it will not cut once but it will cut many times so it is not a function.
Many to Many Function
The last type is many to many it means many input values will result in many output values so this type is many to many. Many to Many types is also not a function because it will also not follow the vertical line test.
Function of Graphs
Among the many kinds of functions that exist, some examples include identity functions, constant functions, quadratic functions, cubic functions, cube root functions, rational functions, modulus functions, and so on. When graphing functions, the independent variable is plotted along the x-axis, and the dependent variables are plotted along the y-axis. The points are then plotted in the cartesian plane using their coordinates.
There is not a single point on the graph that does not fulfill the EQs y = f. (x) requirements.
Example 1
Show f(x) as one to one function and many as a nonfunction.
Solution
The one-to-one function are those in which each element of inputs belongs to one or more than one element of the output, But two inputs will never belong to the same element in the output.
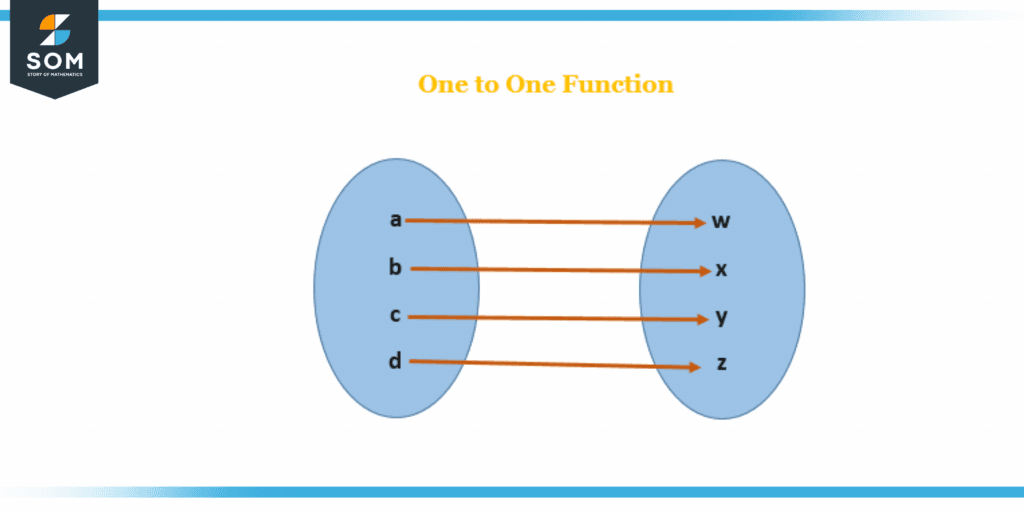
Figure 3: One-to-One function
Here in the figure above the one-to-one function is represented by each element in the first set belonging to each element of the other set. The first set which is input is the Domain of the function and the second set is the Range of the function.
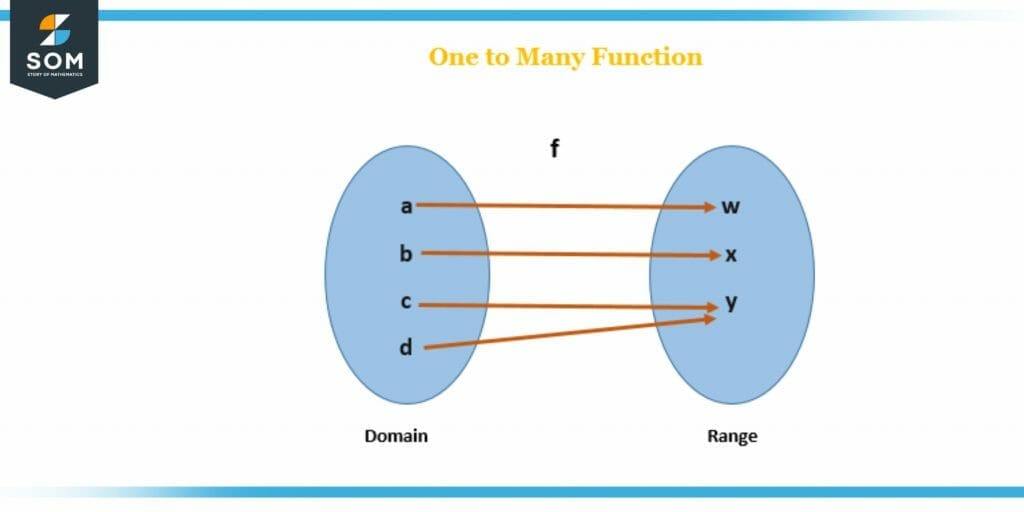
Figure 4: One-to-Many function
The above figure is also an example of the One to Many types. The figure itself is self-explanatory the Domain is the input, and the Range is the output. Every element of the input is combined with outputs, but here, in this case, each input has two output values as well. So this is an example of One too Many. But this is not a function because it will not follow the vertical line test.
Example 2
Graph the function of y = 1/x.
Solution
When there are no breaks in the graph of a function, we say that the function is continuous. The equation y = 1/x is an illustration of a graph that is discontinuous.
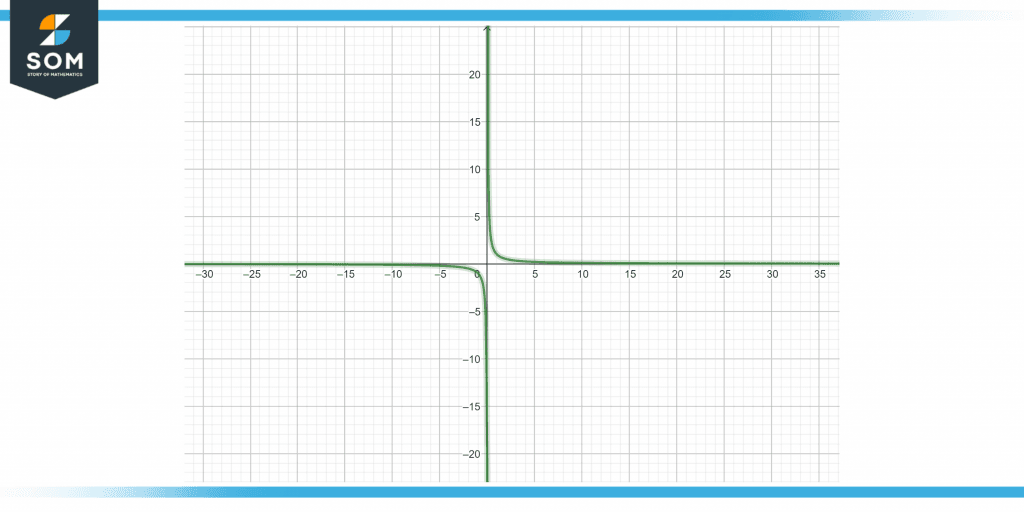
Figure 5 – Graph of function y= 1/x
A graph is said to be periodic in the context of a function if it keeps repeating itself at periodic intervals, with each of these intervals being referred to as the period.
When x is substituted with -x, a function is considered even if its behavior does not change. A function with this kind of symmetry will have a graph that is symmetrical along the y-axis. Even functions that are expressed as polynomials have degrees that are even (for example, y = x²).
If the sign of a function changes when x is changed by -x, then the function is considered to be odd.
All the figures above are created on GeoGebra.
