JUMP TO TOPIC
Geometry|Definition & Meaning
Definition
Geometry is mathematics’ branch of studying spatial relationships between objects of varying shapes and sizes. Geometry studies space and its figures, including their relationships, transformations, and angles.
Points, lines, angles, and flat surfaces are the primary building blocks of geometry. All other shapes in geometry can be derived from these principles.
What Is Geometry?
The term “geometry” comes from two Ancient Greek words: “Metron,” which means “Measuring,” and “Geo,” which means “Earth.” There are two-dimensional shapes, and there are also three-dimensional shapes in the geometry of Euclidean space.
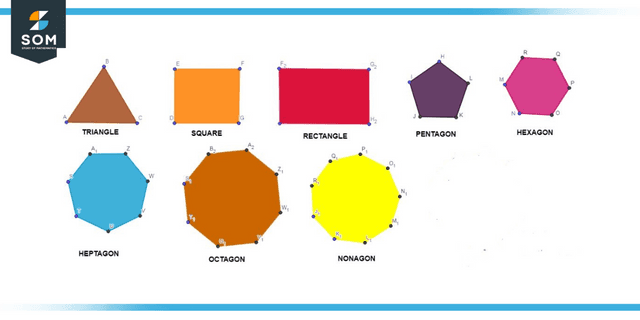
Figure 1: Geometry Shapes
In the field of plane geometry, the two-dimensional shapes known as flat shapes include circles, squares, rectangles, and triangles. In solid geometry, three-dimensional shapes such as a cube, cuboids, cones, and other similar shapes are also referred to as solids. The explanation of basic geometry may be found in coordinate geometry, which centers on points, lines, and planes.
In geometry, there are many various kinds of shapes, which helps us better grasp the shapes we encounter in everyday life. We can compute shapes’ area, perimeter, and volume using geometric ideas.
Subdivisions of Geometry
The subfields of geometry are:
- Algebraic geometry
- Discrete geometry
- The subject of differential geometry
- Euclidean geometry
- Convex geometry
- Topology
Geometry Based on Algebra
The zeros of multivariate polynomials are the subject of study in this subfield of geometry. It incorporates linear and polynomial algebraic equations, both of which are used in the zero set solution process. Applications of this kind include cryptography and string theory, amongst others.
Geometry With Discrete Spaces
It focuses on the relationships between basic geometric shapes, such as points, lines, triangles, and circles, among other things.
Differential Geometry
To solve problems, it applies problem-solving strategies based on algebra and calculus. Among the many issues at hand is general relativity in physics.
Euclidean Geometry
The study of solid figures and planes is based on theorems and axioms, including points, lines, planes, angles, congruence, and similarity. It finds use in various fields, such as computer science, solving problems in modern mathematics, crystallography, etc.
Figure 2: Euclid Geometry
Convex Geometry
Absolute analysis methods are utilized to study the convex shapes in Euclidean space. It has applications in functional analysis and optimization in number theory.
Topology
It focuses on the qualities of space that persist in continuous mapping. Its application considers the compact size, correctness, coherency, filtration, function spaces, grills, grouping and clusters, interstellar space configurations, initial and final frameworks, metric areas, proximal continuity, proximity spaces, separation axioms, and homogeneous spaces.
Plane Geometry (Two-dimensional Geometry) (Two-dimensional Geometry)
Plane Geometry studies two-dimensional shapes, which you can sketch down on paper. These include lines, circles & triangles of two dimensions. Geometry on a flat surface, or “plane,” is called “two-dimensional” geometry.
Planar Geometry
Two-dimensional objects can be described by just two dimensions of space, like length and width. Each bit of shape depth needs to be addressed. Squares, triangles, rectangles, circles, and so on are all examples of plane figures.
Some key concepts in planar geometry are:
- Point
- Line
- Angles
Point
A point is a specific spot or location on a flat surface. A dot usually depicts them. A point is not an item but rather a location, which is an essential distinction. Remember that a point is only in location and has no dimensions.
Line
The line is straight (no curves), has no thickness, and stretches in both directions without end (infinitely). It is vital to notice that it is the combination of infinite points together to make a line. In geometry, we have vertical and horizontal lines corresponding to the y-axis and x-axis.
Angles in Geometry
In planar geometry, an angle is a figure produced by two rays that meet at a single point; this meeting point is known as the angle’s vertex.
Angles are further classified based on their values, such as acute (less than 90 degrees), right (equal to 90 degrees), obtuse (greater than 90 and less than 180 degrees), straight (equal to 180 degrees), and reflex (greater than 180 degrees and less than 360 dgrees), etc. We illustrate straight, acute, and right angles in the figure below.
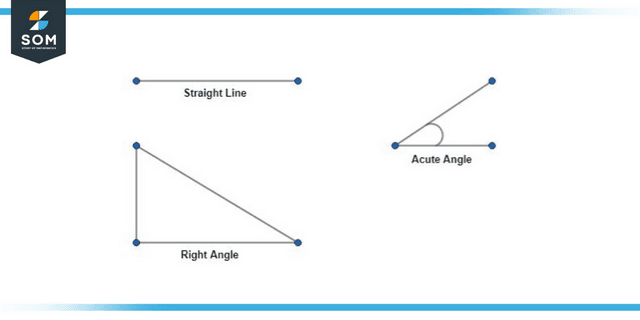
Figure 3: Angles in Geometry
Geometric Polygons
A closed polygonal network or loop is formed on the plane by a finite sequence of segments of straight lines that loop back on themselves.
Geometric Circle
There isn’t a more basic closed form than a circle. A circle is a closed contour (the path traced by a point that travels so that its distance from the center remains constant), with all its points being the same constant distance from a given point, the center.
Solid Geometry
Solid Geometry deals with 3-dimensional structures like cubic, prisms, cylinders & spheres. It deals with three qualities of the figure such as length, width, and height.
Terms in Solid Geometry
- Faces
- Edges
- Vertices
Solved Examples of Geometry-based Calculations
Example 1
An isosceles triangle has a perimeter of 30 cm, meaning that the triangle has two equal sides. The side AB = AC = X, and the remaining side is five more than AB and AC. Find the length of the non-similar side.
Solution
The summation of all three sides of the triangle is called perimeter; therefore, in this case, AB + AC + BC. As given in the statement, the similar sides of the isosceles triangle have a length, “X.”
Thus, AB + AC = X + X = 2X
The line BC has a length five more than the similar sides; thus, BC becomes 5 + X
The length of the line BC becomes:
30 = 2X + 5 + X
25 = 3X
25 / 3 = X
The length of BC becomes: (25 / 3) + 5 = (40 / 3)
Example 2
Find the distance of Point A (2, 6) from the origin (0,0).
Solution
Formula Applied:
\[ \sqrt{(X_2-X_1)+(Y_2-Y_1)} \]
\[ = \sqrt{(0-2) + (0-6)} \]
\[ = \sqrt{-2-6} \]
\[ = \sqrt{-8} = 2\sqrt{2i} \]
All images/mathematical drawings were created with GeoGebra.
