JUMP TO TOPIC
Half|Definition & Meaning
Definition
A half is one of the two equally split parts of a whole. For example, if you halved a cake to share it with your friend, you and your friend would get half of that cake. In fractions, a half is represented as 1/2.
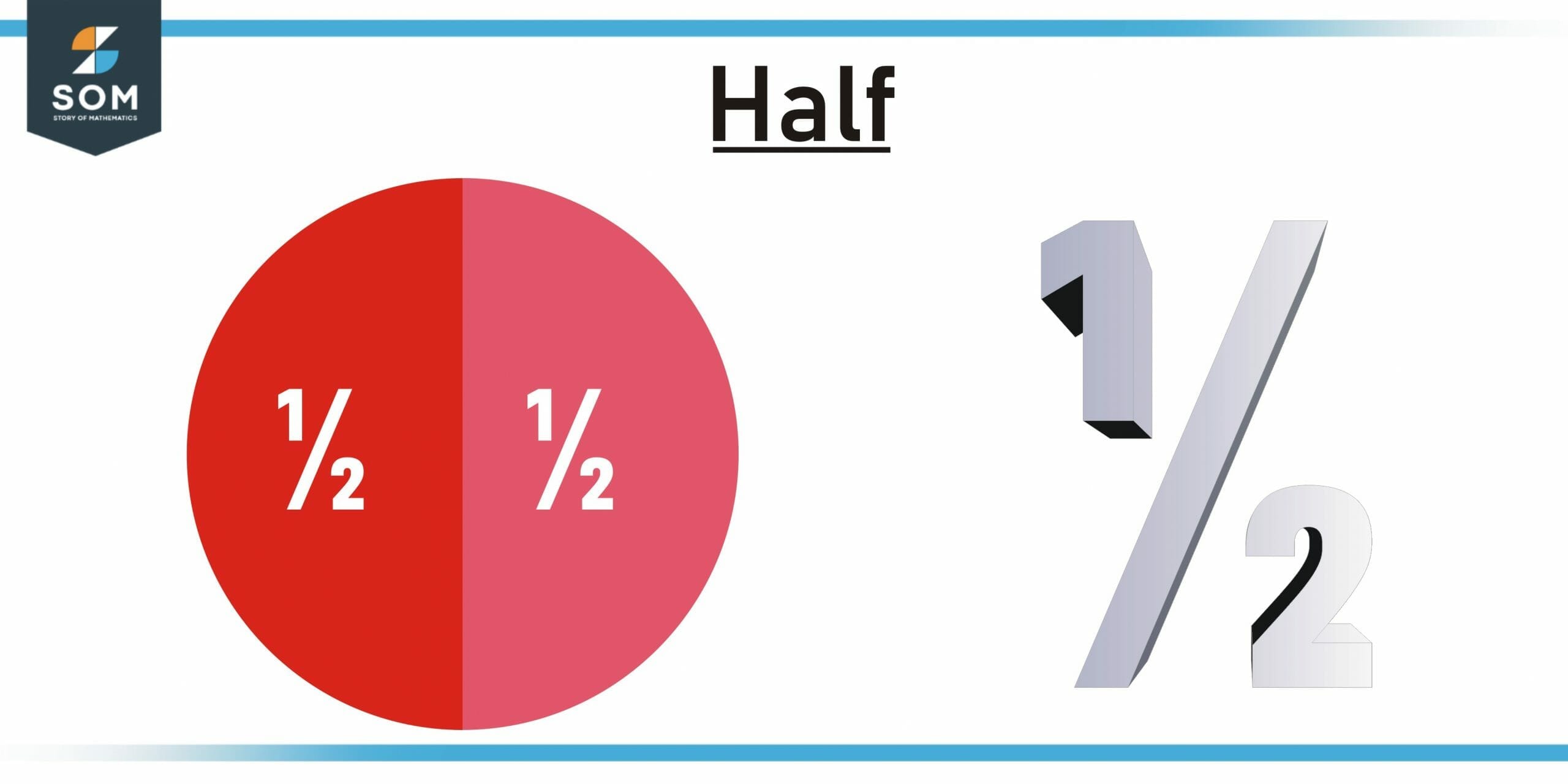
Figure 1 – Mathematical and Graphical Representation of Half
It is quite common to say that when a thing has been divided into two equal parts, it has been divided into two halves. So, in other words, by splitting a whole thing into two equal parts, you get two halves of that particular thing.
It is common for us to encounter a lot of examples of halves in the course of our daily lives. Oranges, watermelons, circles, and so on can all be split into halves. By dividing a number by 2, we can obtain half of it by dividing it into two equal parts.
How To Calculate Half of an Amount
Half of an amount can be found using this concept. The concept of halving can also be viewed as sharing equally between two people. If you would like to gain a better understanding of how to do this, one easy way would be to use materials that you can pick up, touch, and move around. As an example, let us look at the following.
Would It Be Possible for Two People to Share Four Cubes Equally?
You can use this method to learn how to halve numbers. It is the same as finding half of 4. If you are using physical cubes, you will be able to share one cube with each individual until you have run out of cubes. You will find out the answer by counting the number of cubes each person has.
To practice halving, you can use several objects lying around your home or school. For example, pencils, counters, sweets, etc.
Instead of using physical manipulatives to calculate half, a pencil, whiteboard, and paper can also be used. Would you like to find half of the 12 bananas?
Next, draw two circles to represent the two groups, and inside each circle, draw a banana until there are no more bananas left. In each group, how many bananas are there? The answer is there will be 6 bananas in each group.
How To Find Half of a Number
In mathematics, a half is equivalent to the fraction 1/2. Hence, we can divide a number by two to find half of it. Divide the total number by 2 by splitting it into two equal parts. Let us look at an example,
The half of 8 can be calculated by dividing it by 2. This calculation can be written as 8 ÷ 2. The answer to this calculation is 4. Adding 4+4 by itself and ensuring that it equals 8 confirms that this is the correct answer. Similarly, multiplying the answer by 2 (4 x 2) also equals 8, confirming our answer is correct.
How To Find Half of the Large Numbers
It is easier to do this when the number is smaller, but when the number is large, it can be a little bit tricky to divide the entire number by two. It would be easier to solve this if we partitioned the data. Splitting it into tens and ones makes it easier to half.
For example, let us take 98 as an example. It would be a bit tricky to divide by two in our heads and quickly half this number. Simply split the number 98 into tens and ones as following
The first thing to do is to split the tens in half (half of 90= 45). In the next step, we will divide the ones in half (half of 8), which equals four. To get the answer, you will need to add both numbers together. So, in this case, 49 is the answer. The partitioning strategy can also be used to halve very large numbers.

Figure 2 – A half apricot
Number Line Representation of Half
Fractions can be represented on a number line. Number lines have one whole distance between 0 and 1. By dividing the distance into two equal parts, we can get two halves.
Fractional Representation of Half
It is a part of a whole that makes up a fraction. Slices of cake are fractions, i.e., pieces of the whole cake when cut out. When it comes to fractions, half is equal to 1/2 of the total. In the fractional representation of half, the upper part (numerator) represents what we have, which is 1, whereas the lower part (denominator) contains the number in which the whole object has been divided, which is 2.
How To Represent Half in Decimal Form
0.5 is the decimal representation of one-half. A fractional representation of half is 1/2. As a result of simplifying 1/2, we get 0.5. When we multiply 0.5 by 0.5, we get 1, which proves that the sum of these two numbers equals one, which makes 1/2 a simplified number.
A Half’s Properties
Listed below are some of the properties of halves.
- In decimal form, the half value is written as 5.
- If you multiply a number by 1/2, then you can calculate half of it. Let us look at an example, half of 12 can be found by multiplying it by 1/2. 12×1/2 = 6
- Whenever you divide something in half, you always get two equal parts from one whole.
- A whole is formed by adding two halves together.
Real-life Solved Examples
Example 1
Rimsha, Maryam, and Rafia went to the grocery shop. They bought one dozen bananas. Maryam ate half of the bananas. Calculate how many bananas she used.
Solution

Figure 3 – Bananas divided equally
As we all know that one dozen bananas= 12
So, we can calculate it by dividing 12 by 2:
12/2 = 6 bananas
Example 2
Omer cut an apricot into two equal pieces and ate one of them. What fraction of apricot did he eat?
Solution
No of pieces the apricot was cut into= 2
No of pieces eaten = 1
Fraction of apricot eaten = No of pieces eaten/ Total no of pieces = 1/2
He ate 1/2 a fraction (or one-half) of an apricot.
All the mathematical images are generated using GeoGebra.
