Halve|Definition & Meaning

First things first, let’s define what we mean when we say “half.” Half consists of two portions that are equally divided from a whole. 

When we talk about halving shapes or actual things from the world around us, this becomes much simpler to grasp. Take, for instance, the fact that you are in possession of an entire Cake. In order to cut your cake into halves, first cut it into two pieces that are of equal size. Each individual serving is equivalent to one-half of the cake.

Figure 1 Graphical Depiction of whole cake into halve

Determining What Is Half of an Amount

Using this concept, we can determine what half of an amount is. Sharing something equally between two people is yet another way to think about the concept of halving.

Utilizing tangible objects that you can feel, pick up, and move around is a quick and simple method for gaining an understanding of how to carry out this process. Take, for instance, how is it possible for there to be an even split of 4 cubes between 2 people?

This is the same as determining what half of four is, and it is a more straightforward method for learning how to divide numbers in half.

If you are using physical cubes, you can divide them between two people by giving one cube to each of them until you run out of cubes. This can continue until there are no more cubes left. Simply tally up how many items are held by each individual, and you will have your answer.

In order to practice halving, you can do so with a variety of objects that are lying around the house or in the classroom. Why not use other things like books, pencils, or even tasty treats as counters? Keep in mind that to divide something in half means to do so equally between 2.

After you have gained some experience with the use of physical manipulatives, you can move on to calculating half using a whiteboard or a pencil and paper. Do you need to locate 10 Mangoes out of a total of 20? After that, draw two circles or rectangles to stand in for the two groups, and then draw one mango into each of the circles or rectangle, continuing until there are none more mangoes left. How many mangoes are there in each of the different groups?

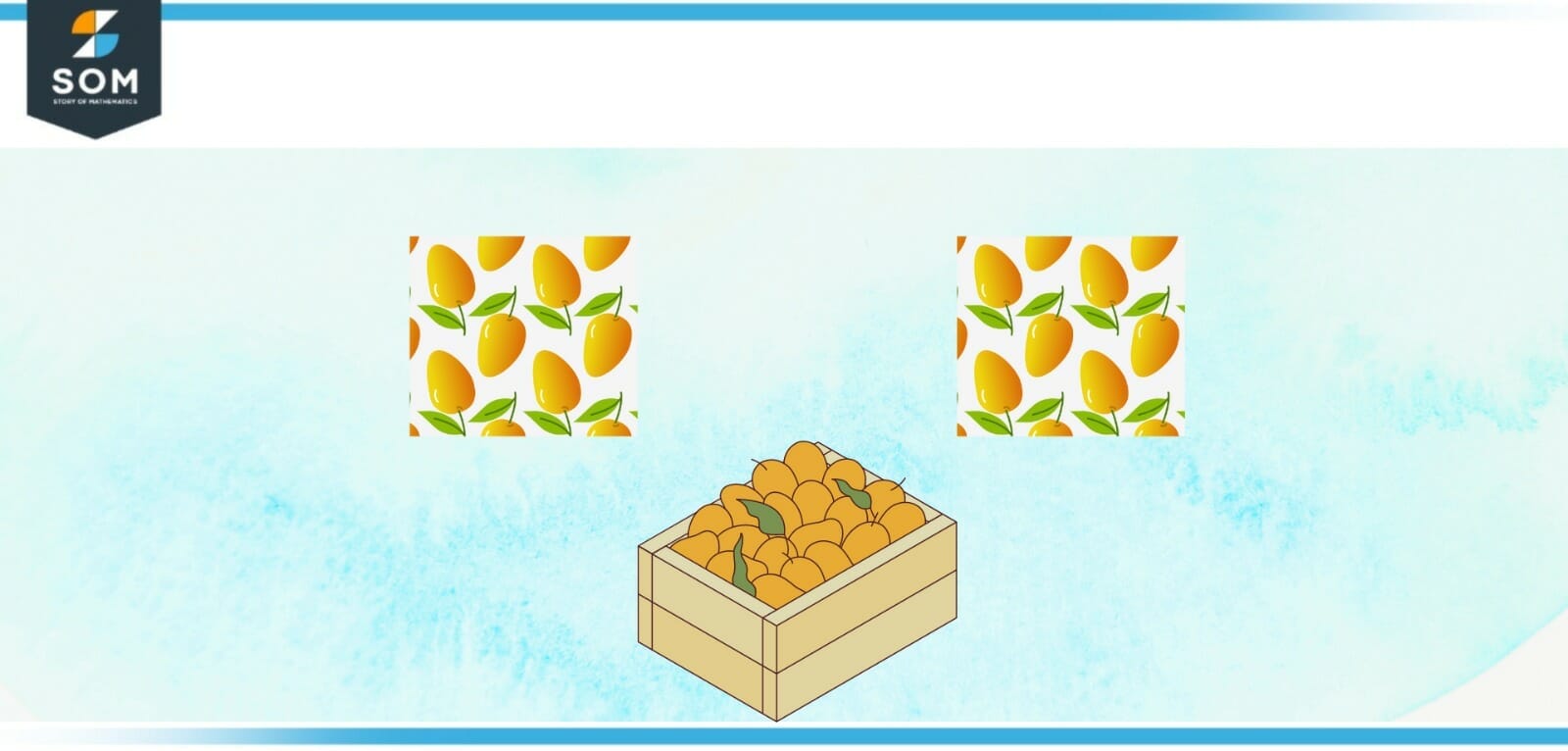
Figure 2 Example of Halving a Mangoes

How To Halve Numbers

A number can be halved by remembering that a half is equivalent to the fraction 1/2. This indicates that we can find one-half of a number by dividing that number by two. In order to perform a division by 2, first separate the total number into two halves that are identical. Take, for instance:

We can get the answer for half of six by dividing that number by two. This calculation can be written down as 6 divided by 2 or 6 $\div$ 2 or 6/2.

The answer that we get from this calculation is 3. We can verify that this is the correct answer by adding the numbers together (3+3) and ensuring that the resulting sum is equal to 6. It is, as expected.

In addition, we can confirm that our answer is correct by multiplying it by two, which brings us back to the number 6 (3 x 2). And with that, you’ve accomplished your goal of learning how to divide numbers by half.

How To Divide Large Numbers by Half

When we are dealing with smaller numbers, it is much simpler to perform this operation; however, when we are attempting to calculate half of a large number, it can be difficult to simply divide the entire number by 2.

By partitioning this problem, we can make it much easier to understand. At this point, we separate the number into tens and ones in order to make it simpler to divide it in half.

Let’s look at the number 96 as an illustration. It might be difficult for us to mentally cut this in half so quickly by dividing it by 2. Therefore, instead, the number should be broken down into tens and ones as follows:

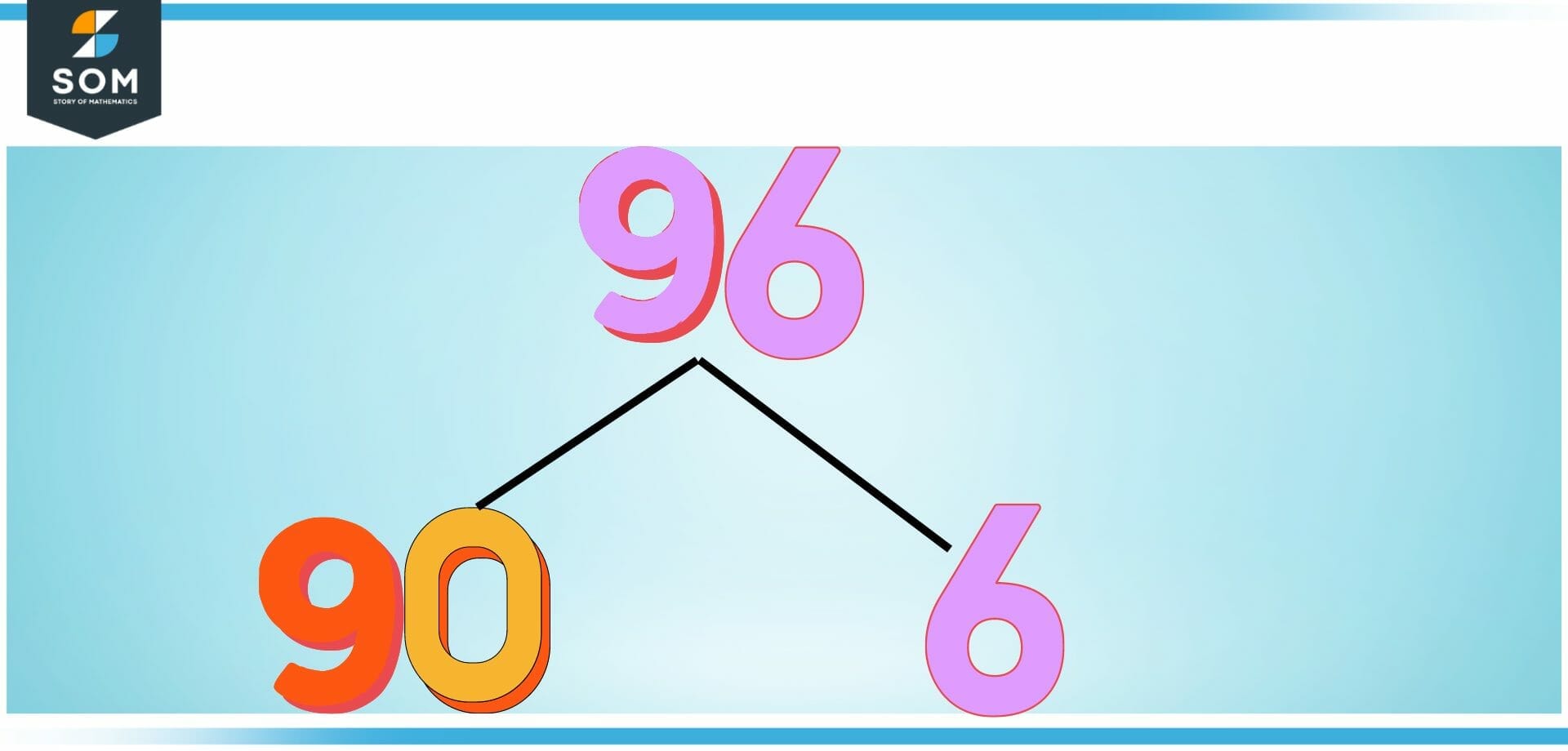
Figure 3 Graphical Depiction of how to Halve a number in tens and ones

First, let’s take 45, which is half of the tens (or half of 90). Then, one-half of the ones, which is three (one-half of six). Simply arrive at the answer by adding your two numbers together. In this particular scenario, the correct result is 48.

Using this method of partitioning, you can also cut in half even significantly larger numbers. Simply divide the total into thousands, hundreds, tens, and ones, and then proceed to calculate the result using the same method described in the previous paragraph.

Different Types of Halves

The idea of “halving” can be used in a variety of contexts, including mathematics and the real world, including the following:

1. Halving a quantity: Dividing a quantity into two equal parts is what is meant when we talk about halving a quantity.
2. Halving a line segment: Cutting a line segment in half means dividing it into two equal parts in order to create two line segments that are the same length.
3. Halving an angle: “Halving an angle” is the process of dividing an existing angle into two equal parts in order to create two new angles with the same degree of measurement.

These are the most common types of halving used in mathematics, and they have a number of applications in the real world, including geometry and construction, agriculture and horticulture, as well as cooking and baking.

Properties of Halves

Following are some properties of halves and halved objects:

• The concept of a whole thing broken down into two equal parts
• The symbol for half in decimal numbers is the fraction 0.5.
• We can obtain one-half of any number by dividing that number by 2.
• Putting together two halves results in a whole.

These properties are quite significant as they can help simplify the analysis of geometrical shapes and complex mathematical spaces.

Examples of How Halving Can Be Used in Real Life

The concept of halving has many real-world applications, including the following:

1. Geometry and Construction: The process of halving is utilized in geometry for the purpose of finding the midpoint of a line segment and dividing shapes into equal parts. In the building industry, this is utilized to measure and plot out equal distances for various construction projects.
2. Agriculture and Horticulture: In agriculture and horticulture, the term “halving” refers to the process of dividing land and plots into two equal parts for the purposes of planting and harvesting.
3. Cooking and Baking: In cooking and baking, the term “halving” refers to the process of dividing recipes into equal parts in order to create smaller portions or halving ingredients in order to create a smaller serving size.

These are just some of the many applications of halving that can be found in real-world settings. The mathematical operation of halving is a fundamental concept that has practical applications in a wide variety of fields, including design, engineering, and finance, amongst others.

Important Concepts

The division by two is a fundamental mathematical operation that has a number of applications in the real world. In geometry, construction, agriculture, horticulture, cooking, and baking, halving is a useful tool that is used to divide quantities, line segments, and angles into equal parts. In addition, halving is used to divide quantities into half of the original size.

The process of halving offers a straightforward method for partitioning complicated issues into more manageable chunks and enables calculations that are both more precise and time-effective. As a result of the fact that it is a fundamental concept in fractions as well as division, it is an essential tool for students learning mathematics.

The idea of halving is an important one in mathematics, and it can be used to solve problems in a wide variety of other disciplines as well. The fact that it can break complicated issues down into more manageable chunks and offer solutions that are both more accurate and more time-effective is the primary reason for its significance.

Example

Consider the following scenario: a person has 10 pieces of chocolate and is asked to give exactly half of each piece to a friend. I was wondering how many chocolates they would have to give away.

Solution

Because we already know how to do the calculation, we can determine the value of half by dividing the total by 2. If there are a total of 10 pieces of chocolate, then 50 percent of that would be 5 since 10 divided by 2 is equal to 5. The individual would present their close friend with exactly five chocolates.

All images/mathematical drawings were created with GeoGebra.

Half Definition < Glossary Index > Hect Definition