JUMP TO TOPIC
Height|Definition & Meaning
Definition
Height of a geometrical shape represents the vertical distance from the base to its opposite vertex. Since the distance must be measured vertically, the line joining the base and the vertex must be perpendicular (angle of 90$^\circ$).
Height is usually defined for polygons only. Polygons are geometrical shapes that have 3 or more sides. A triangle is the simplest possible polygon.
Height of Triangle
There are different types of triangles, each of which have different procedures of finding height.
Height of Right Angle Triangle
A right-angle triangle is a special triangle where one of the interior angles is 90$^\circ$. The three sides of the right angle triangles are Base, Perpendicular, and Hypotenuse as shown in the figure below.
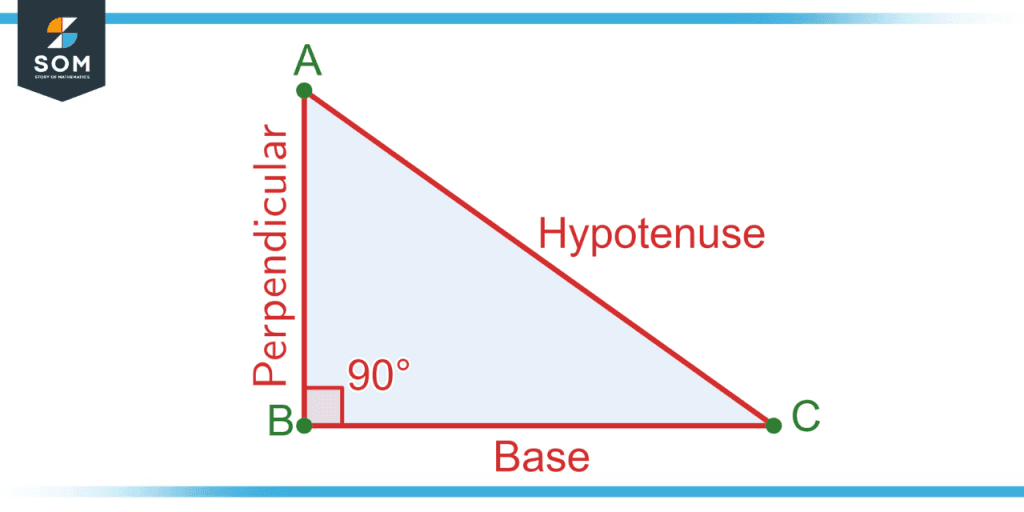
Figure 1 – A right-angle triangle with three sides.
It can be seen that the perpendicular represents the distance from the base of the triangle to its vertex. Hence, in the case of a right-angle triangle, the height is given by perpendicular. The lengths of the right angle triangle’s three sides are related by the Pythagoras Theorem given by:
Hypotenuse2 = Base2 + Perpendicular2
Hence, by knowing the length of any two sides we can compute the length of the third unknown side through the use of Pythagoras’ theorem.
Height of Other Triangles
In triangles with no right angle, the height is computed by joining the base and the opposite vertex through a perpendicular. This perpendicular then represents the height of that triangle.
In the following triangle ABC, BC is the base of the triangle. The height is found by joining the base BC to the opposite vertex A through a perpendicular AD. Thus, AD is the height of the triangle.
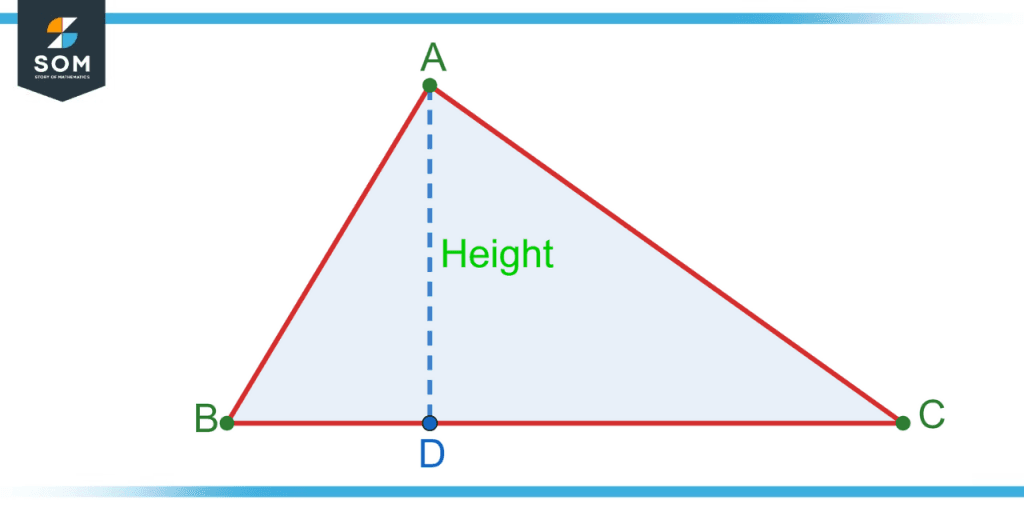
Figure 2 – Height of triangle obtained by joining base to opposite vertex through a perpendicular.
The area of a triangle directly depends on its height:
Area = (1/2) * b * h
Where ‘b’ and ‘h’ respectively represent the length of the base and the height of the triangle.
Height of Parallelogram
A parallelogram is a four-sided polygon consisting of a pair of parallel sides equal in length. There are three types of parallelograms: Square, Rectangle, and Rombous.
Height of Square
A parallelogram in which all four sides and angles are equal is called a square. All the angles are right angles. Since all the sides are equal, the height of square is the same as length of any side.
Height of Rectangle
A parallelogram in which both pairs of opposite sides are equal, and all angles are equal, is a rectangle. All the angles are right angles. The dimensions of the rectangle are represented by its width and height. The vertical dimension is the height, and the horizontal dimension is the length.
Height of Rhombus
A type of parallelogram in which all four sides and a pair of opposite angles are equal is called a rhombus. In the case of Rhombus, height is not directly given and is computed by joining the base to the opposite vertex through a perpendicular.
Height of Trapezium
A trapezium is a four-sided polygon with a pair of parallel sides. The bases in this context are the parallel sides. The height of the trapezium is the vertical distance between the two bases and is obtained by joining them through a perpendicular line.
In the trapezium ABCD shown below, the two parallel sides are AD and BC. These sides also form the bases of the trapezium. The perpendicular distance between these bases represents the height of the trapezium and is shown by AE in the figure.
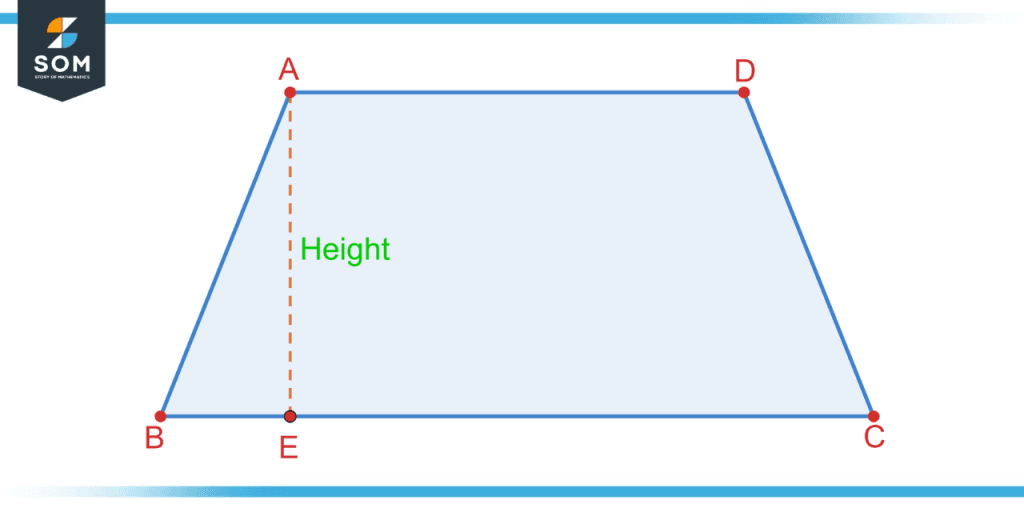
Figure 3 – Height of trapezium ABCD is given by AE.
Height of the trapezium is required to compute its area:
Area = 1/2 * (Sum of parallel sides) * height
A Few Examples of Calculating Heights of Polygons
Example 1
A triangle ABC with two sides length is shown. Compute the height of the triangle.
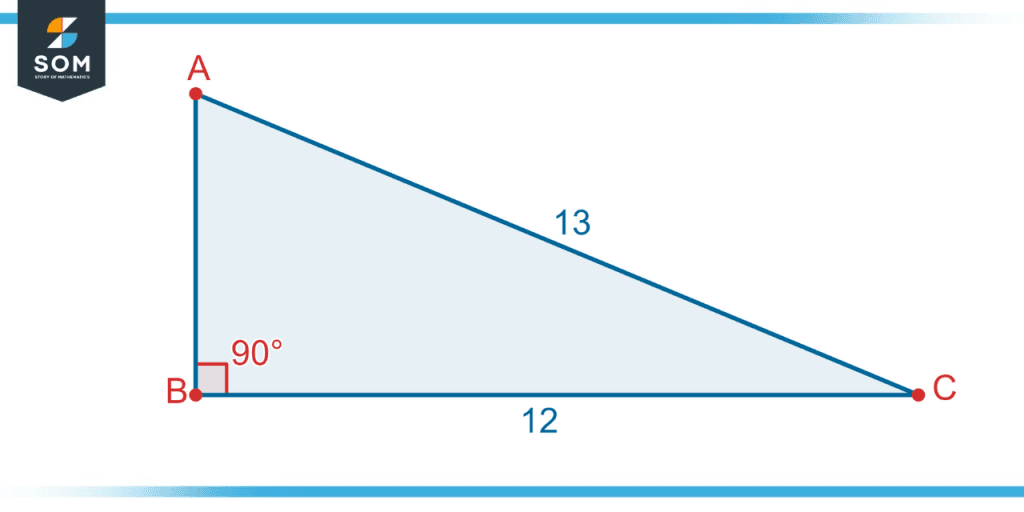
Figure 4 – A right triangle with two known sides and one unknown side.
Solution
In the given triangle ABC, note that there is a 90-degree angle. This means that the triangle is a right-angle triangle. As discussed earlier, the height of right angle triangle is given by the perpendicular of the triangle. In the given triangle, two sides’ lengths are given. The given sides’ length are:
Base = 12 and Hypotenuse = 13
Using the Pythagoras theorem:
132 = 122 + Perpendicular2
Computing the squares gives:
169 = 144 + Perpendicular2
Solving the equation for perpendicular produces:
Perpendicular = $\mathsf{\sqrt{25}}$
And thus, the length of the perpendicular is:
Perpendicular = 5 units
Hence, the height of the given triangle is 5 units.
Example 2
A trapezium has an area of 35 square units. The two parallel sides are 6 and 8 units. Calculate the height of the trapezium.
Solution
Note that the two parallel sides of the trapezium are called its bases. Thus, the lengths of the bases of the trapezium are given as 6 and 8 units. Recall that the area of the trapezium is given by:
Area = (1/2) * (Sum of parallel sides) * height
Substitute the given value of area and lengths of parallel sides:
35 = (1/2) * (6 + 8) * height
35 = 7 * height
Solve the equation to compute the height:
Height = 5 units
Hence, the height of the given trapezium is 5 units.
Example 3
An equilateral triangle has a base of length 6 units. Calculate the height of the triangle.
Solution
Consider an equilateral triangle ABC as shown in the figure. The height of the triangle will be the perpendicular distance from base BC to vertex A. Thus, AD represents the height of the triangle.
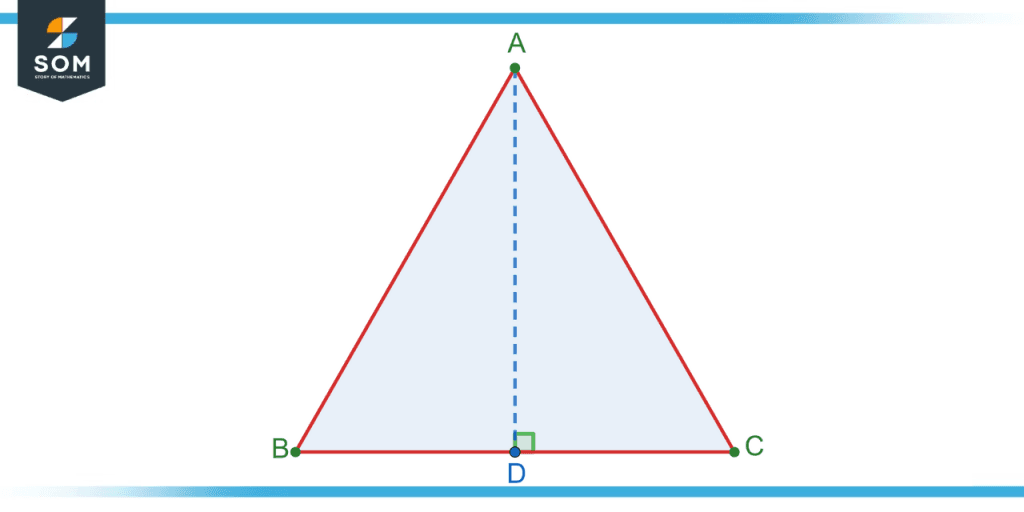
Figure 5 – An equilateral triangle ABC with height AD.
Note that the lengths of all sides of an equilateral triangle are equal. This means that the length of AC is also 6 units. Also, note that AD is a perpendicular bisector to the base BC. Thus, the length of DC is 3 units – half of the length of BC.
Now consider the right angle triangle ADC. The length of two sides AC and DC is known and the length of the third side AD is to be found which represents the perpendicular of the triangle.
Using Pythagoras’ theorem, the equation will be:
62 = 32 + Perpendicular2
Solving the equation results in:
Perpendicular = 3$\mathsf{\sqrt{3}}$
Thus, the height of the equilateral triangle is $\mathsf{3\sqrt{3}}$ units.
All images/mathematical drawings were created with GeoGebra.
