Horizontal Flip|Definition & Meaning

Conceptual Illustration of Horizontal Flip

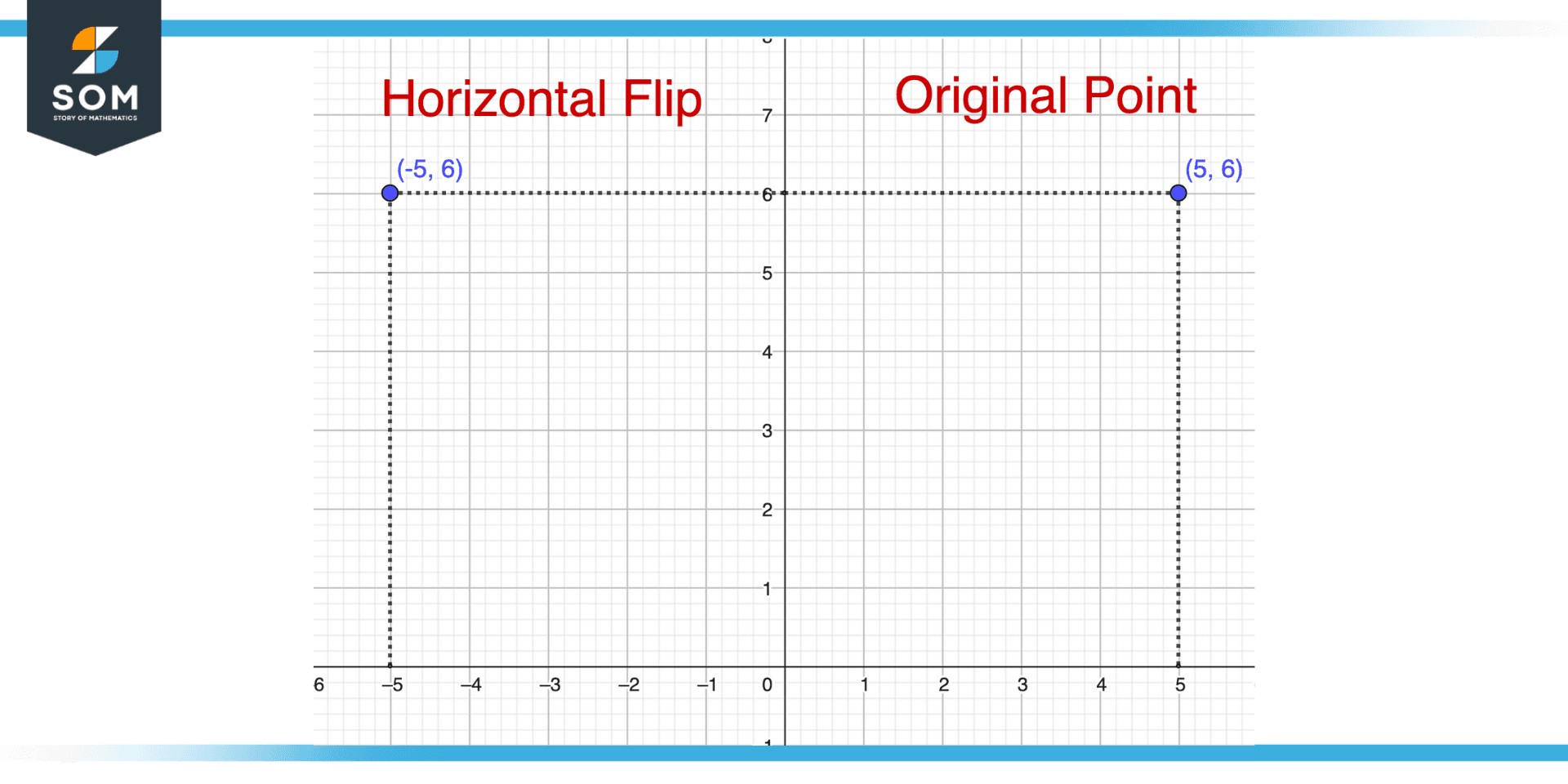
Figure 1 – Illustration of the horizontal flip of a point with x-coordinate 5 and y-coordinate 6, i.e., (5, 6).

Consider the following example. Take the coordinates of a point, P, and imagine it has these coordinates (5, 6). Our goal is to find its reflection along the y-axis if we want to flip it horizontally. This is accomplished simply by changing the sign of the x-coordinate (from 5 to -5) and the y-coordinate of the point (6 in this case). For a horizontally flipped point, we get (-5, 6) as its new coordinates.

In general, the coordinates of a point P with respect to the x and y axes are represented by (x, y), where x is the distance of the point from the y-axis, and y is the distance of the point from the x-axis. When we horizontally flip a point, we take its y-coordinate and change the sign of its x-coordinate. This gives us the new coordinates (-x, y) for the flipped point.

Horizontal Flip of Person in Mirror

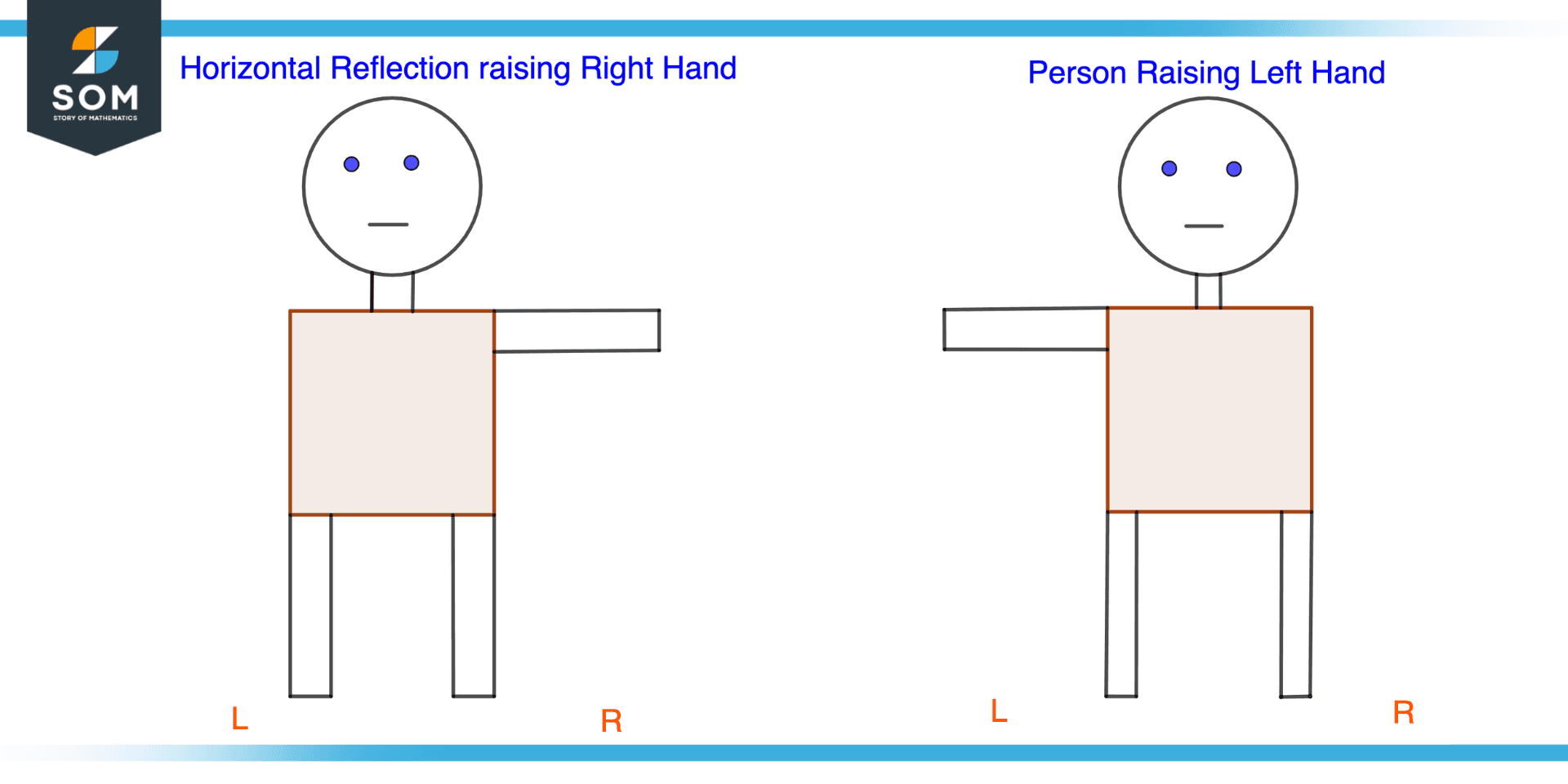
Figure 2 – Horizontal reflection of a person raising their left hand in a mirror

Imagine standing in front of a mirror and watching your reflection in order to visualize a horizontal flip reflection. In the event that you raised your left hand, your reflection would raise its right hand. The mirror reflects you horizontally, flipping left and right without flipping up and down.

Horizontal Flip in Arts

Reflections on the horizontal plane are commonly used in art to create symmetry and balance. An artist could, for instance, paint a painting with a tree on one side and its reflection on the other side. Flipping the tree’s original image horizontally would result in the reflection. By doing so, the painting would appear balanced and harmonious.

Properties of Horizontal Flip 

A horizontal flip has the following properties:

• It preserves distances between points because it is an isometry. Accordingly, any distance between any two points of the original shape will match any space between the corresponding points of the flipped shape.
• Basically, it is its own inverse or involution. The original shape will be returned if you flip a shape horizontally and then flip it again.
• On the shape, it reverses the order of the points. When a line has A, B, and C at the points, then when it is flipped, it will have C, B, and A at the points.
• By doing this, all points on the shape are given a new sign for their x-coordinates. Flipping occurs as a result of this.
• A point on the shape will still maintain its y-coordinates. By flipping the shape, points are not affected in their vertical position.

Horizontal Flip of a Point

To find the horizontal flip of a point, you can use the following steps:

1. You need to identify the x-coordinate of the point. The horizontal axis shows this value.
2. Take the x-coordinate and multiply it by -1. By doing this, the x-coordinate is flipped horizontally, effectively changing its sign.
3. As a result, the original point will be horizontally flipped. For instance, if the original point is (1, 2), the horizontal flip will be (-1, 2).

Throughout these steps, the origin (0, 0) is assumed to be the center of the flip. Adding or subtracting the distance from the origin to the flip center will adjust the x-coordinate if the flip center is offset from the origin (i.e., the flip is not about the origin as initially assumed).

Horizontal Flip using Transformation Matrix

1. Use a 2D vector representation of the x and y coordinates of the point in the original image. For example\[ x=\begin{bmatrix} x \\ y \end{bmatrix} \]
2. In order to flip the image horizontally, define the transformation matrix. This matrix can be defined as\[ T=\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \]
3. Using the matrix multiplication operation, multiply the coordinates of the point by the transformation matrix. The point in the flipped image will now have its new coordinates. For example x’ = T * x.\[ x’=\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\]
4. Multiplying x by a transformation matrix will give the point in the flipped image its new coordinates, x‘. A point in a flipped image can be located using these coordinates.\[ x’=\begin{bmatrix} -x \\ y \end{bmatrix} \]

Horizontal Flip of a Geometric Shape

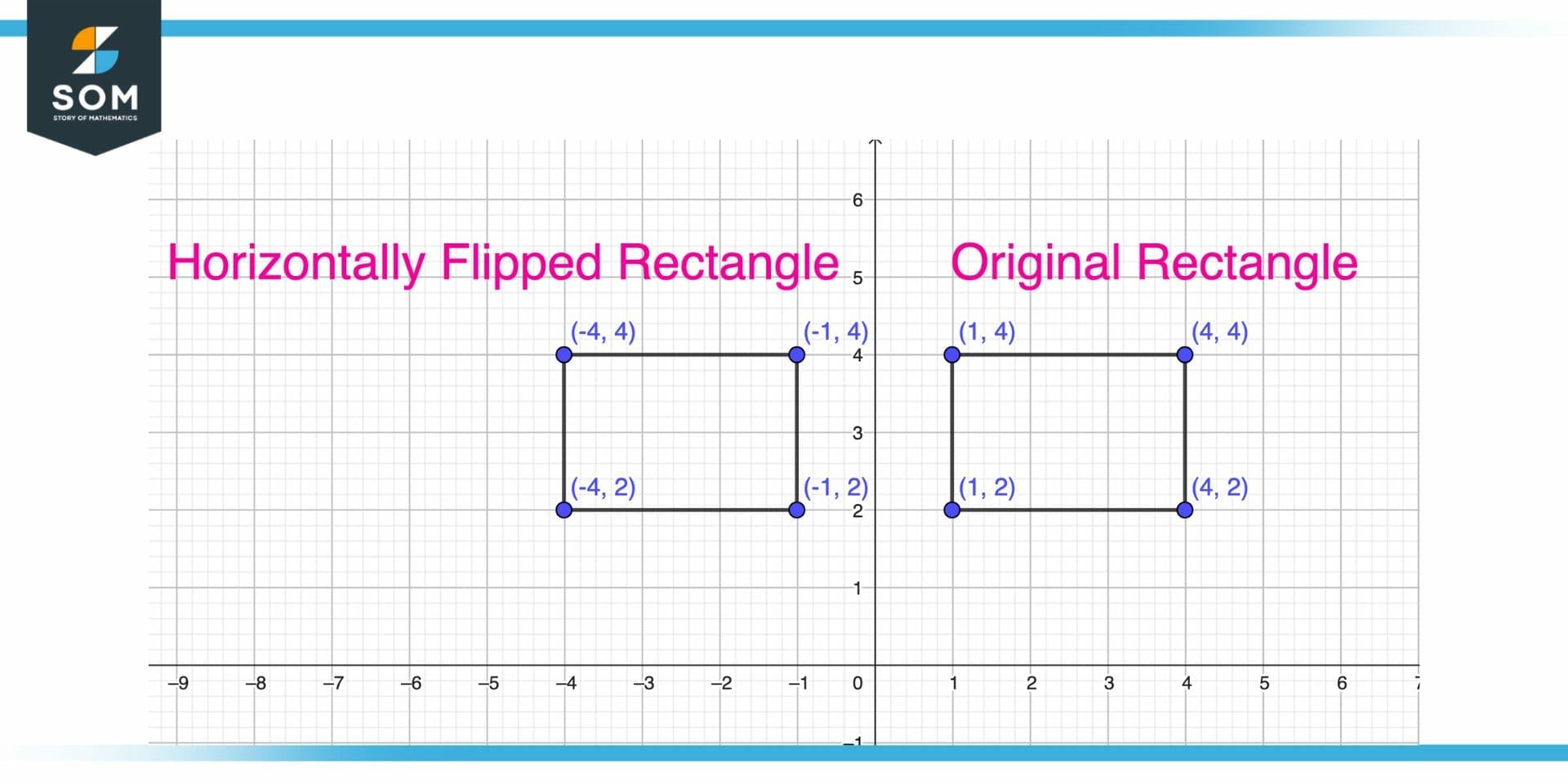
Figure 3 – Horizontally flipped rectangle

To find the horizontal flip of any geometric shape like a rectangle, square, parallelogram, or polygon we can use the following steps:

1. Identify the coordinates of the corners of the geometric shape. You will need the x-coordinates and y-coordinates of each corner.
2. Multiply the x-coordinates of all corners by -1. This will change the sign of the x-coordinates, effectively flipping the geometric shape horizontally.
3. The resulting coordinates will be the corners of the horizontal flip of the original geometric shape. For example, if the original rectangle has corners at (x1, y1), (x2, y2), (x3, y3), and (x4, y4), the horizontal flip will have corners at (-x1, y1), (-x2, y2), (-x3, y3), and (-x4, y4).Illustration is shown above.

Solved Example

You are given a triangle having three corners (3.5, 5), (2, 2), and (5, 2). Compute the Horizontal Flip of the triangle.

Solution

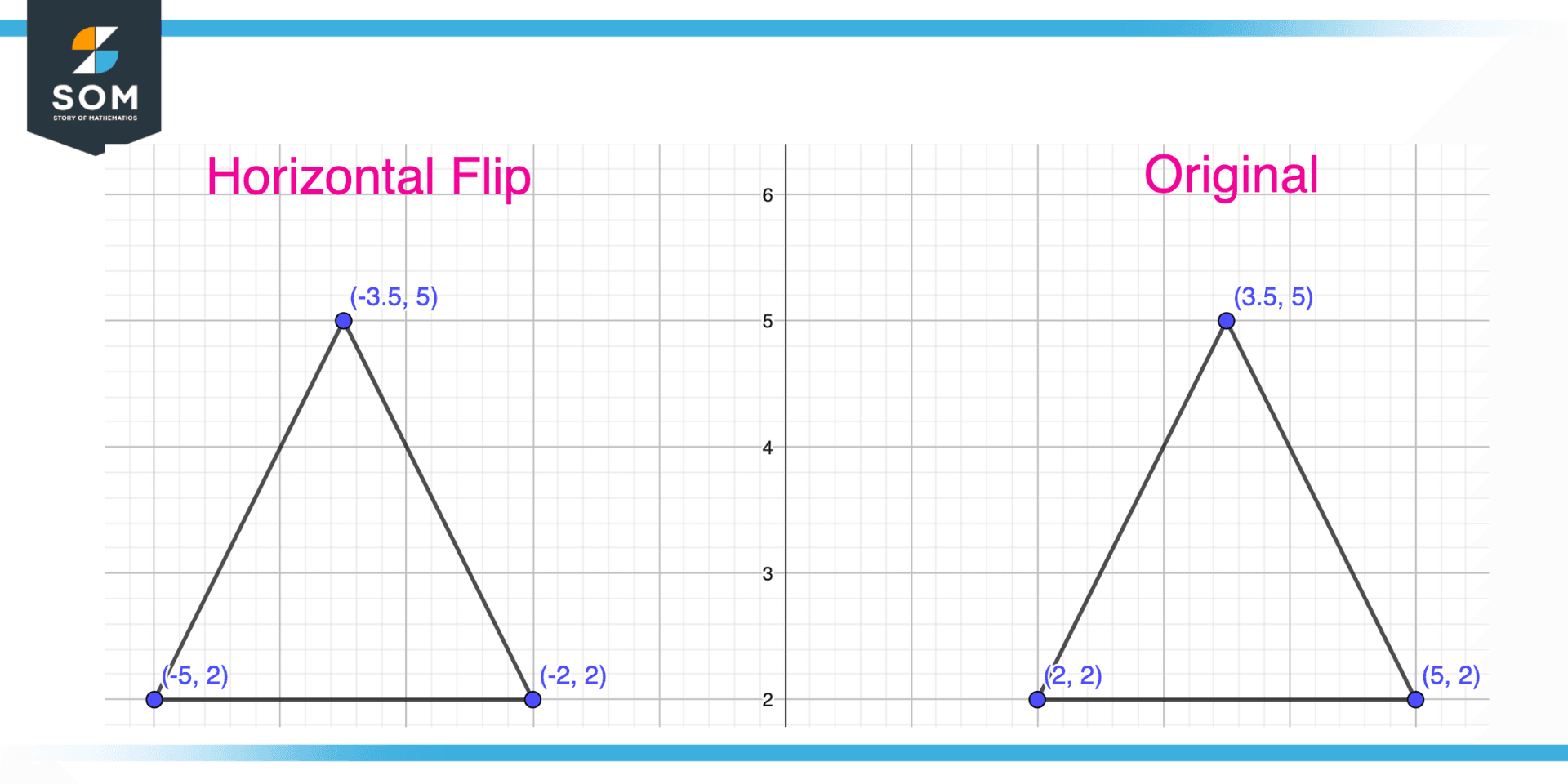
Figure 4 – Example of horizontally flipping a triangle

The process of finding the horizontal flip of a triangle involves first identifying the coordinates of the triangle’s vertices. This information is typically given in the form of a list of x-coordinates and a separate list of y-coordinates. In this example, the triangle has vertices at (3.5, 5), (2, 2), and (5, 2), the coordinates would be (3.5, 2, 5) for the x-coordinates and (5, 2, 2) for the y-coordinates.

Next, the x-coordinates of each vertex are multiplied by -1. This changes the sign of the x-coordinates, effectively flipping the triangle horizontally. The resulting coordinates are the vertices of the horizontal flip of the original triangle. In the example above, the horizontal flip would have vertices at (-3.5, -2, -5) for the x-coordinates and (5, 2, 2) for the y-coordinates.

All mathematical drawings and images were created with GeoGebra.

Histogram Definition < Glossary Index > Hour Definition