Hypothesis|Definition & Meaning

In mathematics, any statement or equation that describes some relationship between certain variables can be termed as hypothesis if it is consistent with some initial supporting data or information, however, its yet to be proven true or false by some definite and trustworthy experiment or mathematical law. 

Following example illustrates one such hypothesis to shed some light on this very fundamental concept which is often used in different areas of mathematics.

Figure 1: Example of Hypothesis

Here we have considered an example of a young startup company that manufactures state of the art batteries. The hypothesis or the claim of the company is that their batteries have a mean life of more than 1000 hours. Now its very easy to understand that they can prove their claim on some testing experiment in their lab.

However, the statement can only be proven if and only if at least one batch of their production batteries have actually been deployed in the real world for more than 1000 hours. After 1000 hours, data needs to be collected and it needs to be seen what is the probability of this statement being true.

The following paragraphs further explain this concept.

Explanation of Hypothesis

As explained with the help of an example earlier, a hypothesis in mathematics is an untested claim that is backed up by all the known data or some other discoveries or some weak experiments.

In any mathematical discovery, we first start by assuming something or some relationship . This supposed statement is called a supposition. A supposition, however, becomes a hypothesis when it is supported by all available data and a large number of contradictory findings.

The hypothesis is an important part of the scientific method that is widely known today for making new discoveries. The field of mathematics inherited this process. Following figure shows this cycle as a graphic:

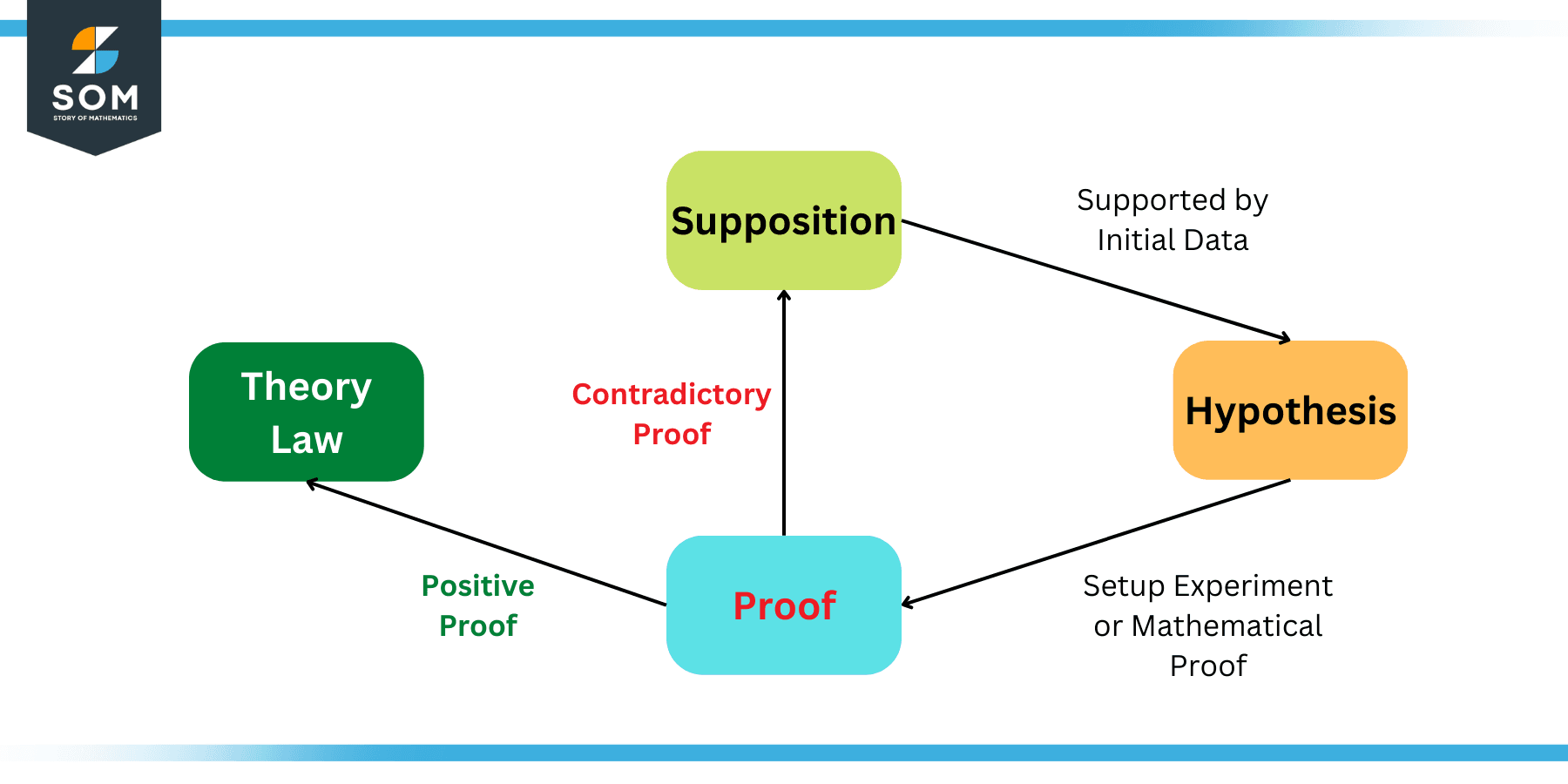
Figure 2: Role of Hypothesis in the Scientific Method 

The above figure shows a simplified version of the scientific method. It shows that whenever a supposition is supported by some data, its termed as hypothesis. Once a hypothesis is proven by some well known and widely acceptable experiment or proof, its becomes a law. If the hypothesis is rejected by some contradictory results then the supposition is changed and the cycle continues.

Lets try to understand the scientific method and the hypothesis concept with the help of an example. Lets say that a teacher wanted to analyze the relationship between the students performance in a certain subject, lets call it A, based on whether or not they studied a minor course, lets call it B.

Now the teacher puts forth a supposition that the students taking the course B prior to course A must perform better in the latter due to the obvious linkages in the key concepts. Due to this linkage, this supposition can be termed as a hypothesis.

However to test the hypothesis, the teacher has to collect data from all of his/her students such that he/she knows which students have taken course B and which ones haven’t. Then at the end of the semester, the performance of the students must be measured and compared with their course B enrollments.

If the students that took course B prior to course A perform better, then the hypothesis concludes successful. Otherwise, the supposition may need revision.

The following figure explains this problem graphically.

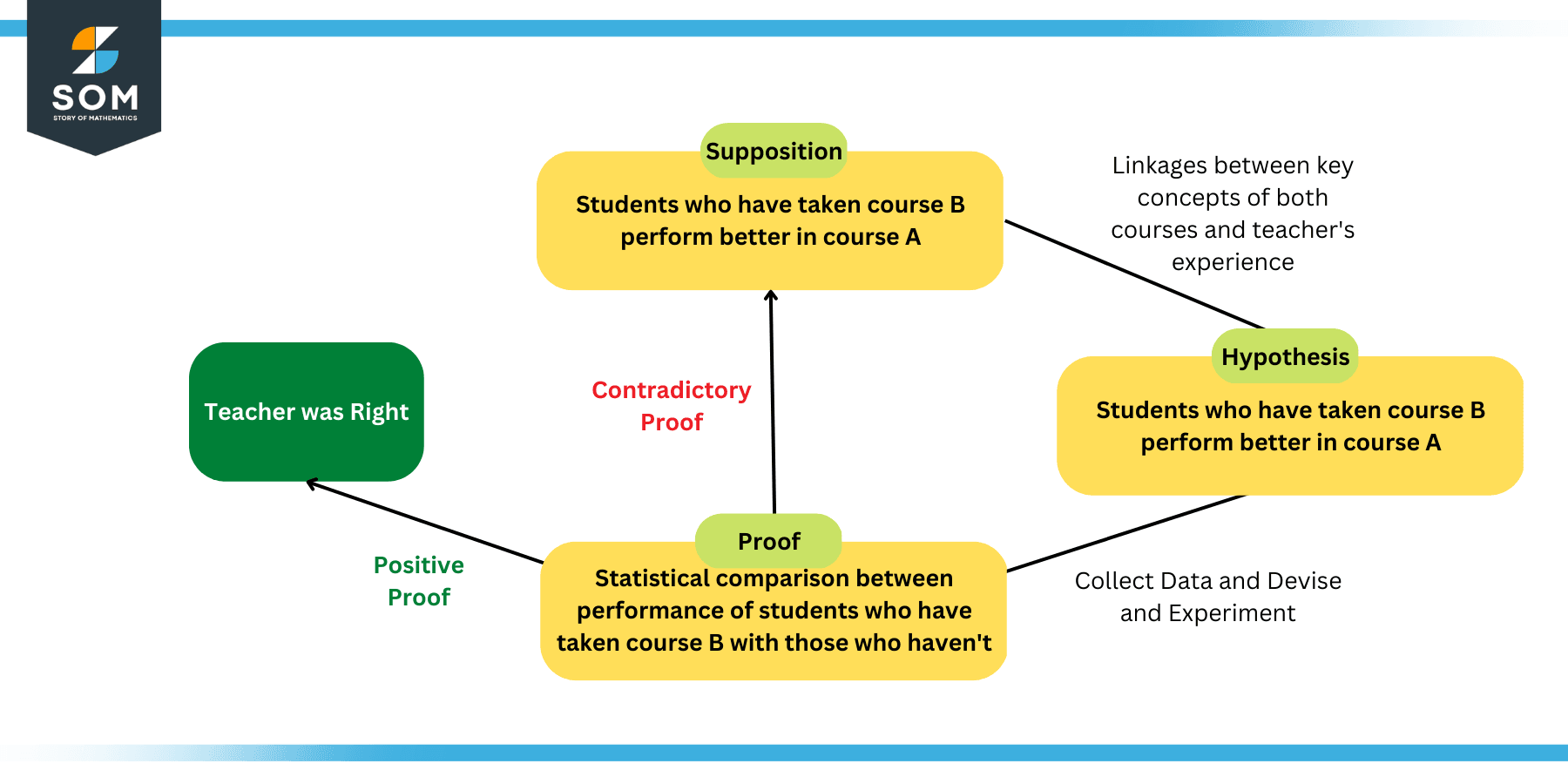
Figure 3: Teacher and Course Example of Hypothesis

Important Terms Related to Hypothesis

To further elaborate the concept of hypothesis, we first need to understand a few key terms that are widely used in this area such as conjecture, contradiction and some special types of hypothesis (simple, complex, null, alternative, empirical, statistical). These terms are briefly explained below:

Conjecture

A conjecture is a term used to describe a mathematical assertion that has notbeenproved. While testing may occasionally turn up millions of examples in favour of a conjecture, most experts in the area will typically only accept a proof. In mathematics, this term is synonymous to the term hypothesis.

Contradiction

In mathematics, a contradiction occurs if the results of an experiment or proof are against some hypothesis. In other words, a contradiction discredits a hypothesis.

Simple Hypothesis

A simple hypothesis is such a type of hypothesis that claims there is a correlation between two variables. The first is known as a dependent variable while the second is known as an independent variable.

Complex Hypothesis

A complex hypothesis is such a type of hypothesis that claims there is a correlation between more than two variables. Both the dependent and independent variables in this hypothesis may be more than one in numbers.

Null Hypothesis

A null hypothesis, usually denoted by H0, is such a type of hypothesis that claims there is no statistical relationship and significance between two sets of observed data and measured occurrences for each set of defined, single observable variables. In short the variables are independent.

Alternative Hypothesis

An alternative hypothesis, usually denoted by H1 or Ha, is such a type of hypothesis where the variables may be statistically influenced by some unknown factors or variables. In short the variables are dependent on some unknown phenomena.

Empirical Hypothesis

An Empirical hypothesis is such a type of hypothesis that is built on top of some empirical data or experiment or formulation.

Statistical Hypothesis

A statistical hypothesis is such a type of hypothesis that is built on top of some statistical data or experiment or formulation. It may be logical or illogical in nature.

Special Example of Hypothesis

According to the Riemann hypothesis, only negative even integers and complex numbers with real part 1/2 have zeros in the Riemann zeta function. It is regarded by many as the most significant open issue in pure mathematics.

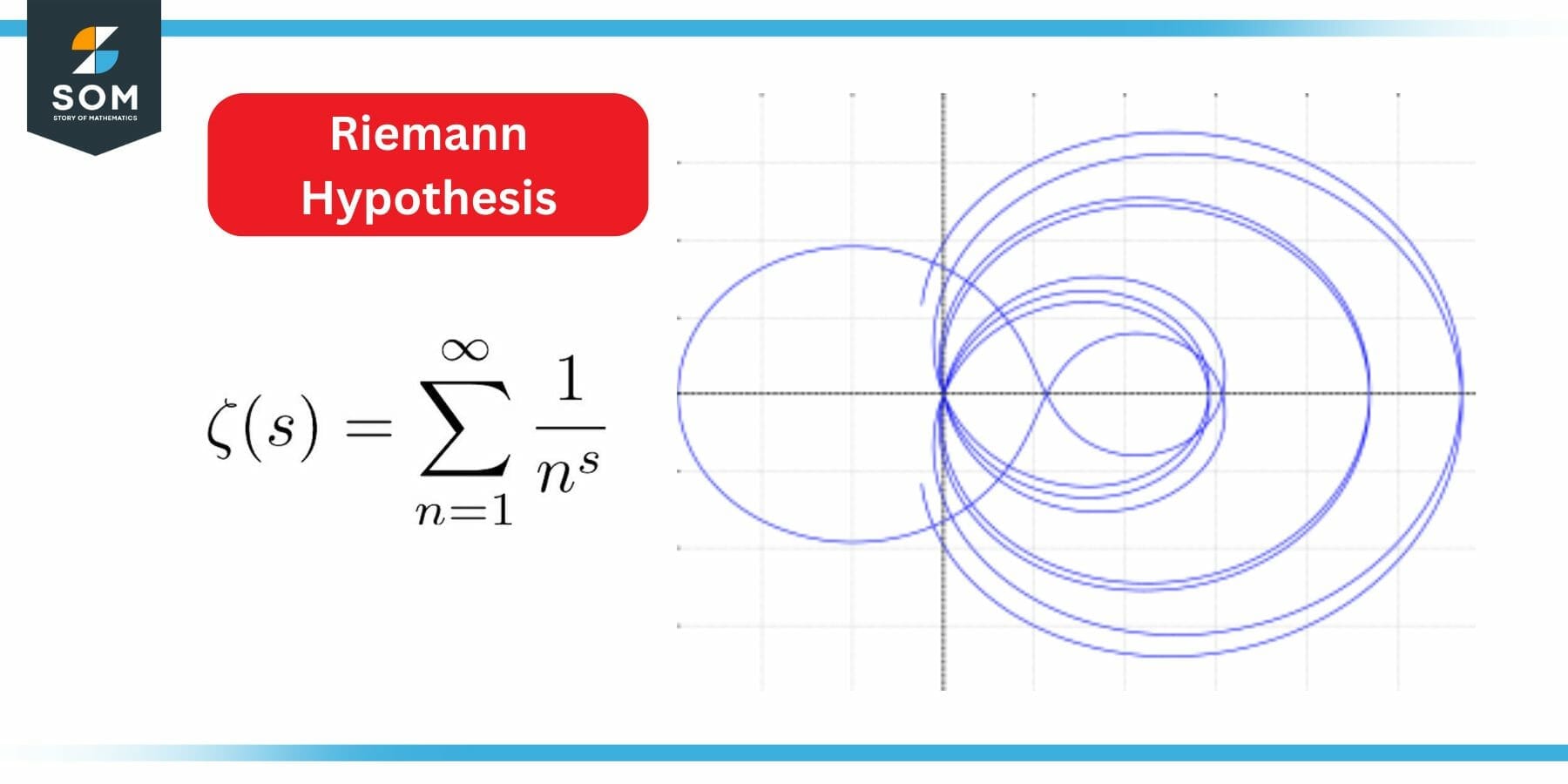
Figure 4: Riemann Hypothesis

The Riemann hypothesis is the most well-known mathematical conjecture, and it has been the subject of innumerable proof efforts.

Numerical Examples

Identify the conclusions and hypothesis in the following given statements. Also state if the conclusion supports the hypothesis or not.

Part (a): If 30x = 30, then x = 1

Part (b): if 10x + 2 = 50, then x = 24

Solution Part (a)

Hypothesis: 30x = 30

Conclusion: x = 10

Supports Hypothesis: Yes

Solution Part (b)

Hypothesis: 10x + 2 = 50

Conclusion: x = 24

Supports Hypothesis: Yes

All images/mathematical drawings were created with GeoGebra.

Hour Hand Definition < Glossary Index > Identity Definition