Identity|Definition & Meaning

No matter the number selected for “a,” x/2 = 0.5x is true, for instance. 

An equation valid regardless of the value selected for its variables is said to have an identity. Algebraic expressions can be rearranged or simplified using them. According to the definition, two identities are interchangeable. Therefore, we are always free to switch between them.

Figure 1 below shows the identity between 2 sides.

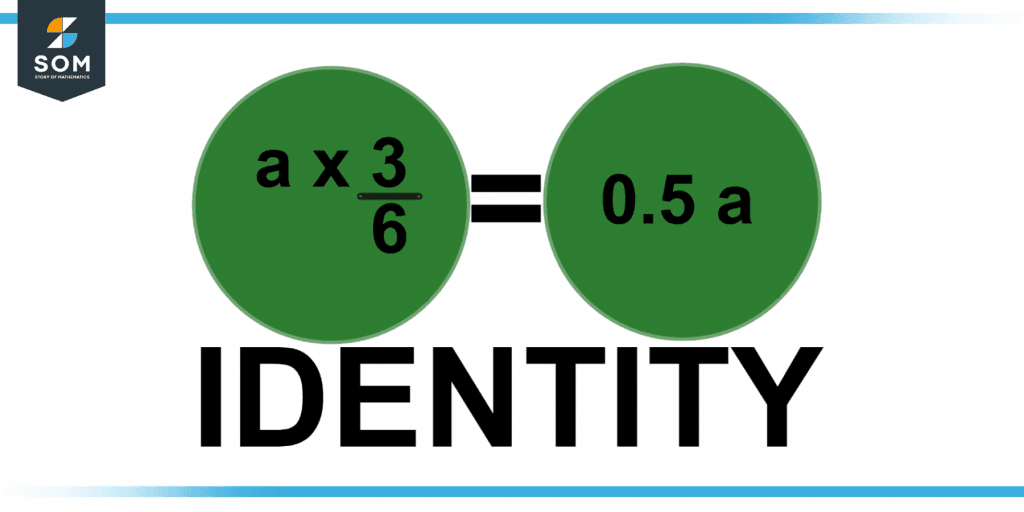
Figure 1 – Representation of identities.

Identity Function

An identity or identity map is another name for the identity function. A polynomial function is exemplified by the identity function. It is a particular kind of linear function where the result and input are identical. For an identity function, the domain values are the same as the range values. When a function yields the same result as the output that served as its input, it is known as an identity function. 

A function known as an identity equation is one in which every member in a set B represents itself as another element that is $g(b)=b \ \forall \ b \ \epsilon \ B$. 

It is therefore represented by “I” and has the format g(x) = x. Because the output of an item in the domain and the result in the range are the same, this function is known as an identity function. An identity function, therefore, corresponds to each precise figure to itself. An identity function has the same input and output. Since the which was before and the picture are identical, identity functions are simple to recognize.

Figure 2 below shows the identity function between two sets of elements.

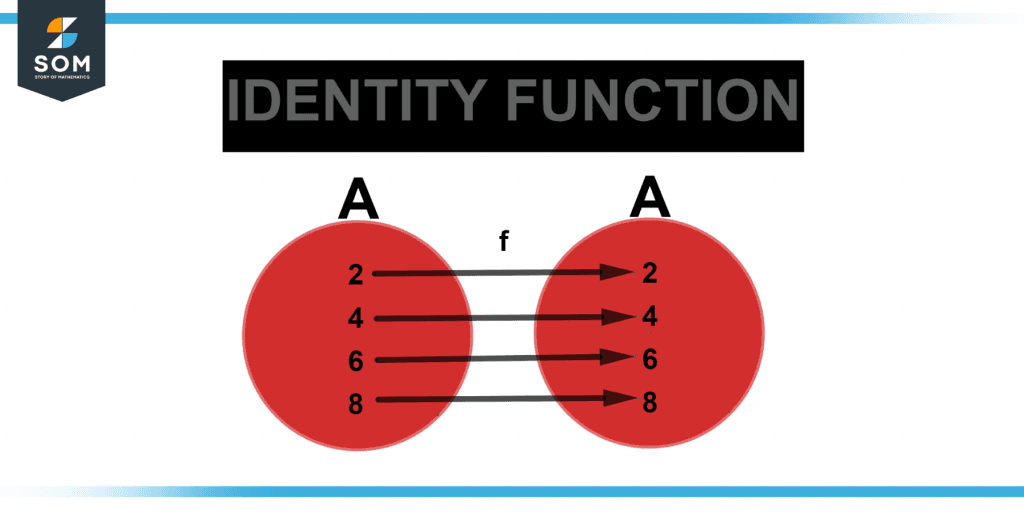
Figure 2 – Representation of identity functions.

Standard Identities

An equation with the formula x = Y is known as just an identity in maths if the conditions below are satisfied:

• There are several factors on both sides of the equality connection.
• The same outcome is produced by both sides when a particular constant is substituted for the variable.

An equality link may only be considered an identity if both conditions are satisfied. We don’t need to keep track of every relationship that a mathematician would refer to as an identity. Just a few widely used mathematical identities are essential in algebra, which might make the calculations easier.

Domain, Range, and Inverse of Identity Function

A real-valued function called an identity function may be written as a: B B such that y(x) = x, where x R. The scope of the expression g, in this case, is a collection of real numbers or R. The scope of identity functions and the domain are both the same. If the supply is 2, the output will also be 2, and vice versa if the supply is 0.

• The system functionality y(x) has R as its domain.
• The identity function’s y(x) range is also R.
• An identity function’s co-domain and range are equal sets—Onward with the identity function.

Identity Function Graph

We may display the values of the coordinates of x on the x-axis as well as the values of the coordinates of y on the y-axis to represent the graph of the equality function. An identity function has a graph that is a flat line through the origin. The domain and range for just an identity function are the same.

Figure 3 below shows the Identity Graph.

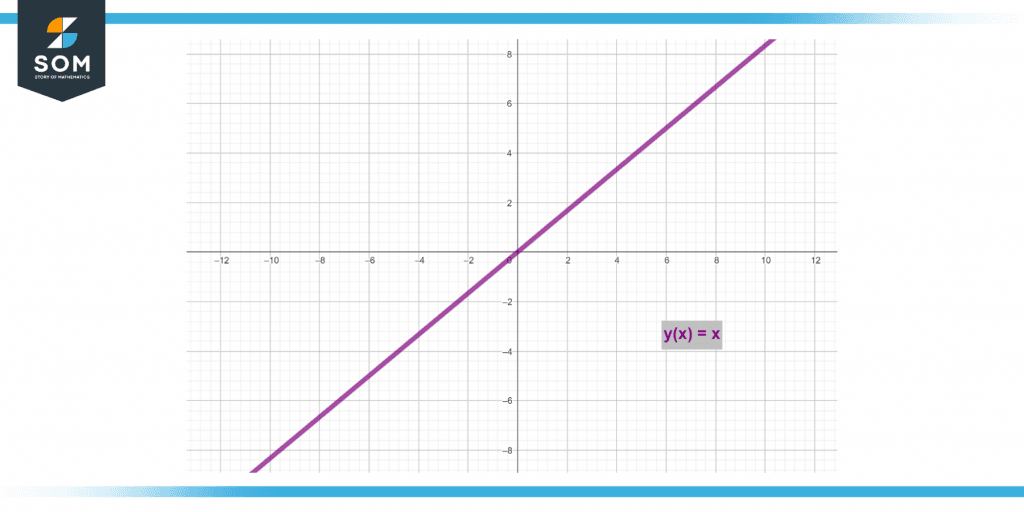
Figure 3 – Representation of identity graphs.

The graph above demonstrates that the linear model forms a 45° angle on both the x-axis as well as the y-axis. The identity function graph’s slope always remains at 1.

Common Identities

Algebraic Identities

Algebra is built on a few identities, including x+0=a and x+(-x)=0, while other identities $(a+b)^{2}=a^{2}+b^{2}+2ab$ and $a^{2}-b^{2}=(a+b)(a-b)$ are essential for extending and simplifying algebraic formulas.

Trigonometric Identities

Trigonometric equations include the specific function of one or more angles geometrically. They differ from triangle characteristics, which are identities that involve both a triangle’s angles and side lengths. In this article, only the latter are covered.

These identities are used when trigonometric function-based expressions need to be made simpler. Using the substitution method with a function first, then simplifying the resultant integral with such a trigonometric identity, is a typical strategy for integrating non-trigonometric functions, which is another effective use.

The equation $sin^{2}\theta + cos^{2}\theta = 1$ that holds for all true values of theta θ is one of the most well-known instances of a trigonometric identity. Alternatively, the formula cosθ = 1

Exponential Identities

If the base is not zero, the following identities apply to all integer exponents:

\[b^{m+n}=b^{m}+b^{n}\]

Exponentiation is not commutative, in contrast to addition and multiplication, for example, $2^{3}$=8.

Properties of Identity Function

Identity functions are frequently used to return a function’s parameters’ exact values, unaltered. A zero function or an unfilled function should be distinct from an identity function. The following are some of an identity function’s key characteristics:

• A linear function with real values is the identity function.
• An identity function’s graph forms a 45° angle with the x- and y-axes.
• The function is the reverse of itself since it is bijective.
• An identity function’s graph and its reverse are identical.

Examples of Identity in Mathematical Problems

Here are some examples 

Example 1

Factorize $(\mathsf{x^{4}}$ – 1) using common algebraic identities.

Solution

($x^{4}$ – 1) has the identity form, with a = ${(x^{2})}^{2}$ and b = 1. As a result,

\[(x^{4} – 1) =x^{2}-1^{2}\]

\[(x^{2}+1)(x^{2}-1)\]

Using the same Identity, where a = x and b = 1, it is possible to factorize the factor ($x^{2}$ – 1) further. So,

\[(x^{4} – 1) = (x^{2}+1)(x+1)(x-1)\]

Example 2

Find  (3m + 2n) (3m – 2n)

Solution

We already know that:

(p + q)(p – q) = $p^{2}-q^{2}$

In light of this:

(3m + 2n)(3m – 2n)  =$ (3m)^{2}-(2n)^{2}$

The equation becomes:

(3m + 2n)(3m – 2n)  = $9m^{2}-4n^{2}$

So, the answer is:

(3m + 2n) (3m – 2n) = $9m^{2}-4n^{2}$

All images are made using GeoGebra.

Hypothesis Definition < Glossary Index > Image Definition