Improper Fraction|Definition & Meaning

What Is an Improper Fraction? 

A fraction is inappropriate or improper when the fraction’s numerator is either greater or equal to the fraction’s denominator. For instance, the fractions 5/2 and 8/5 are examples of incorrect fractions. The numerator and the denominator are the components that make up every fraction. In mathematics, two primary types of fractions are distinguished by the values of the numerator and the denominator. These are referred to respectively as proper fractions and improper fractions.

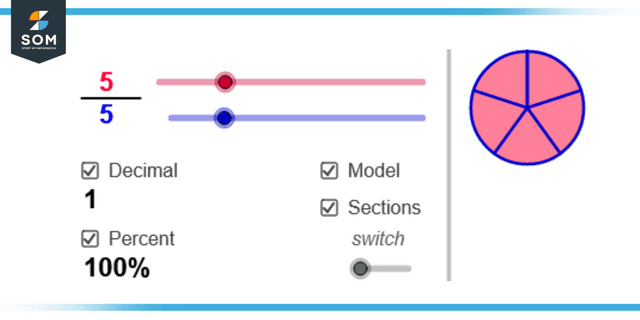
Figure 1: Representation of improper fraction.

History

Around 1600 BC, the Egyptians were the earliest known users of fractions, making the concept quite a bit older than that. There are many distinct kinds of fractions. A fraction is considered correct when the numerator is less than the denominator, as in the case of 1/2. Contrary to this, T, if the denominator is lower than the numerator or has the same size as the numerator, then the fraction is inappropriate. One such example is the score of 16/15.

One sort of fraction is known as an improper fraction, and it is characterized by having a numerator that is either equal to or greater than that of the denominator. Its value is either one or an integer more significant than one. Incorrect fractions are typically represented in mixed numerical form and simplified in some way since it is simpler to understand mixed fractions than improper fractions.

How To Simplify Improper Fractions?

We are now aware of what is meant by the term “improper fraction.” Let’s talk about how to simplify such fractions here

Step 1

First, determine whether or not the fraction given is correct.

Step 2

The second step is to interpret the denominator and determine the total number of parts that it divides the numerator into.

Step 3

Determine which factors are shared by both the numerator and the denominator.

Step 4

Remove the terms that are identical from both the numerator and the denominator.

Improper Fractions and Mixed Fractions

It is a fraction in which the fraction’s numerator is either larger than or equivalent to the value of the fraction’s denominator. For instance, 9/4 and 4/3 are both examples of incorrect fractions. In terms of numbers, they are consistently either equal to or bigger than 1. On the other hand, a fraction is said to be mixed when expressed as a composite of natural numerals and a proper fraction. This type of fraction is known as a mixed fraction. It is a more straightforward representation of an incorrect fraction. From a mathematical perspective, a mixed fraction will always be more significant than one. Moreover, if the rules are followed, any mixed fraction can be written as inappropriate.

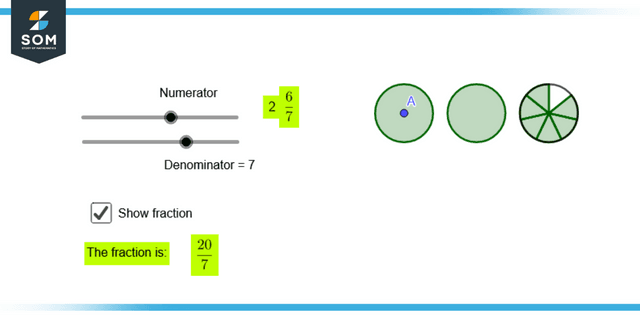
Figure 2: Representation of mixed numbers.

Reading and comparing mixed fractions to improper ones in everyday situations is typically more straightforward. This is because mixed fractions include both whole numbers and fractions. Following some fundamental methods, which you will become familiar with in the coming sections of this page, we can easily convert any improper fraction to a mixed number or any mixed fraction to an improper fraction.

Converting Improper Fractions to Mixed Numbers

Always remember that the denominator of the improper fraction’s mixed fraction form will be the same as the denominator of the underlying fraction. Because mixed numbers are believed to be a simplified form of improper fractions, it is essential to learn to convert between the two types of numbers. The following is a list of the procedures that need to be taken to transform an improper fraction into a mixed number:

Step 1

Firstly, divide the numerator by the denominator.

Step 2

In the second step, you will determine the values for the quotient and the remainder.

Step 3

To write a fraction in the form of a mixed number, arrange the values of the quotient, the remainder, and the divisor.

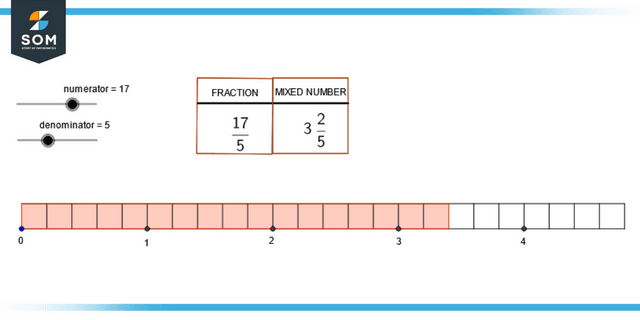
Figure 3: Converting improper fraction to mixed number.

How To Solve Improper Fractions?

The process of simplifying the value of an improper fraction after it has been solved by executing arithmetic operations on it is called “solving” improper fractions. The fundamental arithmetic operators in mathematics are addition, subtraction, multiplication, and division. These are the four arithmetic operations. The only difference between solving an improper fraction and calculating any other proper fraction is that, in this case, we need to simplify the result and represent it in mixed numbers. Otherwise, solving an improper fraction is similar to solving any other proper fraction.

Subtracting Improper Fractions

In a manner analogous to how we added the improper fractions, we can subtract them.

• The first thing to do is determine whether the denominators are the same.
• The second step is to make the denominators more reasonable.
• The final step is to remove the fractions that have been given and, if necessary, simplify them.

Examples of Improper Fractions

Example 1

Small fish are fed three times a day. The amount of fish that are fed is measured in terms of the total weight of the fish fed.

During the morning feeding, 3/2 of tons of fish are fed. During the afternoon, the number (or weight) of the fish fed will be 4/3 of a ton more than the ones in the morning feeding. If the total number of fish fed on a day is 27/5 of a ton, how much is fed during the feeding at night?

Solution

Let’s assume that the weight of fish fed at night = x tons

In the morning, the weight of fish fed = 3/2 tons

In afternoon the weight = 4/3 + 3/2 = 17/6. Solving for x:

3/2 + 17/6 + x = 27/5

13/3 + x = 27/5

x = 27/5 – 13/3

x = (81-65)/ 15

x = 16/15

So, during the night feeding, 16/15 of tons of fish is fed.

Example 2

Jame’s father is 7 1/2 feet tall. Jame is 5 feet tall. How many times taller is Jame’s father than him?

Solution

Jame’s father height = 7 1/2 feet

Jame’s height = 5 feet

= (15/2)/ 5/1

= 15/2 * 1/5

= 15/10

= 3/2

So, Jame’s father is 3/2 times taller than him.

All images/graphs are created using GeoGebra.

Imperial System Definition < Glossary Index > Included Angle Definition