JUMP TO TOPIC
Included Angle|Definition & Meaning
Definition
The angle created at the vertices of two neighboring triangle legs is an included angle. If two legs meet at a vertex, they are considered adjacent. This angle’s measurement can be utilized to determine the triangle’s other characteristics and values.
An included angle is a type of angle that can be produced in geometry by using 2 lines that meet at the same location.
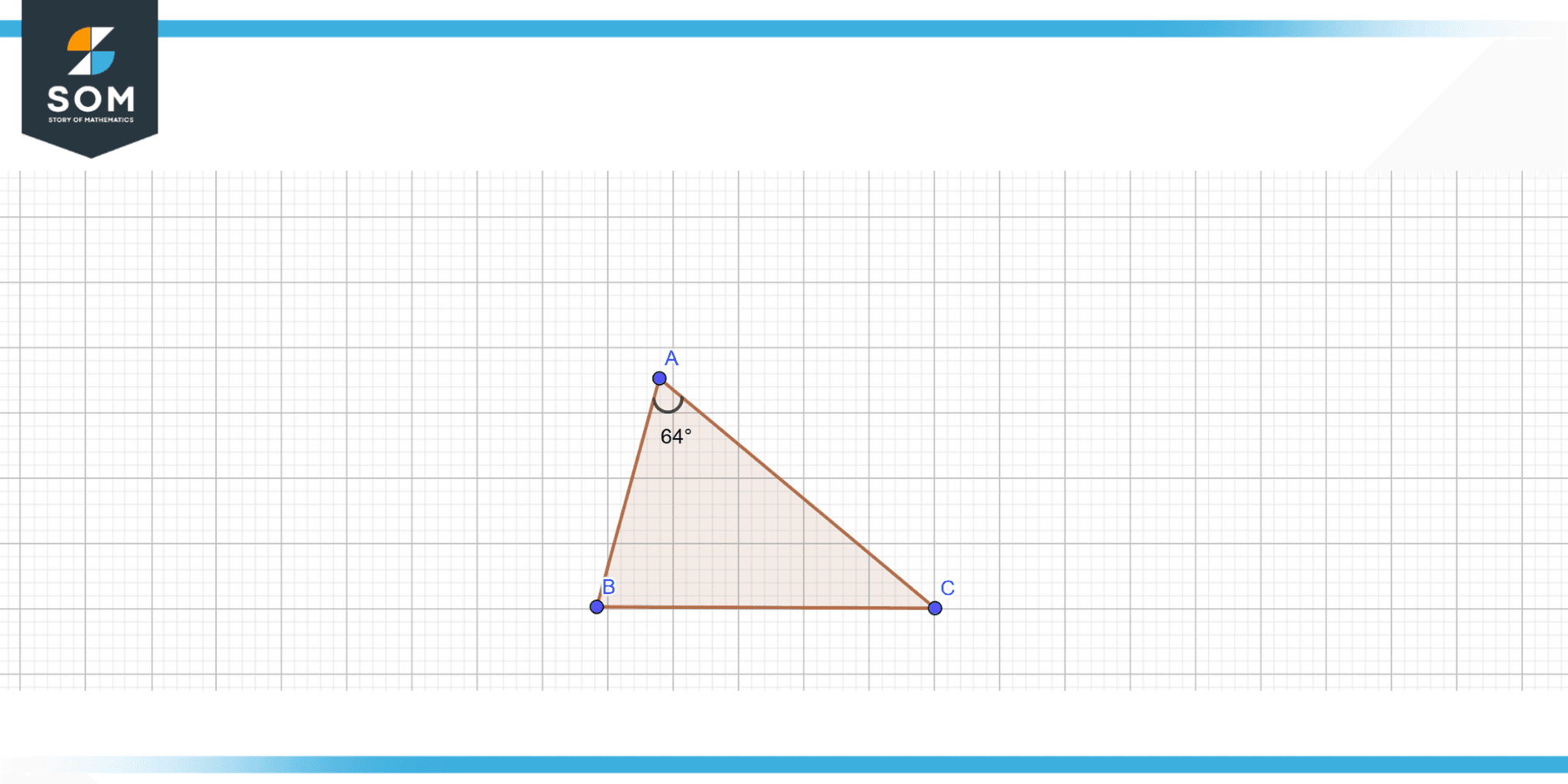
Figure 1 – The included angle of a triangle
The endpoint that is shared is referred to as the vertex, as well as the two lines that make up the angle are referred to as the sides of that same angle. Calculated in degrees as well as radians, with 360 degrees as well as 2 radians corresponding to a full circle, an angle can be expressed using either system.
The included angle is frequently used to define the angle formed by two planes within three-dimensional space or by two lines in a plane. In addition to that, you can use it to talk about the angle that exists only between sides of just a polygon or even the angle that exists among the faces of such a polyhedron.
In geometry, one of the most significant concepts is called the included angle, and its purpose is to define the shape and size of different figures and objects. In addition to this, it is utilized in a variety of scientific and engineering applications, as well as in the field of trigonometry and other sub fields of mathematics.
What Is Included Angle and Included Side?
A common leg between 2 angles is known as an included side. In contrast to the included angle, this will be expressed as a length in units of measure like inches or centimeters.
The included side joins two angles, whereas the included angle includes two neighboring legs. The opposite component is on either side of the included angles and legs, which are in the midst of the three measurements.
Examples of Included Angles
An angle that isn’t included in the definition of the leg is called a non-included angle. This means that any one of the legs that are next to each other does not possess a value. Both of the legs that are next to one another need to have a value specified for the angle to be regarded as an included angle.
In order for the angle to be considered part of the triangle, it must be located between the two sides of the triangle. If the angle is just adjacent to one leg, then it is omitted from consideration.
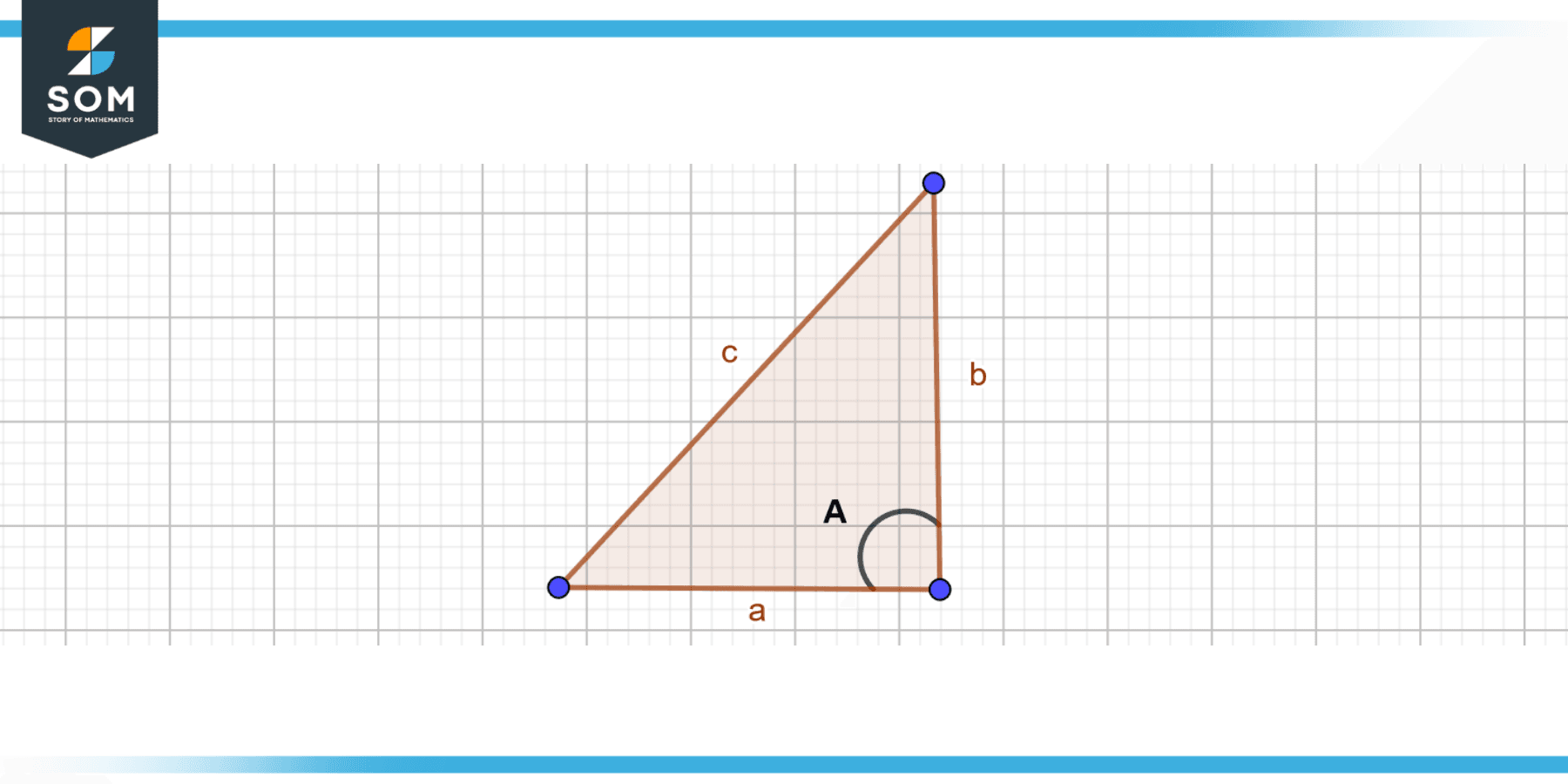
Figure 2 – Right angle triangle showing the included angle
The following two lines showing the included angle.
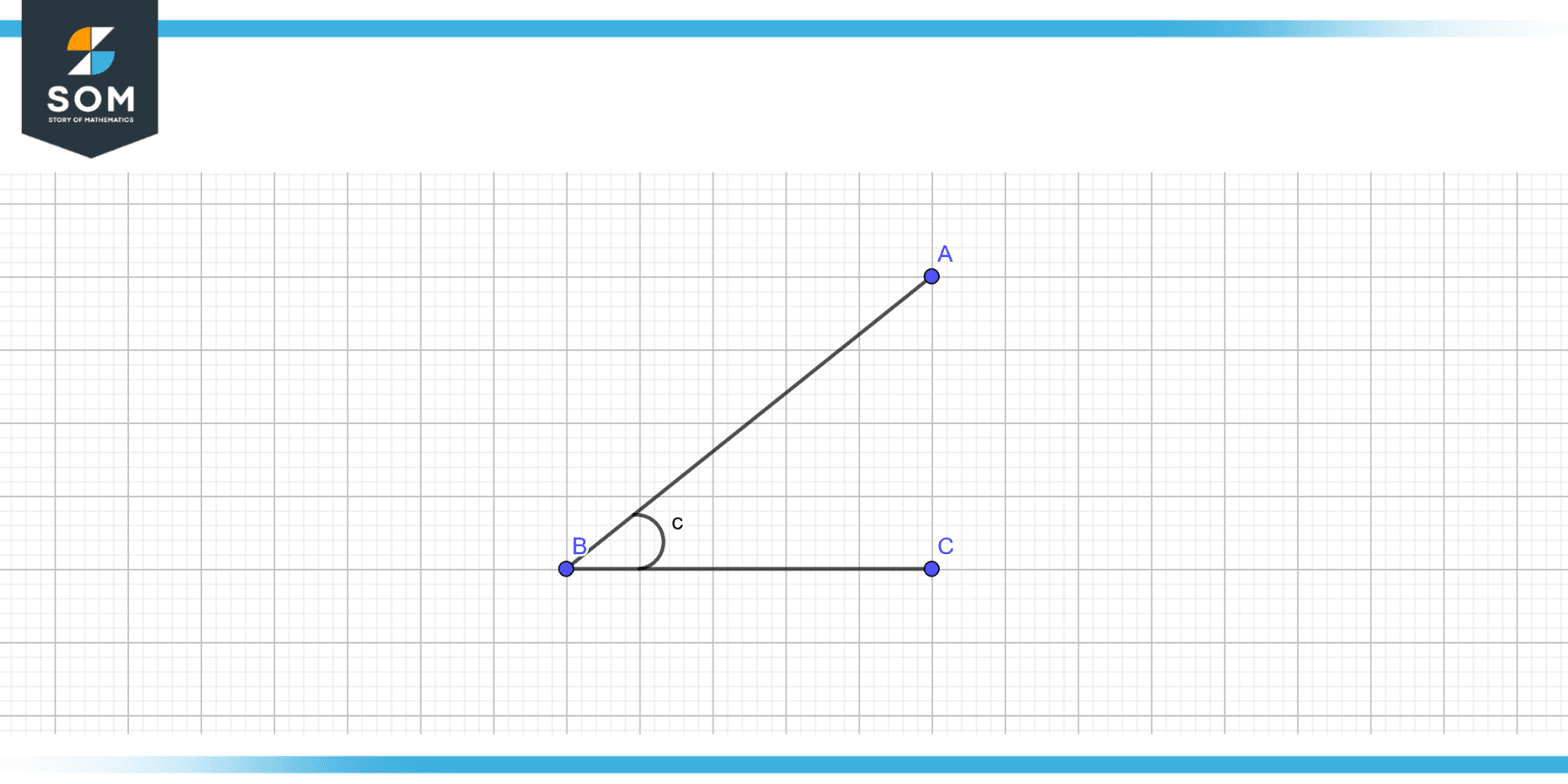
Figure 3 – Two lines showing the included angle
Uses of the Included Angle
Included angles are used in several applications.
Before going through them, know that just like the angle formed by two lines or planes that meet constitutes the included angle, the angle formed by the intersection of 2 faces of a solid object is also the same thing. It can also be known as the inner angle or even the “angle between.” Both of these names refer to the same thing.
- When defining the angle that exists between two lines in geometry that meet at a point, an included angle is frequently the method of choice.
- When determining the length of either side of such a triangle in trigonometry, an included angle is one of the three angles that must be considered together with the length of the remaining 2 sides & the included angle.
- When it comes to engineering and building design, the included angle is one of the most important factors considered when evaluating the robustness and steadiness of structures like bridges, buildings, and machinery. For instance, the load-carrying capability of a truss construction is affected by the angle that is included between two of the beams that make up the structure.
A Numerical Example of the Included Angle
Example 1
Determine the range of values that can be assigned to an included angle of a triangle whose side lengths are 5 centimeters and 8 centimeters and whose area is 15 centimeters square.
Solution
Given that:
The side length of the triangle is = 5 cm
The side length of the triangle is = 8 cm
The area of a triangle is = 15 cm2
We have to find the included angle.
So, if the required included angle is θ, then:
0.5 x 5 x 8 x sin(θ) = 15
By simplifying, we get:
sin(θ) = 15 / 20
By calculating the sin inverse, we get:
= 48.6 degrees
The included angle for the given values is 48.6 degrees.
Example 2
Determine the range of values that can be assigned to an included angle of a triangle whose side lengths are 5 centimeters and 10 centimeters and whose area is 15 centimeters square.
Solution
Given that:
The side length of the triangle is = 5 cm
The side length of the triangle is = 10 cm
The area of a triangle is = 15 cm2
We have to find the included angle.
So, if the required included angle is θ, then:
0.5 x 5 x 10 x sin(θ) = 15
By simplifying, we get:
sin(θ) = 15 / 25
By calculating the sin inverse, we get:
= 36.86 degree
The included angle for the given values is 36.86 degrees.
Example 3
Determine the range of values that can be assigned to an included angle of a triangle whose side lengths are 5 centimeters and 20 centimeters and whose area is 15 centimeters square.
Solution
Given that :
The side length of the triangle is = 5 cm
The side length of the triangle is = 20 cm
The area of a triangle is = 15 cm2
We have to find the included angle.
So, if the required included angle is θ, then:
0.5 x 5 x 20 x sin(θ) = 15
By simplifying, we get:
sin(θ) = 15 / 50
By calculating the sin inverse, we get:
= 17.45 degree
The included angle for the given values is 17.45 degrees.
All mathematical drawings and images were created with GeoGebra.
