JUMP TO TOPIC
Included Side|Definition & Meaning
Definition
Included sides are the sides linking two angles in triangles and other polygons. The angle between two lines is regarded as ‘included’ between two lines. The included side is also referred to as the leg that connects two angles. Triangles or polygons are made up of these sides that connect two angles and are shared by both angles.
Finding Properties of Triangle From Included Sides
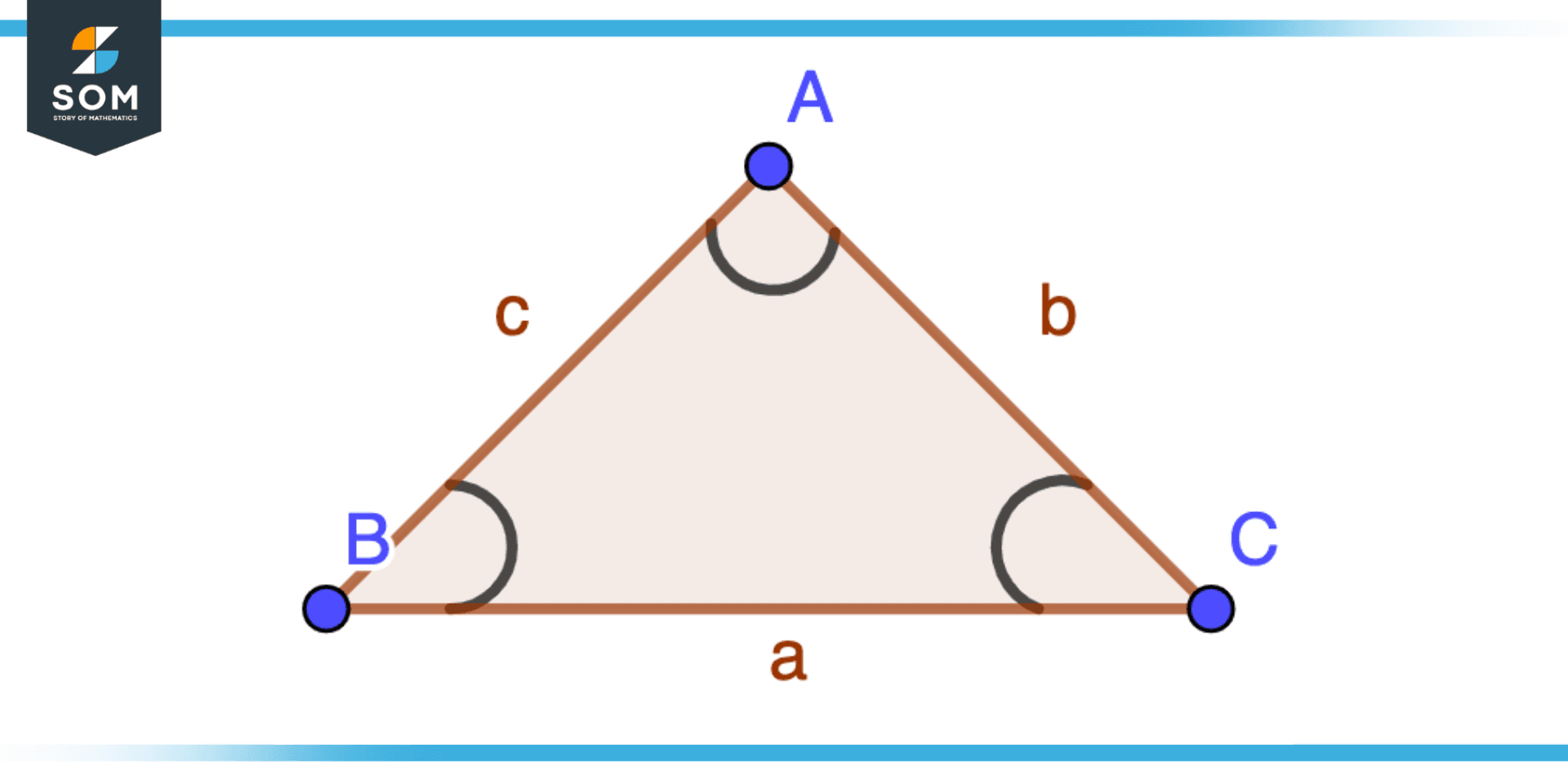
Figure 1 – Included Side of a Triangle ABC
Because they can be used to establish various aspects of triangles, included sides are significant in geometry. These characteristics include the triangle’s area, perimeter, and angles.
Area of Triangle
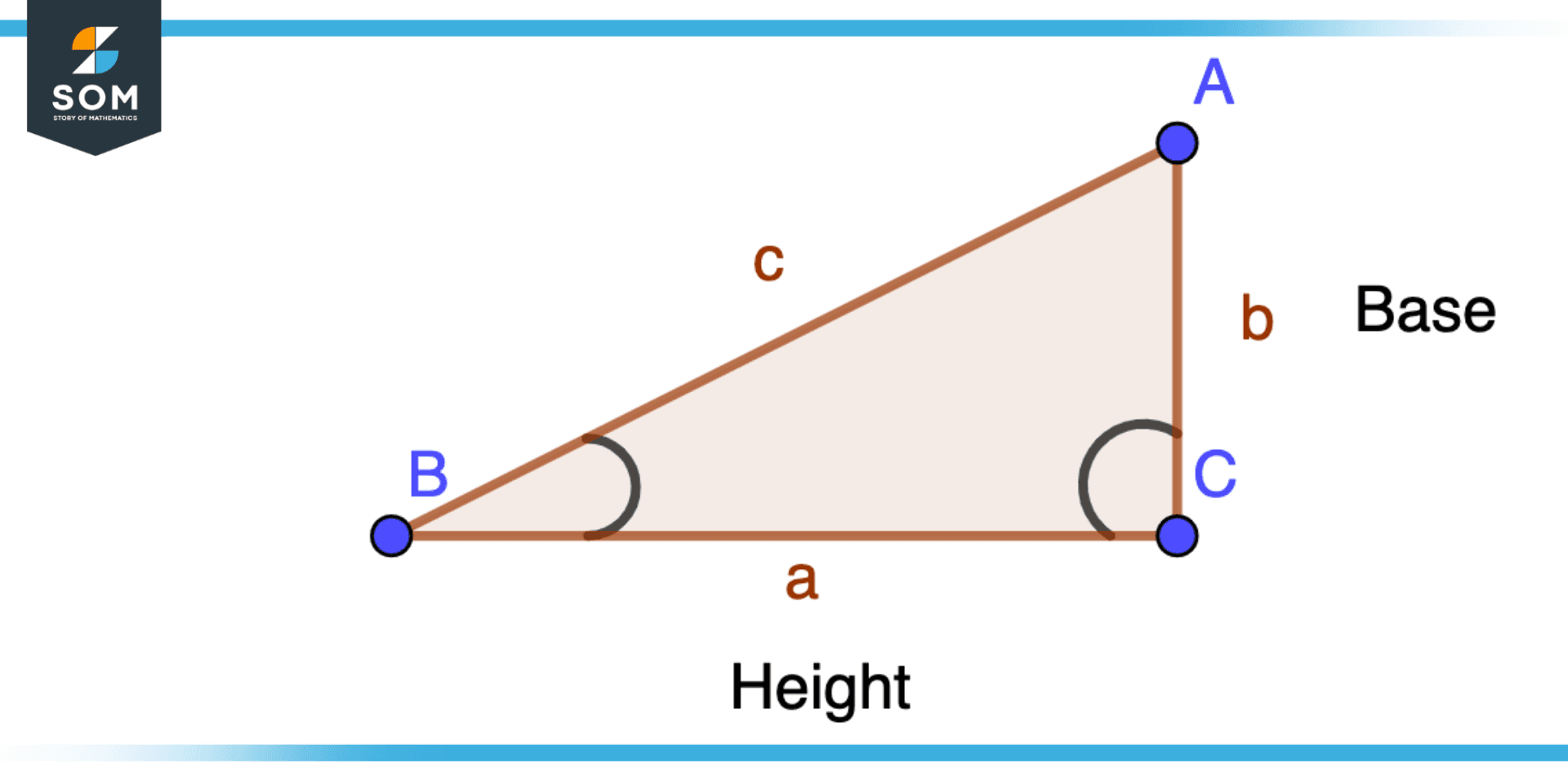
Figure 2 – Area of Triangle from included side
Utilizing ratios is one way that included sides can be used to ascertain a triangle’s characteristics. For instance, the area of a triangle can be calculated using the ratio of the lengths of its included sides. A triangle’s area is determined by multiplying its base by its height and dividing that result by two. This is known as the area formula for triangles.
Perimeter of Triangle
The perimeter of a triangle can also be calculated using the triangle’s included sides. The perimeter of a triangle equals the sum of the lengths of its three sides. The lengths of all three sides are simply added to determine a triangle’s perimeter.
Angles of Triangle
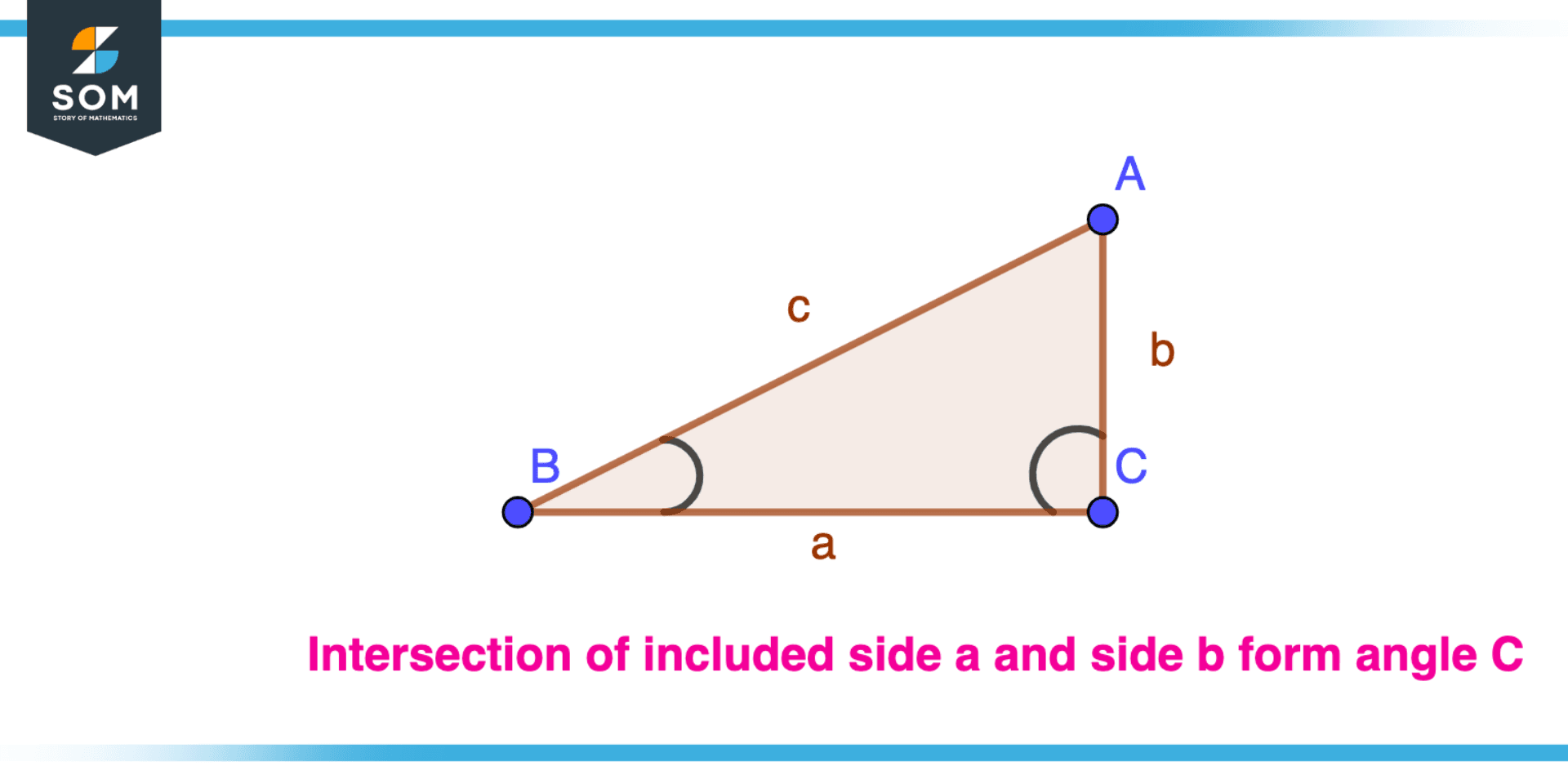
Figure 3 – Finding Angle of triangle from included side
A triangle’s included sides can be utilized to calculate its angles in addition to these other attributes. The intersection of two sides creates each angle in a triangle, and the length of the included side determines the angle’s measurement. The angle will be greater the longer the included side is.
Law of Cosines
The Law of Cosines is another theorem that deals with included sides and is used to calculate a side’s length in a triangle when the other two sides lengths and the size of the included angle are known. According to the Law of Cosines, one of the sides of the triangle square is equal to the addition of squares of the rest of the two sides, less by twice the product of the sides other two lengths and the cosine of the included angle.
Law of Sines
There are other geometric formulas that incorporate sides and angles. One of these formulas, known as the Law of Sines, is used to determine a triangle’s angle’s measure when both its included angle and side lengths are known. The law of Sines states that the ratio of a triangle’s length to the sine of the included angle is equal to the ratio of its length to the sine of the other side.
Included Side Vs. Included Angles
Included Side
A side that is encompassed between two other triangle sides is said to be an included side. It is a side of the triangle that is not the base. A triangle has three included sides, and they are significant in geometry because they may be used to calculate the triangle’s area, perimeter, and angles, among other things.
Included Angle
On the other hand, an included angle is an angle that is formed by the intersection of two sides of a triangle. It is an angle that is enclosed between the two sides of the triangle. In a triangle, there are three included angles, and these angles are significant in geometry because they can be used to calculate the triangle’s area, perimeter, and angles, among other things.
Differences
One of the main differences between included sides and included angles is that included sides are lengths, while included angles are measures of rotation. Included sides are measured in units of length, such as inches or centimeters, while included angles are measured in units of angle, such as degrees or radians. The included side is used to solve problems involving triangles and other geometric shapes, while the included angle is used to describe the angles and relationships between sides of a shape.
“Angle Side Angle” Theorem
The angle-side-angle (ASA) theorem states that two triangles are congruent if two angles and one of their included sides are congruent (equal) to two angles and the other triangle’s included side. This suggests that the two triangles are identical in terms of size and shape.
The theorem states that two triangles are congruent in relation to the included side if the lengths of their included sides are equal. For instance, if the included side of one triangle is the same length as the included side of another triangle and vice versa.
For example, consider two triangles ABC and DEF. If the measure of angle A is equal to the measure of angle D, the measure of angle C is equal to the measure of angle F, and the length of side BC is equal to the length of side EF, then triangles ABC and DEF are congruent.
Summary
In summary, a side that lies between the two angles created by the other two sides of a triangle is referred to as an included side in geometry. The triangle’s median is another name for the included side, the length of the included side of a triangle can be used to define specific trigonometric functions these functions are employed to address issues involving triangles and circles and are defined in terms of the ratios of a triangle’s sides. As well as provide important information about the triangle and its properties. The included side of a triangle also plays a significant role in the study of geometry and trigonometry.
Solved Examples of Included Sides
Example 1
Consider a triangle with sides of lengths 5, 12, and 13. This triangle is a right triangle because the side lengths satisfy the Pythagorean theorem (the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides). Let’s call this triangle ABC. Side AB has a length of 5 and is opposite angle BAC. Side AC has a length of 12 and is opposite angle CAB. Side BC has a length of 13 and is the hypotenuse, which is opposite the right angle. Find the included side.
Solution
In this example, side BC is the included side. It is bounded by angles BAC and CAB and is opposite the right angle. The length of the included side (side BC) can be used to calculate the measure of the included angles using trigonometric functions.
Example 2
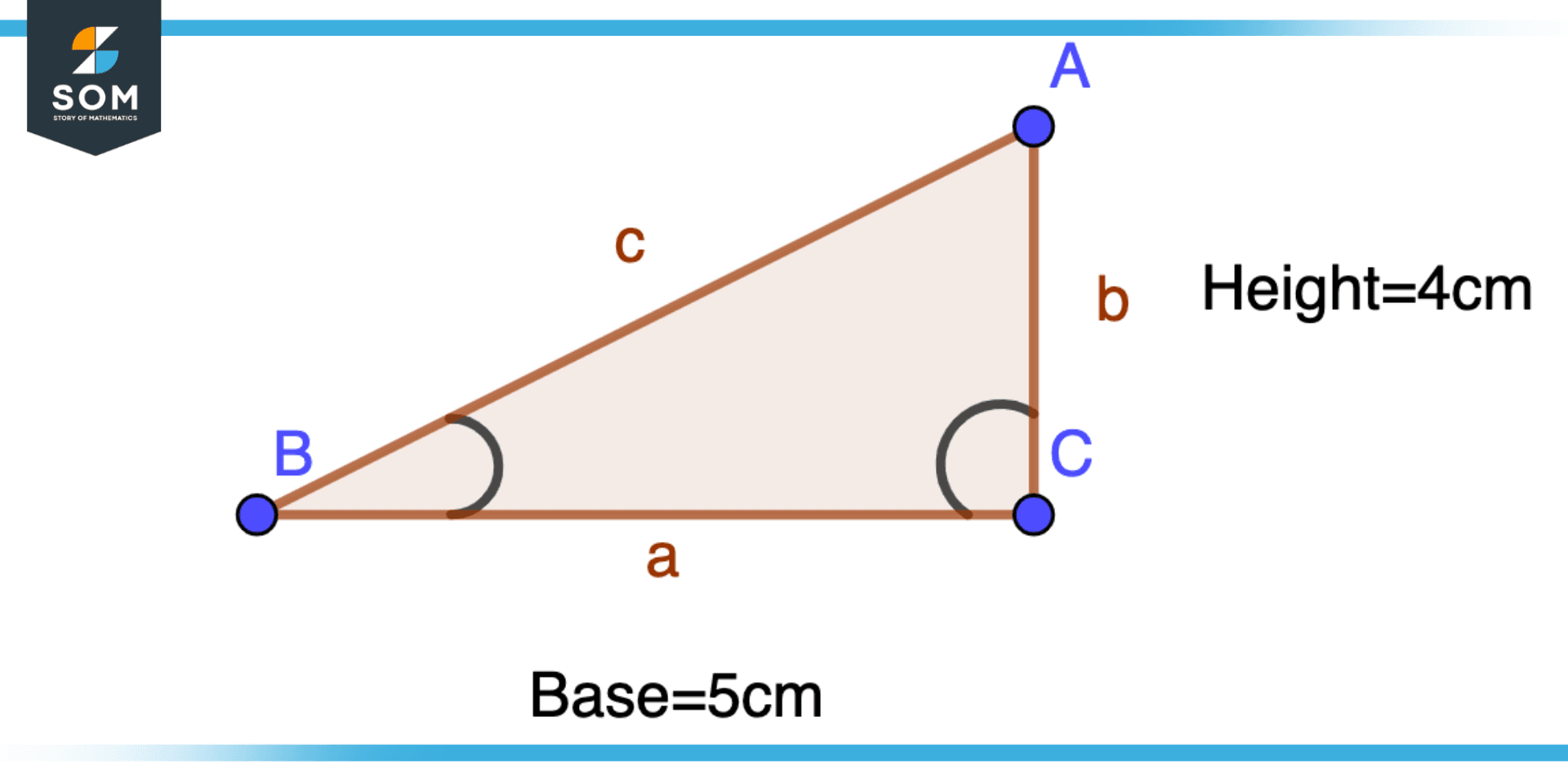
Figure 4 – Example of finding Area of triangle from included side
Consider a triangle ABC having three included sides a,b, and c. Find the area of a triangle using the concept of finding the area of a triangle using included sides.
Solution
Area of triangle = $\dfrac{1}{2}$ x Base x Height
Area of triangle = $\dfrac{1}{2}$ x 5 x 4
Area of triangle = $\dfrac{1}{2}$ x 20
Area of triangle = 10
All mathematical drawings and images were created with GeoGebra.
