JUMP TO TOPIC
Increase|Definition & Meaning
Definition
The literal opposite of decrease, to increase means to make larger or greater, e.g., stretching out a rubber band increases its size, and filling a cup with a drink increases the volume of the fluid contained in it. It is closely related to the term increment, and one can think of it as an addition, though it is not always used in that sense.
An increase refers to a change in a quantity or value, typically from a lower value to a higher one. It is used to describe the growth or enhancement of something over time, such as a rise in a financial market, an increase in population, or a growth in demand for a product. For example:
Start Value: \$500
End Value: \$1000
Increase: \$1000 – \$500 = \$500
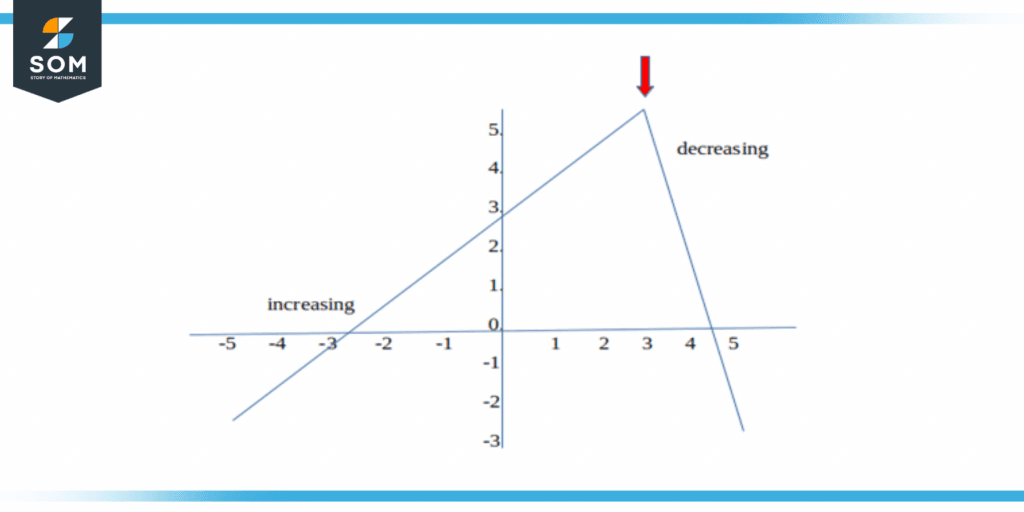
Figure 1 – Increasing and decreasing function
In summary, increasing values go up as the input increases, while decreasing values go down as the input increases.
In mathematics, an increase is often represented as a positive change in quantity. The concept of increase is also used in various other fields, including economics, sociology, and psychology. In these fields, an increase refers to an improvement or growth in a particular aspect, such as an increase in a country’s standard of living, a rise in education levels, or a growth in self-esteem.
Overall, the concept of increase is a key part of many different fields and is used to describe changes and improvements in various aspects of life.
Detailed Explanation
An increase refers to a change in a quantity or value where the new value is greater than the original value. It is often used to describe the growth or enhancement of a quantity over time and can be represented by a positive change in an amount.
The concept of increase is used in a variety of mathematical fields, including algebra, calculus, and statistics. In algebra, for example, the concept of increase is used to solve equations and simplify expressions. In calculus, the concept of increase is used to analyze the rate of change in a function, and in statistics, it is used to analyze data and make predictions about future trends.
Moreover, to represent a positive change in a quantity, the concept of increase is also used to describe the rate at which a quantity is changing. For example, if a quantity is increasing at a rate of 2 units per second, this means that the value of the quantity changes by 2 units every second.
Overall, the concept of increase is an important part of mathematics and is used to describe the growth and enhancement of quantities over time, as well as the rate at which quantities change.
Increasing Symbol
The symbol for an increasing function is “>,” which means “greater than.” For example, if f(x) > g(x) for all values of x in a given interval, it means that the value of the function f(x) is always greater than the value of the function g(x) in that interval.
The symbols “>” and “<” are used to compare the values of two functions and indicate the relative size of their outputs. The symbols help to visually represent the direction of change in a function and make it easier to understand the relationship between different functions.
Increasing and Decreasing Functions
In mathematics, increasing and decreasing functions are types of functions that describe how a dependent variable changes in relation to an independent variable.
Increasing Functions
An increasing function is a function where, as the value of the independent variable increases, the value of the dependent variable also increases. For example, if a function represents the height of a plant as it grows, the height of the plant will increase as the time (the independent variable) increases.
Decreasing Functions
A decreasing function, on the other hand, is a function where, as the value of the independent variable increases, the value of the dependent variable decreases. For example, if a function represents the distance between two moving objects, the distance between the objects will decrease as the time (the independent variable) increases.
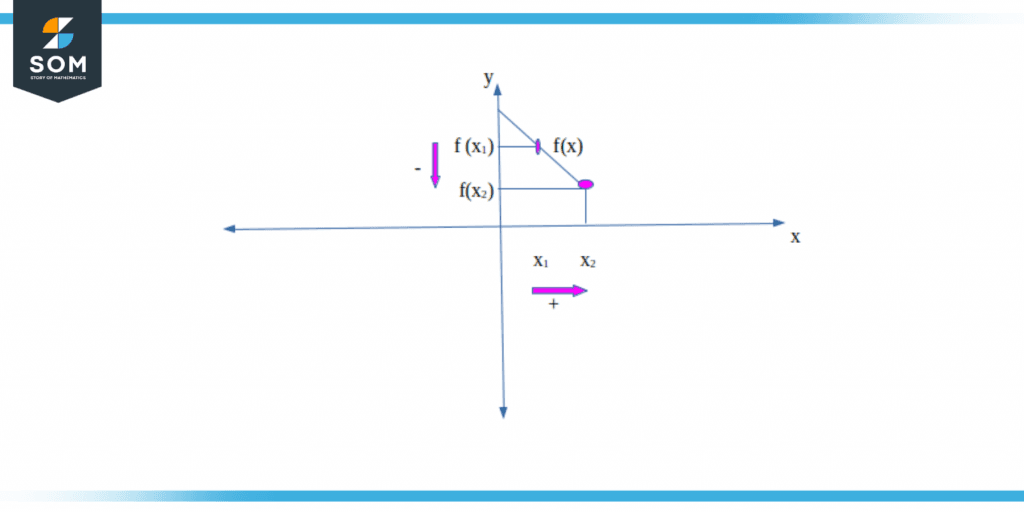
Figure 2 – Increasing Decreasing function
Increasing and decreasing functions can be determined by analyzing the sign of the derivative of the function. If the derivative is positive over a certain interval, then the function is increasing over that interval, and if the derivative is negative over a certain interval, then the function is decreasing over that interval.
Increasing and decreasing functions are important in mathematics, particularly in calculus, where they are used to analyze the rate of change and the maximum and minimum values of a function. These functions play a role in many real-world applications, including economics, engineering, and physics.
A function is considered increasing if as the input (x) increases, the output (y) also increases. Conversely, a function is considered decreasing if, as x increases, y decreases. These concepts are important in calculus, where increasing and decreasing functions play a crucial role in optimization problems.
A key tool in analyzing increasing/decreasing functions is the first derivative test, which involves computing the derivative of a function and analyzing its sign to determine if the function is increasing or decreasing over a given interval.
Difference Between Increasing and Decreasing Values
The terms “increasing value” and “decreasing value” are used to describe the direction of change in a function or a mathematical expression.
An increasing value refers to a situation where a quantity increases as the input (x) increases. For example, if a function y = f(x) is increasing, then for any two points x1 and x2 such that x1 < x2, the corresponding outputs f(x1) and f(x2) will satisfy f(x1) < f(x2). This means that as the input x increases, the output y also increases.
A decreasing value refers to a situation where a quantity decreases as the input (x) increases. For example, if a function y = f(x) is decreasing, then for any two points x1 and x2 such that x1 < x2, the corresponding outputs f(x1) and f(x2) will satisfy f(x1) > f(x2). This means that as the input x increases, the output y decreases.
Increase Percentage
To increase a percentage, simply multiply the original percentage by a value greater than 1.

Figure 3 – Percentage Increase
The amount of increase can be represented as a decimal or a percentage, depending on the desired result.
A Few Examples of Value Increases
Example 1 – Increase by Percentage
Increase 60% by 20%.
Solution
Multiply 60% by 1.2 (1 + 20% = 1.2) to get 72%.
Example 2 – Decrease by Percentage
A decreasing percentage refers to a situation where a quantity decreases by a certain percentage over time. If a product’s price decreases by 10%, it means that its price has gone down by 10% of its original value.
Solution
This can also be expressed as a fraction, where the decrease is represented by 1 – (percent decrease as a decimal). A decreasing percentage can be used to describe various types of changes, such as declining stock prices, decreasing interest rates, or declining sales.
All the figures above were creating using GeoGebra.
