Independent Event|Definition & Meaning

 It is one of several kinds of occurrences in probability. Let us now look at the description of independent events, including a Venn diagram, examples, and how they vary from mutually incompatible events. 

Figure 1 below shows the Probability of Independent Events.

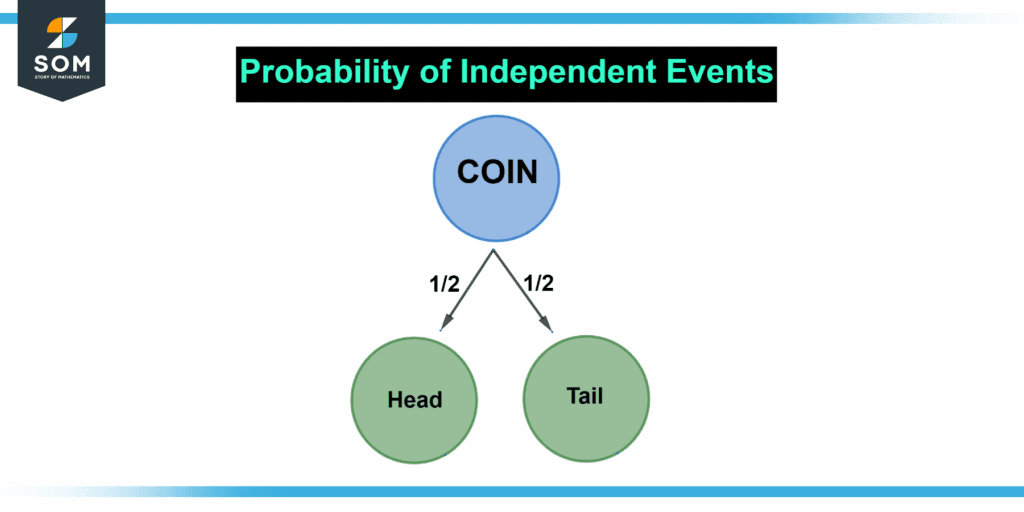
Figure 1 – Representation of an independence event.

What Exactly Is an Independent Event?

The two occurrences are independent if the outcome of one has no impact on the outcome of the other. On the other hand, an independent event is a situation in which each occurrence does not affect the chance of another.

In probability, independent occurrences correlate to real-world events. Consider how excellent scores on an exam have little influence on what your neighbors are up to.

Similarly, taking a taxi to the market has nothing to do with your capacity to find your favorite movie on YouTube. Another way to put it is that an independent occurrence is not dependent on another event first occurring.

The collection of inquiry outcomes is known as occurrences in probability. Events include independent occurrences, dependent happenings, conditionally exclusive happenings, and so on.

If the likelihood of an event A happening is not influenced by the occurrence of another event B. A and B are termed independent occurrences.

Figure 2 below shows if A and B are independent events.

Figure 2 – Formula for an independent event.

Venn Diagram of Independent Events

Let us use a Venn diagram to demonstrate the requirement of independent events.

Polynomial: Assuming X and Y represent independent occurrences, then X and Y’ must also be. Because occurrences A and B constitute independent.

Figure 3 below shows the Venn diagram of independent events.

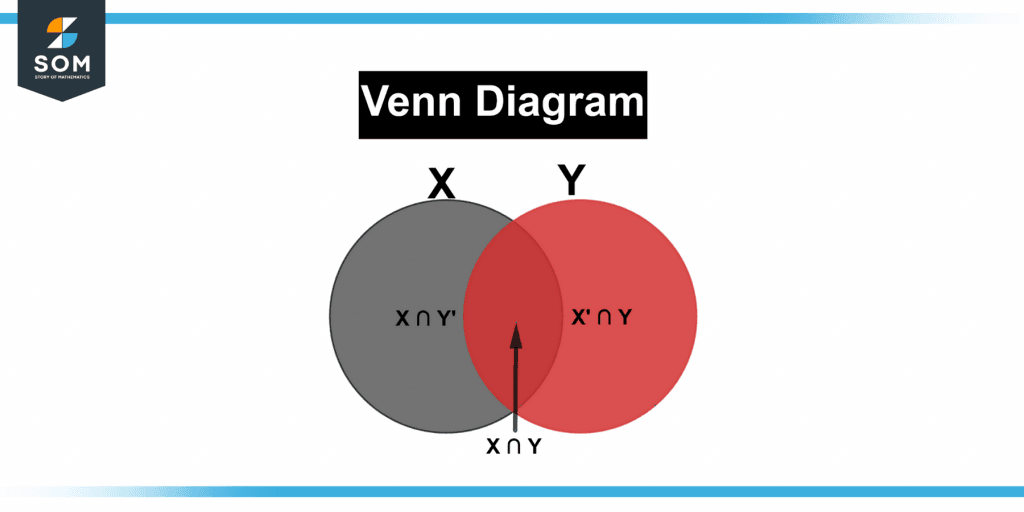
Figure 3 – Representation of independent event using a Venn diagram.

Calculating the Probability for the Independent Events

We take the following example to calculate the probability of an independent event.

Andrew is paying careful attention to a juggler at the circus. He has many colored juggling clubs: red, two green, and three blue. He makes an error all of a sudden. A member of the juggling club is discarded and re-selected. The second juggling club has now fallen from his grasp. What is the likelihood that the first juggling club will be blue and the second tossing club will be green?

It can be challenging to respond. Andrew’s choice of clubs is unrelated to any past incidences, and hence the clubs might have any of the colors. Such occurrences are independent events since they are unaffected by preceding events.

Probability: Probability is associated with potential. It is a numerical science that investigates the probability of a rare occurrence. The value can range from 0 to 1. Probability has been established in mathematics to forecast the possibility of events occurring. A probability is a degree to which such is likely to occur. 

This is the fundamental probability philosophy, which is also utilized in probability distribution and educates you about the likely results of a random experiment. To determine the likelihood of a specific event, we still must calculate the overall number of possible possibilities.

The conditional formula, which is presented below, must be used to calculate the probabilities for independent events: The conditional probability of event B inside the absence of event A is P(A/B) if the probability of occurrences A and B seem to be P(A) and P(B), respectively. The conditional formula is shown below.

\[\mathsf{P\left(\frac{A}{B}\right)=\frac{P(A\cap B)}{P(B)}}\]

Method for Recognizing Independent Events

Before using probability formulae, one must first recognize an independent event. Here are some procedures to take to determine if the probability relates to a dependent and independent event:

• Step 1: Determine whether the events may occur in any sequence. If yes, proceed to Step 2; otherwise, proceed to Step 3.
• Step 2: Determine whether one occurrence influences the result of the other. If yes, proceed to Step 4; otherwise, proceed to Step 3.
• Step 3: The incident is self-contained. Use the equation of independent events to get the solution.
• Step 4: The occurrence is conditional. Use the dependent event formula to find the solution.

Examples of Independent Events

Here are some examples of independent events

Example 1

Joseph & David are gaming with cards, and there are 52 game cards in a deck. Joseph drew a replacement card at random. Then he told David about the chances of drawing a queen, followed by a king.

Solution

As we can see, this probability has an independent occurrence condition:

P (drawing a queen in a first condition) = $\mathsf{\dfrac{4}{52}}$ 

P (drawing the king within the second condition following a queen with replacements) = $\mathsf{\dfrac{4}{52} \times \dfrac{4}{52}}$

$\mathsf{\dfrac{16}{2704}}$ = $\mathsf{\dfrac{1}{169}}$ 

P (drawing the queen followed by the king) = $\mathsf{\dfrac{4}{52}}$

P = $\mathsf{\dfrac{1}{169}}$  (drawing the queen followed by the king).

Example 2

A juggler uses seven red, five green, and four blue balls. After his stunt, he loses a ball and picks it up by mistake. Another ball falls as he continues. What is the likelihood that the initial ball dropped is blue and the second ball was green?

Solution

Because the juggler selects the first ball, the sampling unit for both balls is 16 because both events are independent.

P (blue ball) = $\mathsf{\dfrac{4}{16}}$ is the chance that the initial ball is blue.

P(green ball) = $\mathsf{\dfrac{4}{16}}$ is the chance that the second ball is green.

The likelihood that the initial ball is blue, as well as the second ball, was green is as follows:

P(blue and green) = P(blue) P(green) = $\mathsf{\dfrac{4}{16}}$ = $\mathsf{\dfrac{1}{16}}$

Example 3

According to a poll, six out of ten individuals consume pizza. What is the likelihood that all three persons will eat pizza if three people are picked randomly with replacement?

Solution

If three persons are picked at random with such a replacement that eats pizza, the likelihood that all three persons eat pizza is:

P(person 1 likes pizza) = $\mathsf{\dfrac{9}{10}}$ 

P(person 2 likes pizza) = $\mathsf{\dfrac{9}{10}}$  

P(person 3 likes pizza) = $\mathsf{\dfrac{9}{10}}$  

P(person 1, 2, and 3 love pizza) = $\displaystyle\mathsf{\frac{9}{10} \times \frac{9}{10} \times \frac{9}{10} = \frac{729}{1000}}$

All Images are made using GeoGebra.

Increment Definition < Glossary Index > Indeterminate Definition