JUMP TO TOPIC
Indeterminate|Definition & Meaning
Definition
The word “indeterminate” represents an anonymous value. The indeterminate state is a Mathematical term that points out that we are not able to decide the actual value even after substituting the limits.
An indeterminate is an additional expression for a variable. An indeterminate equation has greater than one solution. For instance x + y = 2, Without additional data we are unable to say exactly what x and y actually are. So we can say that An indeterminate expression cannot be exactly determined.

Figure 1 – Indeterminate solutions are not completely solvable
Both of the functions approach zero in the limit, mainly when the indeterminate state appears while assuming the ratio of two functional operations. Such forms are called “indeterminate form 0/0”. Again, the indeterminate form can be acquired in addition, multiplication, subtraction, and also exponential operations.
Indeterminate Forms of Limits
If a mathematical form is not definitively or exactly determined, it can also be expressed to be indeterminate. Various forms of limits are communicated to be indeterminate when simply understanding the limiting conduct of particular aspects of the expression is not adequate to really decide the all-around limit.
For instance, a limit of the form 0/0, i.e., $lim_{x \rightarrow 0} f(x)/g(x)$ where $lim_{x \rightarrow 0}f(x)= lim_{x \rightarrow 0}g(x)=0$, is indeterminate. the limiting behavior of the mixture of the two functions (e.g., $lim_{x \rightarrow 0} x/x=1$, while $lim_{x \rightarrow 0}x^2/x=0)$ controls the value of the all-around limit.
There are seven indeterminate forms involving 0, 1, and infinity, stated as follows.
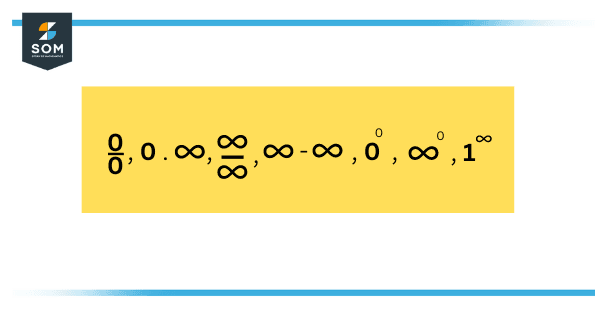
Figure 2 – Seven Indeterminate Forms
Importance of Indeterminate Forms in Calculus
If we dig better into the delicacies of indeterminate forms, we can realize how they can be used to define the attributes of any procedure at any given limit in any sort of way. The shortage of proper data demarcates an indefinite shape. Regardless, there is periodically too much information that entails lessening an answer to a distinctive strategy. Calculus is messed up with indeterminate forms.
In decree to decode for a limit when functioning with ratios like 1/0 and 0/0 or with an epoch of any kind, we will nearly definitely require to use another theorem, such as L’Hopital’s Rule. The reason that indeterminate forms are often resolvable is they can provide some light on a value that was formerly unidentified.
Assume the 0/0 fraction. Anybody with a primary knowledge of fractions would easily guess that this is equivalent to one as the numerator corresponds to the denominator, which is equivalent to one. A better applicable approach would be to presume that the fraction is zero thoroughly. Similarly, a zero in the denominator could illustrate infinity or the lack of anything.
As a consequence, there are multifarious categories for this ratio, but there is no clear conqueror. Then why are indeterminate forms needed in realistic-world scenarios? The clear answer to this problem is that they are not crucial at the smallest and not in seclusion. Nevertheless, their existence spreads the spadework for us to improvise new techniques to decode indeterminate forms.
Methods to Evaluate Indeterminate Forms
Following are the techniques that are used to solve the Indeterminate Forms.
Factoring Method
This procedure is commonly operated for 0/0 form, and it demands factoring the provided equations to their easiest forms. The limit value is used to solve after the most uncomplicated term has been emanated.
L’Hospital’s Rule
In the matter of an indeterminate form, the rule states that before applying the limit the best way to decode it is to distinguish the numerator and denominator separately. After each step, the products of the numerator and denominator are analyzed separately to inspect if they have become unrestricted of the variable, and as a result at least one of the terms remain constant or stable.
Division by Highest Power
When the indeterminate form is usually introduced in the / state, this methodology is generally utilized. In this procedure, dividing both the numerator and denominator of the given term by the most increased power variable in the sum is the most useful route of action. After this whole procedure, the limit value is decided.
Indeterminate Forms List
Examining all Indeterminate Forms on an individual basis below.
Indeterminate Form 1
Case: 0/0
Condition:
\[lim_{x \rightarrow c} f(x) = 0, lim_{x \rightarrow c} g(x) = 0\]
Transformation:
Transformation to ∞/∞. Then it transforms into:
\[ lim_{x \rightarrow c} \dfrac{f(x )}{g(x )} = lim_{x \rightarrow c} \dfrac{1/g(x )}{1/f(x )}\]
Indeterminate Form 2
Case: $\infty / \infty$
Condition:
\[lim_{x \rightarrow c} f(x) = \infty, lim_{x \rightarrow c} g(x) = \infty\]
Transformation:
Transformation to 0/0. After that, it becomes:
\[ lim_{x \rightarrow c} \dfrac{f(x )}{g(x )} = lim_{x \rightarrow c} \dfrac{1/g(x )}{1/f(x )}\]
Indeterminate Form 3
Case: $ 0 \times \infty$
Condition:
\[lim_{x \rightarrow c} f(x) = 0, lim_{x \rightarrow c} g(x) = \infty\]
Transformation:
Transformation to 0/0, which results in the following:
\[ lim_{x \rightarrow c} f(x )g(x ) = lim_{x \rightarrow c} \dfrac{f(x )}{1/g(x )}\]
Transformation to $\dfrac{\infty}{\infty}$, resulting in:
\[ lim_{x \rightarrow c} f(x )g(x ) = lim_{x \rightarrow c} \dfrac{g(x )}{1/f(x )}\]
Indeterminate Form 4
Case: $ 1^{\infty}$
Condition:
\[lim_{x \rightarrow c} f(x) = 1, lim_{x \rightarrow c} g(x) = \infty\]
Transformation:
Transformation to 0/0, after that, it becomes:
\[ lim_{x \rightarrow c} f(x )^{g(x )} = exp \space lim_{x \rightarrow c} \dfrac{lnf(x )}{1/g(x )}\]
Transformation to $\dfrac{\infty}{\infty}$, resulting in:
\[ lim_{x \rightarrow c} f(x )^{g(x )} = lim_{x \rightarrow c} \dfrac{g(x )}{1/lnf(x )}\]
Indeterminate Form 5
Case: $ 0^0$
Condition:
\[lim_{x \rightarrow c} f(x) = 0^+, lim_{x \rightarrow c} g(x) = 0\]
Transformation:
Transformation to 0/0, then it converts to:
\[ lim_{x \rightarrow c} f(x )^{g(x )} = lim_{x \rightarrow c} \dfrac{g(x )}{1/lnf(x )}\]
Transformation to $\dfrac{\infty}{\infty}$. It transforms into:
\[ lim_{x \rightarrow c} f(x )^{g(x )} = lim_{x \rightarrow c} \dfrac{lnf(x )}{1/g(x )}\]
Indeterminate Form 6
Case: $ \infty^0$
Condition:
\[lim_{x \rightarrow c} f(x) = \infty, lim_{x \rightarrow c} g(x) = 0\]
Transformation:
Transformation to 0/0. Then it develops into:
\[ lim_{x \rightarrow c} f(x )^{g(x )} = lim_{x \rightarrow c} \dfrac{g(x )}{1/lnf(x )}\]
Transformation to $\dfrac{\infty}{\infty}$. It turns into:
\[ lim_{x \rightarrow c} f(x )^{g(x )} = lim_{x \rightarrow c} \dfrac{lnf(x )}{1/g(x )}\]
Indeterminate Form 7
Case: $ \infty – \infty$
Condition:
\[lim_{x \rightarrow c} f(x) = \infty, lim_{x \rightarrow c} g(x) = \infty\]
Transformation:
Transformation to 0/0. Then it turns to:
\[ lim_{x \rightarrow c} (f(x )-g(x )) = lim_{x \rightarrow c} \dfrac{|1/g(x)| – |1/f(x)|}{1/|f(x) g(x)|}\]
Transformation to $\dfrac{\infty}{\infty}$, resulting in:
\[ lim_{x \rightarrow c} (f(x )-g(x )) = lim_{x \rightarrow c} \dfrac{e^{f(x)}}{e^{g(x )}}\]
Example of Solving an Indeterminate System
Consider the given expression:
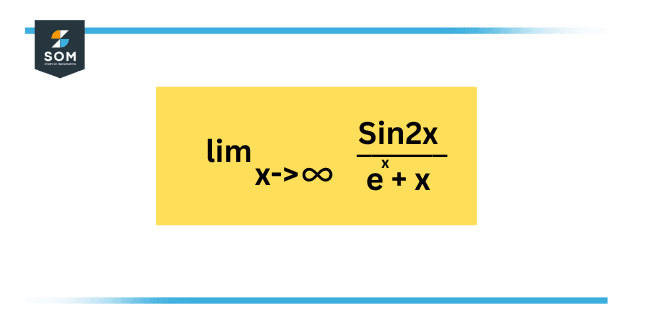
Figure 3 – An indeterminate system; the solution follows.
Solution
Let $f(x) = \sin(2x)$ and $g(x) = e^x +x$. Then:
\[ f'(x) = 2\cos(2x), \space g'(x)= e^x +1\]
\[ \lim{x \rightarrow 0} = \dfrac{f'(x)}{g(x)} = \lim{x \rightarrow 0} \dfrac{2\cos(2x)}{e^x +1}\]
Replacing limits:
\[ = \dfrac{2\cos(0)}{e^0 +1}\]
= 2/2 = 1
All images/mathematical drawings were created with GeoGebra.
