Index|Definition & Meaning

In mathematics, the exponent or power that is raised to a variable or a number is referred to as the index (or indices). Indices are the correct plural version of the word index. Both constants and variables are discussed in relation to algebra. 

A value that cannot be altered in any way is known as a constant, whereas a variable amount can have any number given to it, or its value can change depending on what we do with it. In algebra, we discuss indices in terms of the numbers that they refer to.

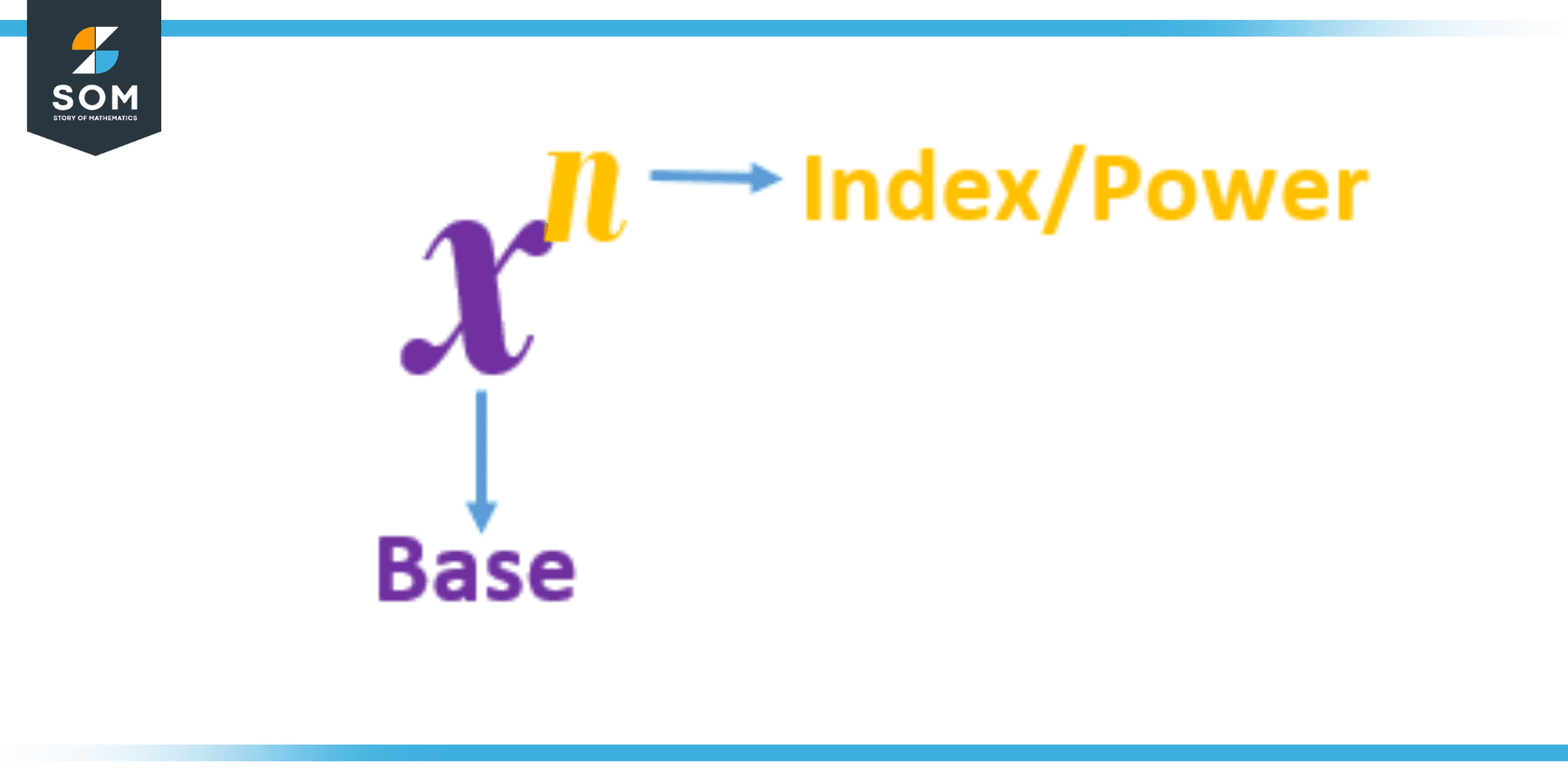
Figure 1 – Base and index

In mathematics, the term “index” can refer to a wide variety of different concepts. In the domain of an index set, it often refers to a quantity that can take on a range of values, and it is used to indicate one of a set of possible values for that quantity. As an illustration, the index of the symbol xⁿis the subscript n.

In economics, an index is a single number used to express an “average” value for a number of variables. A common name for it in this setting is “index number.”

Law of Indices

Indices are utilized to represent numbers multiplied by themselves. It can also be utilized to represent fractions and roots, such as a square root. The principles of indices make manipulation of expressions involving powers more efficient than putting them out in full.

Figure 2 – Index, Expanded, Numerical Form

There are fundamental norms or rules of indices that must be understood before we can begin dealing with them. These principles are utilized while conducting algebraic operations on indices as well as when solving algebraic expressions, which include it.

A collection of fundamental guidelines that define how indices are to be treated mathematically are known as the laws of indices. These rules are extremely important because indices have a purpose other than simply making it easier to write numbers numerically.

Rule 1

If a variable or constant has a value of ‘0‘ for its index, the result will then be equal to one regardless of the base value.

x⁰= 1

Rule 2

If the index is negative, it can be represented as the inverse of the positive index multiplied by the same variable.

x^-p= 1/x^p

Rule 3

When two variables are multiplied with the same base, their powers must be added and raised to that base.

x^p . x^q = x^{p + q}

Rule 4

When two variables are divided with the same base, we must subtract the power of the denominator from the power of the numerator and then raise the result to the same base.

x^p / x^q = x^{p – q}

Rule 5

When a number or variable with an index is again raised with another index then both the indices are multiplied in the power of a single base of that corresponding variable.

(x^p)^q= x^pq

Rule 6

When two variables with different bases but the same indices are multiplied together, their bases must be multiplied and the same index must be raised for both variables.

x^p . y^p = (xy)^p

Rule 7

When two variables with different bases but identical indices are divided, the bases must be divided and the index must be raised to it.

x^p / y^p = (x/y)^p

Rule 8

A representation of an index that has the form of a fraction can be made using the radical form.

x^p/q = $\displaystyle\mathsf{\sqrt[q]{x^p}}$

In mathematics, indices are a useful tool for compactly expressing the operation of raising or reducing a given number. A number can be multiplied with itself repeatedly to get power, whereas a fractional exponent of the number can be obtained by taking a root. As a result, it’s critical to comprehend both the concept and the rules of indices in order to apply them subsequently in significant applications.

Figure 3 – Law of Indices

In mathematics, indices are a useful tool for explaining how to raise or decrease a value to a degree or root. A number’s root is equivalent to its fractional power, but a number’s power is equivalent to repeatedly multiplying the original number by itself. You can develop a single measurement of change for many different items by estimating index numbers.

The calculation of the Index Price can be done using numbers, quantities, volume, and other elements. The computations also demonstrate the need for caution when interpreting index numbers. Critical factors to take into account are the items that need to be covered and the base time selection. It is impossible to overestimate the significance of the index numbers.

Examples of Index

Example 1

If the bases are the same, their powers will add.

In the first bracket, x has the power of 5. It will be solved with the x of the second bracket, which has nothing in power means it has 1 in power. x will be solved like this x⁵⁺¹ because the base x is the same, so power will add it will become x⁶.

The second variable is y; the powers of y are also added because bases are the same it will become y⁶.

The last variable is z and ends up as z⁴.

Example 2

All the figures above are created on GeoGebra.

Indeterminate Definition < Glossary Index > Infinite Definition