Infinite|Definition & Meaning

Infinity has no end, and infinity cannot grow or shrink. They are always infinite and last forever. You might think that infinity is something that does not exist or is not absolutely possible in real life, and is a concept invented by mathematicians and physicists. 

Time goes on forever, and if you travel in a spaceship for years, even after passing through every galaxy in existence, you’ll find nothing but a vacuum and empty space. The universe will still go on forever (at least that seems to be the theory of many astrophysicists!).

Figure 1 – Infinity on the real line

Figure 1 illustrates the infinity on a real line the arrow on both sides shows the positive and negative infinity.

Both a number and a very huge amount are not true of infinity. Infinity is actually a notion, not a property of a specific mathematical or physical substance. We cannot conceive of an endless number since it has no limitations.

For instance, by adding infinitely many various sizes of infinite sets, the mathematical idea of infinity expands and refines the traditional philosophical definition. The axiom of infinity, which ensures the existence of infinite sets, is one of the axioms of Zermelo-Fraenkel’s set theory, which may be used to build much of modern mathematics. Even in seemingly unrelated fields like combinatorics, the mathematical notion of infinity and the manipulation of infinite sets are employed all across mathematics.

For instance, in order to resolve a long-standing issue that is expressed in terms of simple arithmetic, Wiles’s proof of Fermat’s Last Theorem indirectly depends on the existence of very large infinite sets.

Infinity in Mathematics and Physics

Mathematics also contains infinities. For instance, the set of all natural numbers, or the numbers starting with 1, 2, 3, and so on, is infinite because there is always a number that is bigger than the one before it. The set of natural numbers is endlessly huge, one that we cannot measure, and it is crucial to note that infinity is not a very, very large number but rather that being infinite means that we can never stop counting them.

An immeasurable item that is constantly bigger than all others is infinity. Infinities cannot increase in size or decrease in size because they have no limit; they are constantly endless and continue forever. We could believe that infinity is a notion created by mathematicians and physicists and that it has no real-world use.

The most obvious manifestations of infinity, however, are space and time, in which we truly reside. Time continues to advance indefinitely, and if we board a spacecraft and travel for a very long time, even after we have passed all known galaxies, all we will encounter is a vacuum and empty space.

Symbol of Infinity

English mathematician John Wallis devised the mathematical sign for infinity in 1657. Infinity may be classified into three categories: mathematical, physical, and metaphysical. To represent the sizes of sets like the set of natural numbers, the set of points on the real line, and many others, the infinity sign is directly used in mathematics.

The lemniscate, often known as the infinity sign, is a mathematical symbol used to depict the idea of in the finite. Instead of referring to an actual infinite quantity like the ordinal and cardinal numbers, the symbol of infinity is more frequently employed to denote a prospective infinity. For instance, in the summation and limit notation of mathematics.

Properties of Infinity

Following are the Properties of infinity

• Associative Property
• Multiplication Property

Associative Property

The addition of infinity with any number will result in infinity:

$\infty$ + $\infty$ = $\infty$

-$\infty$ + (-$\infty$) = -$\infty$

Multiplication Property

Multiplication of any number with infinity will result in infinity:

$\infty \times \infty$ = $\infty$

-$\infty \times \infty$ = -$\infty$

-$\infty \times{}$(-$\infty$) = $\infty$

Additional Properties

If infinity is added or subtracted with any integer value y, then the result will be infinity:

 y + $\infty$ = $\infty$

y + (-$\infty$) = -$\infty$

However, infinity is the mental representation of such a numberless number in mathematics. The phrase “an infinite number of words” is sometimes used to refer to it as if it were a number that counts or measures things, even though it is impossible to finish counting these things in a finite amount of time. Therefore the phrase represents “an infinite number of terms, but not the same type of number as natural or real numbers.”

Infinity in Geometry

Infinity was very occasionally brought up in geometry until the very end of the 19th century, and only in relation to processes that had no end. For instance, a line was what is today referred to as a line segment, with the restriction that it can be extended as far as one likes, but the limitless extension was not possible. Similar to this, a line was often thought of as a possible site for a point rather than as being made up of an unlimited number of points. Only a finite number of points could be aligned on a line, despite there being an endless number of potential placements.

Projectile geometry was one of the few instances of a mathematical notion incorporating actual infinity. It models the perspective effect that seems to show parallel lines meeting “at infinity” by adding points at infinity to Euclidean space. Points at infinity have the benefit of allowing one to ignore some exceptional instances in mathematics.

For instance, on a projective plane, two unique lines meet at exactly one point, but there are no intersection places for parallel lines in the absence of points at infinity. Thus, in classical geometry, parallel and non-parallel lines must be examined individually, but they do not need to be differentiated in projectile geometry.

Infinite Dimension in Vector Spaces

Whenever they appear in classical geometry, vector spaces have a finite dimension, usually two or three. However, the abstract definition of a vector space does not imply this, and vector spaces of unlimited dimensions can be taken into consideration. This is frequently true in functional analysis, where function spaces are typically infinite-dimensional vector spaces.

Some topological constructs have the ability to produce topological spaces with infinite dimensions. This is especially true for iterated loop spaces.

Infinity Functions

Figure 2 illustrates the exponential function, which becomes infinite.

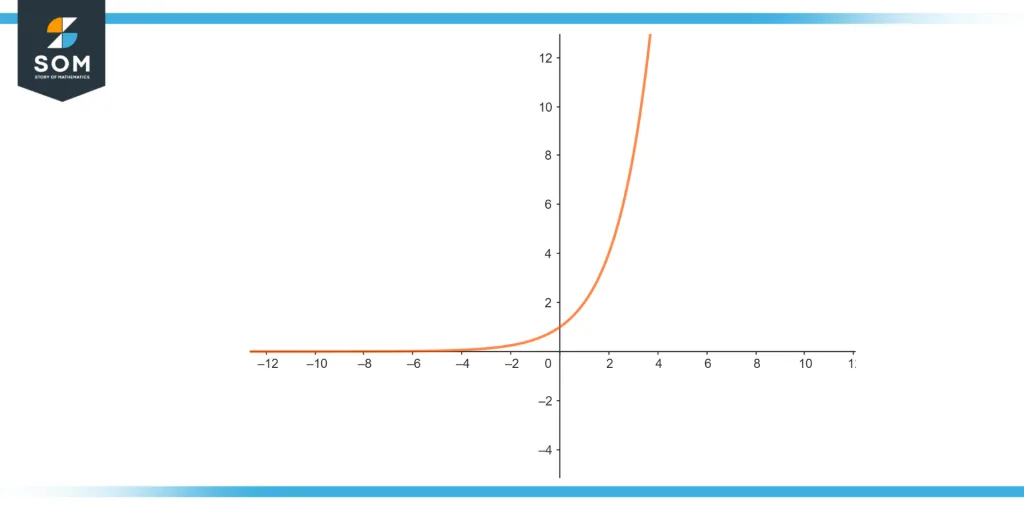
Figure 2 – Exponential function

Figure 3 illustrates $\frac{1}{x}$ which become infinite with increase in value of x

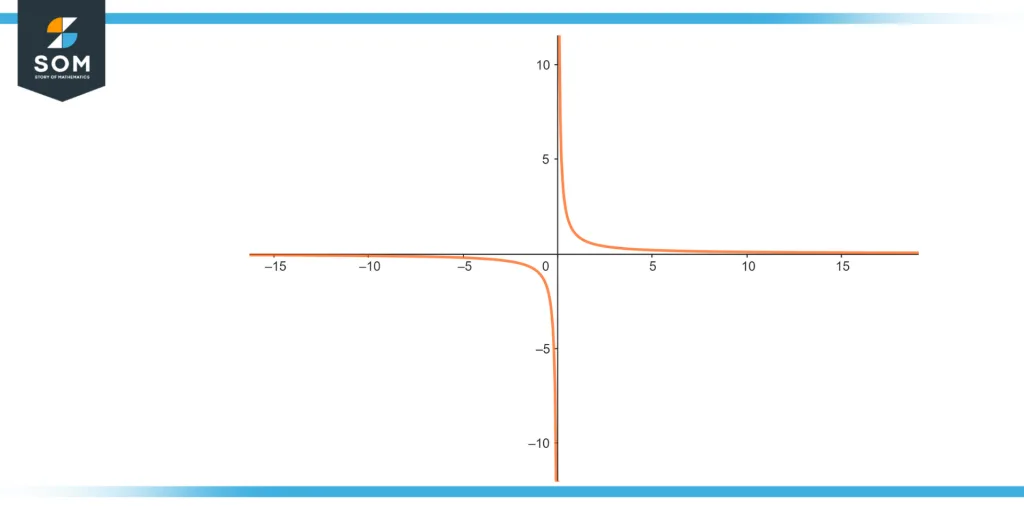
Figure 3 – Infinite function

Some Examples of Infinity

Example 1

Check whether the following series is infinite or not.

1. {1,2,3,4,…}
2. {2,4,6,8}

Solution

1. As {1,2,3,4, …} is endless series, so the given sequence is infinite.
2. As {2,4,6,8} is finite series, so the given sequence is finite.

Example 2

Check whether 0.500000000… is finite or not.

Solution

0.500000000… is continuous and endless, so it is infinite.

All images/mathematical drawings were created with GeoGebra.

Index Definition < Glossary Index > Inscribed Angle Definition