Inscribed Angle|Definition & Meaning

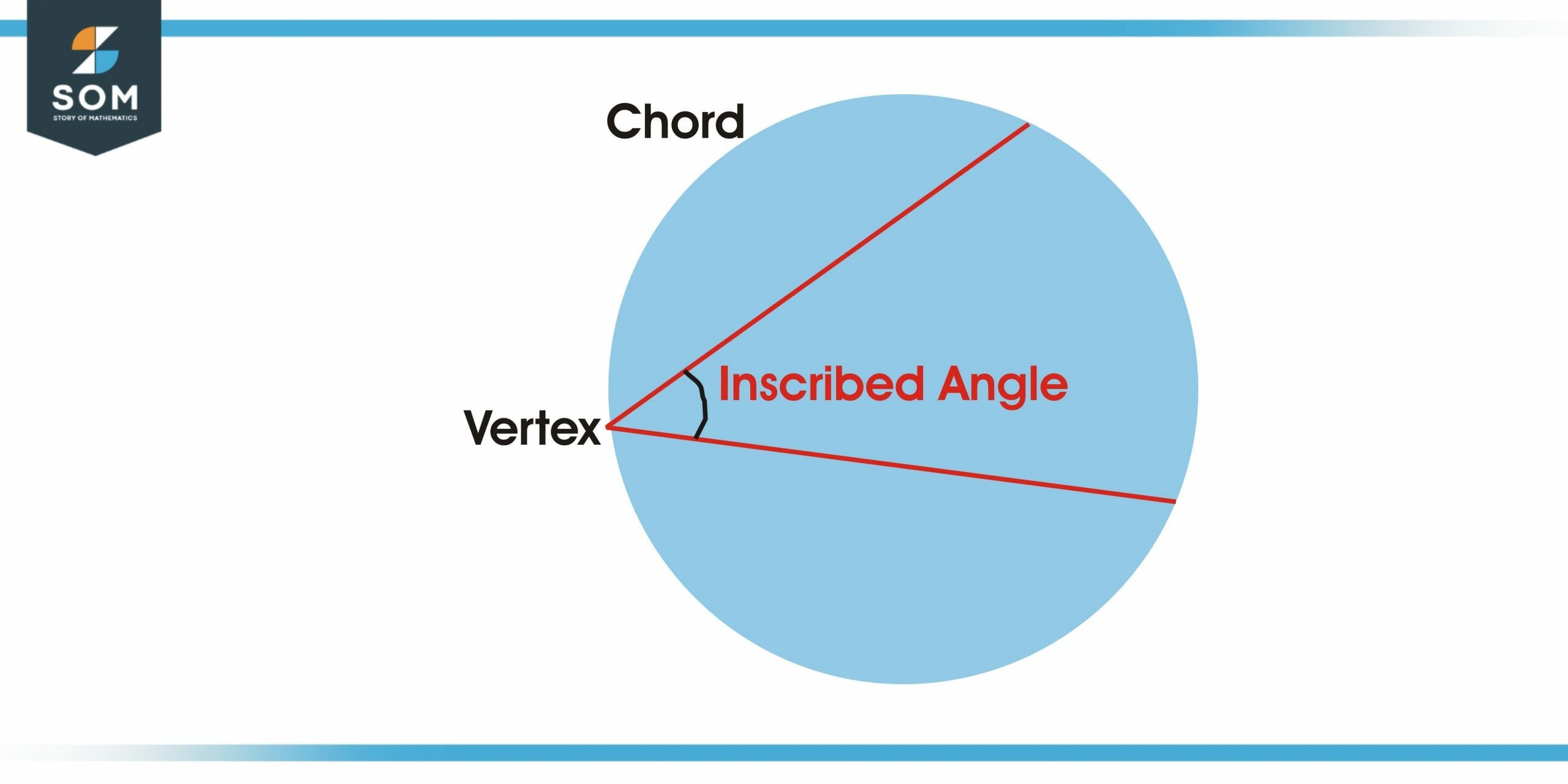
Figure 1 – Labelled Diagram of a Circle with an Inscribed Angle 

The other end of the inscribed angle is across the circle. Intercepted arc is an arc that is formed by the inscribed angle. The part of the circle’s circumference between the two chords of the inscribed angle is known as the arc. There is a unique relationship between the intercepted arc and the inscribed angle.

What Is an Angle, a Circle, and Central Angle?

An angle is a diagram or a figure that has two rays meeting at a single common point. The point where the two rays meet is known as the vertex. “∠” symbol is used to represent the angle.

A circle is defined as a plane mathematical figure that has an infinite number of points that are equidistant from a fixed point origin, that is the center of the circle. The outer boundary of a circle is known as the circumference and the distance from the origin to the circumference of the circle is known as the radius. The line meets two points on the circumference of the circle passing through the center of the circle is known as the diameter.

An angle whose vertex lies on the origin or center of the circle and its sides meet the circumference of the circle at two distinct points is known as the central angle of the circle.

The Measure of the Inscribed Angle – Inscribed Angle Theorem

The measure of the inscribed angle is half the measure of the intercepted arc of the inscribed angle. The inscribed angle whose measure is known to us, we can easily find the measure of the intercepted arc. Similarly, if the measure of intercepted arc is given, we can find the inscribed angle.

Let’s understand the measure of inscribed angle with examples. For the given figure we can see that the intercepted arc is 50 degrees. We know that an inscribed angle is half of the measure of an intercepted arc angle. So, in this case, the inscribed angle will be half of 50 which is equal to 25.

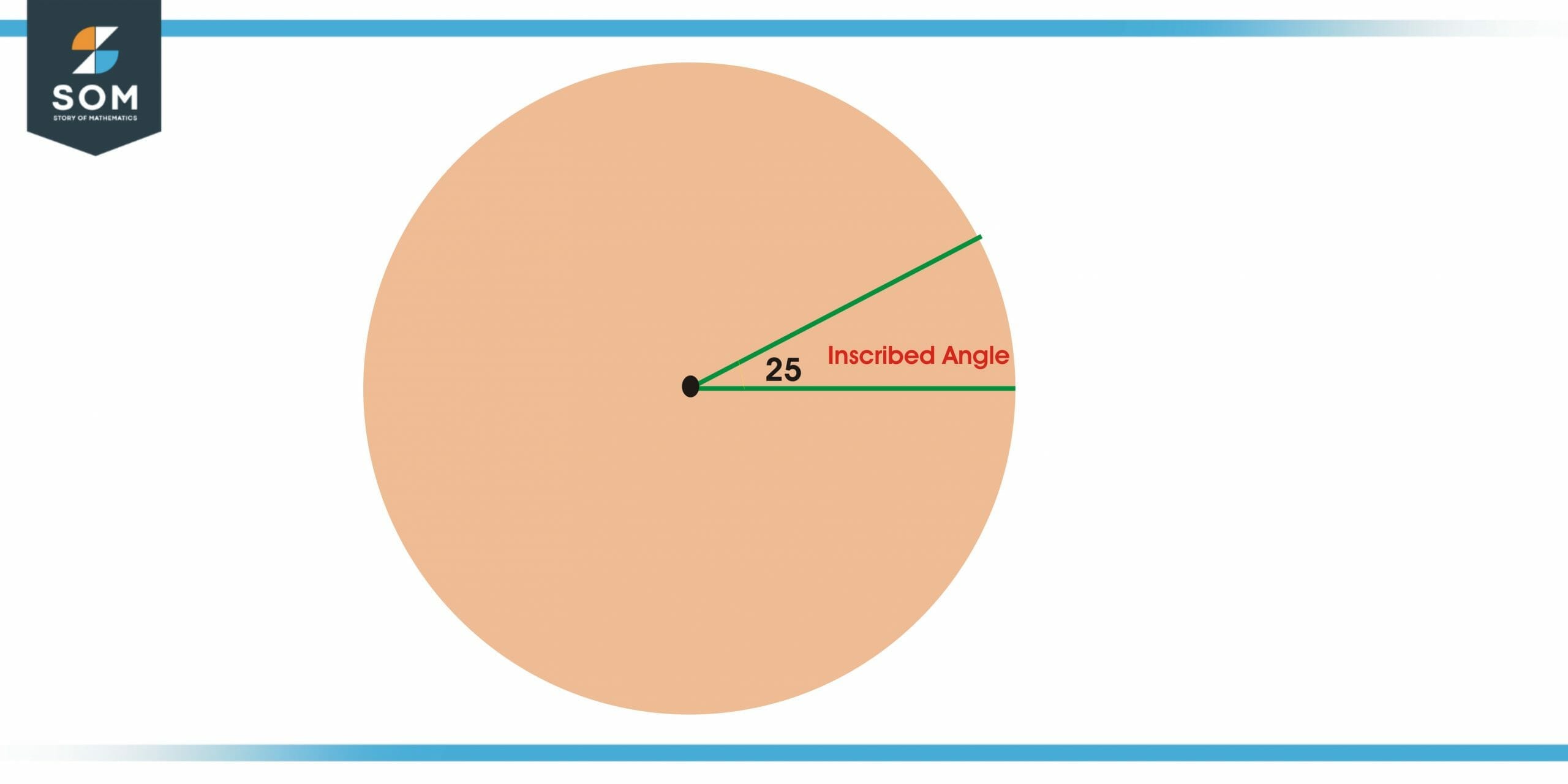
Figure 2 – Inscribed angle is 25 degrees

Now in another figure, we can see that we are given a circle in which there is an inscribed angle equal to 24 degrees. From this, we can find the intercepted arc measure because we know that the intercepted arc measure is double the measure of the inscribed angle. So, in this case, the double of the inscribed angle will be 48 degrees which is the intercepted angle of the given circle.

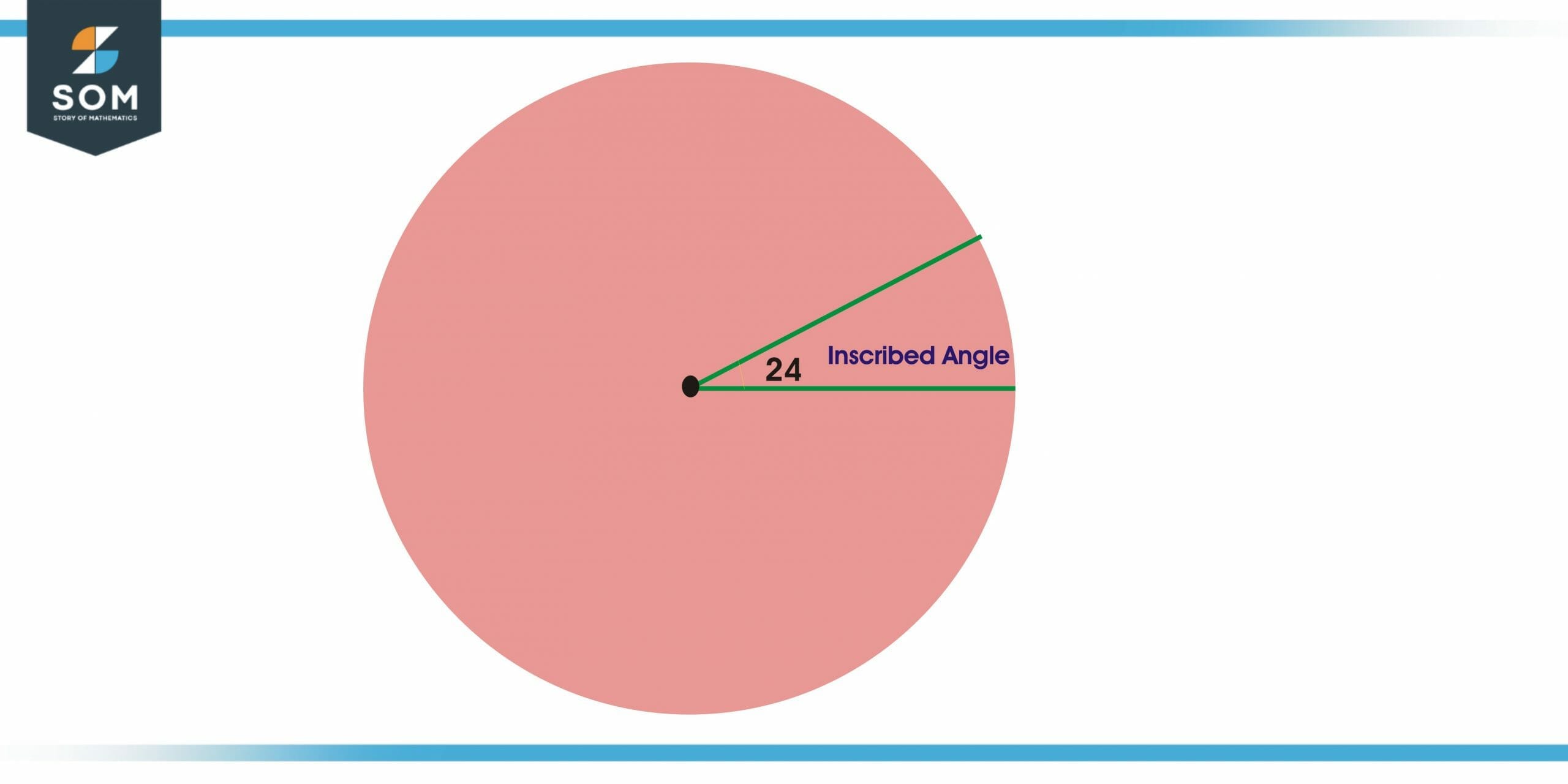
Figure 3 – Intercepted Angle in the circle

This measure is the Inscribed angle theorem. It is also called the arrow theorem or central angle theorem. The reason to call it the central angle theorem is that the inscribed angle is half the central angle whereas the central angle is always the same because the endpoints are fixed.

This theorem also states that the central angle is equal to double the inscribed angle subtended by the same arc. In other words, the inscribed angle is half the central angle for the same arc. Or, for the same arc, the central angle of the circle is double any angle formed at the circumference of that circle. These are all the statements for the inscribed angle theorem.

Properties of Inscribed Angle

Inscribed angles have the following properties with respect to the central angle of the circle.

For a single arc, the inscribed angles formed are always equal.

The inscribed angle formed is 90 degrees when in a semicircle.

The length of central angles formed by arcs is the same.

For a circle divided into four equal parts, the sum of opposite angles of the inscribed four portions is equal to 180 degrees.

The half of central angle gives the inscribed angle

Inscribed Polygon

A polygon whose all vertices lie on the outer boundary of a circle i.e. circumference is known as an inscribed polygon. The circle in which the polygon inscribes is known as a circumscribed circle.

Example Problems Involving Inscribed Angles

Example 1

The Central Angle formed by an arc of a circle is 74 degrees. Find the measure of the Inscribed Angle formed in the given circle.

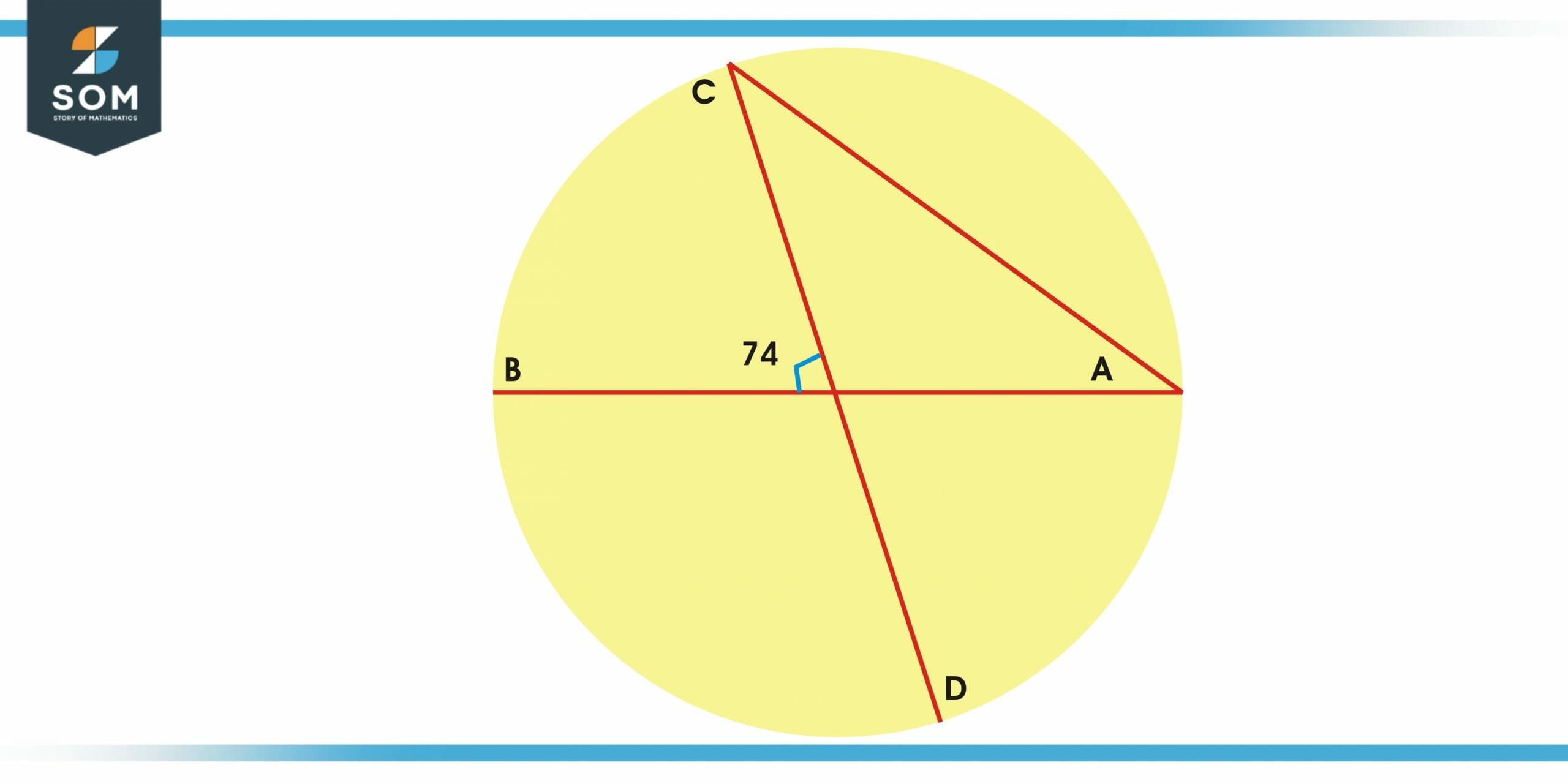
Figure 4 – Diagram for example 1

Solution

From the given figure we can say that the measure of the angle ACD is unknown.

Let O be the origin or midpoint of the given circle. Points CD and AB intersect with each other at point O. In the given figure, we can analyze that the inscribed angle is ACD because points A, C, and D are on the circle’s circumference.

As we discussed that the opposite angles in the circle with four parts are equal. So, in the given figure angle CMB and AMB are opposite to each other, so they have the same measure, which is 74 degrees. 

It is obvious that angle AMD is the central angle formed by the same arc as angle ACD. We know that according to the theorem of inscribed angle, half of the central angle for the same arc gives an inscribed angle. So:

Measure of angle ACD = Measure of angle AMD / 2 = 74 / 2

Measure of angle ACD = 37 degrees.

Hence the inscribed angle for the given central angle of the circle is 37 Degrees.

Example 2

Find the inscribed angle subtended by the circle if its arc’s measure is 140 degrees. Given that: BAC = (a + 15)

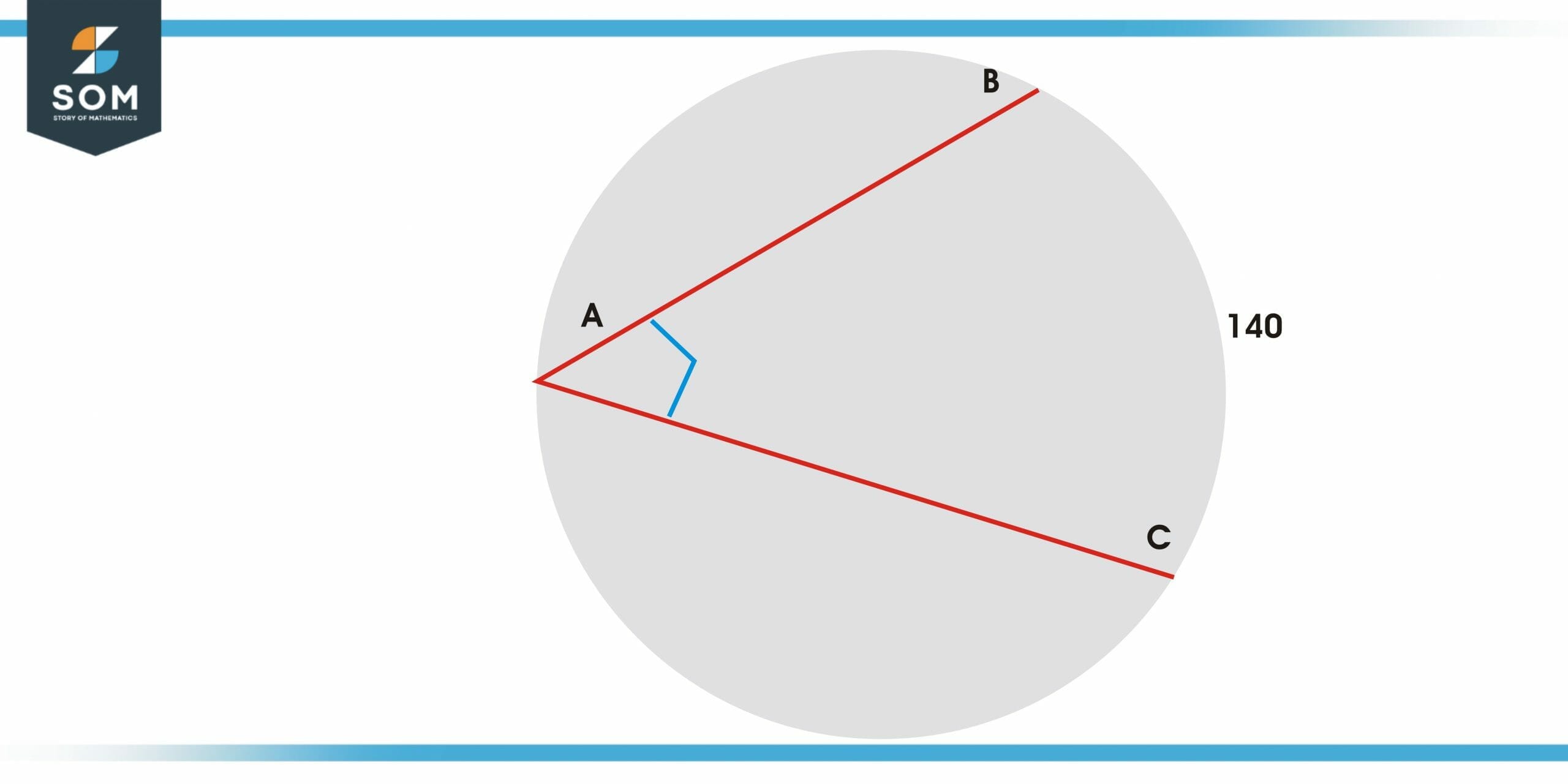
Figure 5 – Diagram for example 2

Solution

From the given figure, we are given:

Measure of angle BAC = ( a + 15 ) degrees

We need to find the value of a. In the given figure, the inscribed angle is BAC on the arc BC whose measure is given i.e., 140 degrees.

We know that according to the theorem of inscribed angle, half of the central angle for the same arc gives an inscribed angle.

So:

Measure of angle BAC = Measure of arc BC / 2

Measure of angle BAC = 140 / 2

Measure of angle BAC = 70 degrees

As we are given that:

Measure of angle BAC = ( a + 15 ) degrees

So:

a + 15 = 70

a = 70 – 15

a = 55

All the mathematical images are generated using GeoGebra.

Infinite Definition < Glossary Index > Interest Definition