Intersect|Definition & Meaning
Definition
The term “intersect” can be defined for both lines and sets. When we talk about an intersection in geometry, we mean that something cuts or passes through or across something.
When we talk about the intersection of two sets, we mean the set of shared elements between them.
Intersecting Lines
The meeting of any number of lines (must be more than one) is referred to as an intersection of those lines. That is, any number of lines that cross each other at a certain point are called intersecting lines. Such a case is illustrated in Figure 1 for two lines.
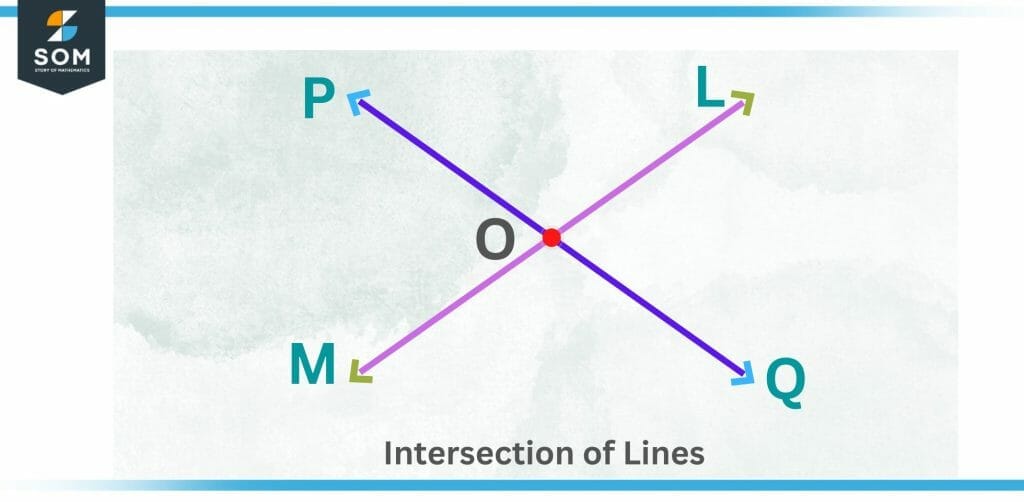
Figure 1 – Intersection of lines at point o
On the other hand, non-intersecting lines are those that never cross each other. By the definition of a line, two lines parallel to each other are an example of non-intersecting lines.
By its definition, the concept of intersection only applies to a group of geometrical objects. That is, we must have at least two geometrical objects to consider their intersection since the term is invalid for a single geometrical object.
Since intersecting lines meet at a point, it is possible for all the intersecting lines to meet at the same point or to cross each other at different points.
Lines, Line Segments, and the Point of Intersection
A line is defined as a figure with only one dimension in theory. Lines have an infinite length that is generally unmeasurable. However, a line segment is used to depict a finite line. A line segment has two endpoints, despite its appearance. Thus, a line segment has two endpoints, and its length can be measured.
The intersection of two or more line segments is referred to as a point of intersection. In light of the difference between lines and line segments, line segments may or may not intersect if they are not parallel because of their finite length. We cannot extend a line segment.
On the other hand, if any two lines are not parallel, their infinite length means that they will eventually cross at some point when extended on either side. Thus, even if two lines look like they do not cross on a given graph and scale, they intersect eventually if they are not parallel to each other.
In other words, lines are only truly non-intersecting when they are parallel to each other.
What Does It Look Like When Two Lines Intersect?
It is simple to determine whether or not the given figure of two line segments intersects. Two intersecting lines can look like the letters T or V. When two intersecting lines cross each other. They typically form an X.
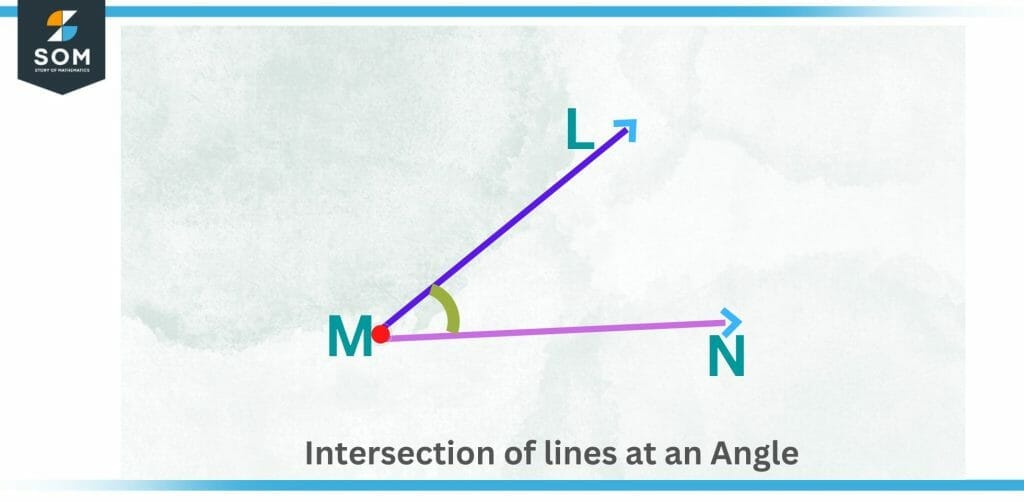
Figure 2 – Intersection of lines at an angle
This illustration shows how two intersecting lines meet at a single point. Understanding the preceding image makes identifying intersecting lines the next time you see it a breeze.
Two non-parallel line segments may not cross. They can, however, have an intersection point, such as the letter V.
When two intersecting lines are perpendicular to each other, they form the letter T. When two lines are perpendicular. They form a 90° angle at the point of intersection. It means that perpendicular lines intersect only at right angles.
How To Find the Point Where Two Lines Intersect?
To grasp how to find the intersection of two lines, consider two non-parallel lines. The images in Figures 1 and 2 depict two non-parallel lines intersecting at a specific point.
Just by looking at two lines, one can easily determine where they intersect. When two line segments intersect, they are referred to as two intersecting lines. It aids comprehension of how to find the intersection of two lines.
The following factors influence the intersection of two lines:
- The lines must be non-parallel to one another.
- The lines must be straight at the given point of intersection.
- Two lines must meet at the location where there is an angle between the two intersecting line segments.
- The absence of a point of intersection between two non-parallel lines does not imply that they are non-intersecting. It means that when these two line segments are extended on either side, they will eventually meet at some point, no matter how far apart they are.
How Do You Know if Two Lines Will Intersect or Not?
The preceding explanations demonstrate that parallel lines do not intersect. However, even the slightest tilt of either line can cause an intersection.
Even if two line segments appear parallel, they can still intersect when drawn forward or backward.
Even if two non-parallel line segments are not parallel, they are considered non-intersecting lines in some cases due to the large distance between them. It is meaningless to claim that two lines cannot intersect because they are so far apart.
These lines may have to travel a long distance to intersect. They are not, however, non-intersecting lines.
If two lines are non-parallel to each other and perpendicular to each other, they will intersect.
Set Intersection
For two given sets, the intersection of sets is the set that contains all of the elements that are shared by both sets. The intersection of sets is represented by the symbol “∩. “
The intersection, M ∩ N (read as M intersection N) of any two sets M and N, lists all of the elements that appear in both sets and are shared by M and N. A ∩ B = 6, 7, 8, if Set A = 6,7, 8, 9, 11, 12,13, and Set B = 5, 6, 7, 8.
Subsets
If set M consists of all possible natural numbers from 1 to 15, and set N consists of all possible odd numbers from 1 to 15, then N is a subset of M. A subset of the intersection’s two sets, (M ∩ N) ⊂ M and (M N) ⊂ N, is known as the intersection of sets.
M, for instance, is the set of elements 1 to 15. B = 2, 4, 7, 12, 14. Because of this, M ∩ N is a subset of both M and N.
Complement of Set Intersection
The set containing all elements in the universal set is the complement of the intersection of sets that are not in M ∩ N. If M = 1, 2, 3, 4, 5, and N = 2,4,6,8,10, and U = 1,2,3,4,5,6,7,8,9,10, then M ∩ N = 2,4 and ( M ∩ N)’ = 1,3, 5,6,7,8,9,10, respectively. (M ∩ N)’ is the complement of an intersection set.
Venn Diagram of Intersection Set
Venn diagrams make it simple to understand the intersection of sets. Circles are used to represent each set in Venn diagrams. Overlapping circles indicate that two or more sets have a relationship and share elements. And the circles that do not overlap have no elements in common.
The following Venn diagram depicts the intersection of two sets. Set Q equals 5, 6,7, 8, 9, 10, and Set P equals 2, 4, 6,8. As a result, Q ∩ P = 6, 8.
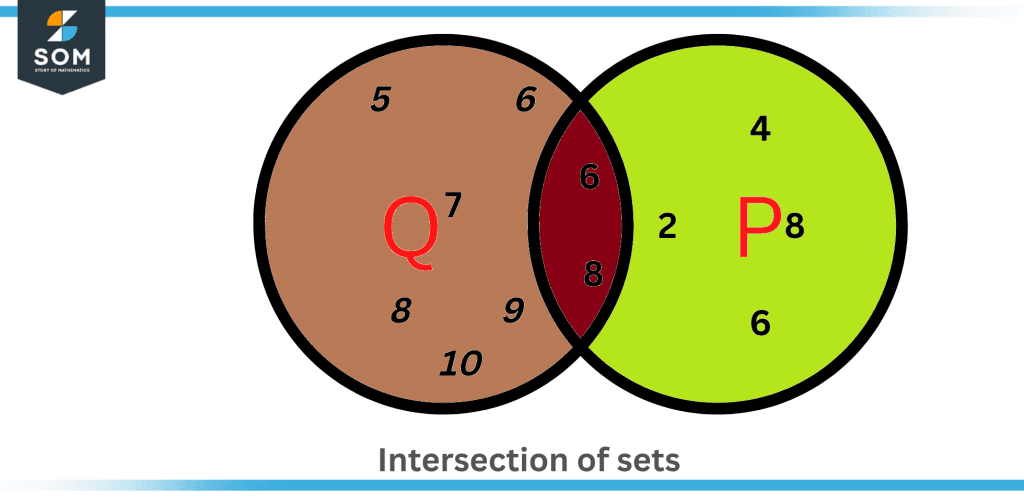
Figure 3 – Venn diagram of Intersection of sets
Examples of Real-Life Intersections
What are some examples of intersecting lines from real life?
Solution
Line intersections are a common occurrence in everyday life. Even if you don’t notice them, they are surrounded by intersecting lines.
A crossroads, for example, is a location where two roads intersect at a common point. This example indicates that the two roads are not parallel. Apart from that, at their intersection, these two roads form a specific angle.
A pair of scissors is yet another example. The two scissors knives are analogous to two intersecting lines. The two knives, when held apart, make an angle when two lines cross at a point of junction.
All images/mathematical drawings were created with GeoGebra.
