Intersection|Definition & Meaning

What Is an Intersection? 

The word “intersection” is used frequently in various settings, ranging from intersectionality to actual physical intersections in the road. So, in mathematical terms, what does it mean to have an intersection? Take, for example, a traffic intersection, where the intersection itself is understood to be where two routes converge.

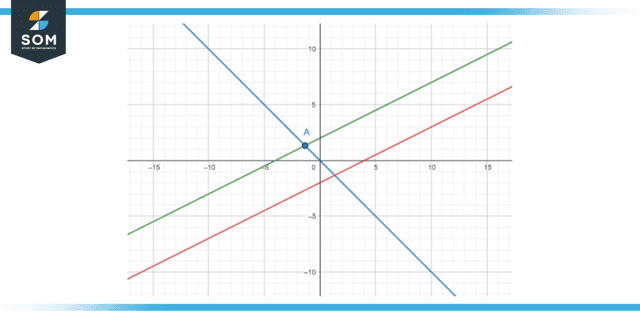
Figure 1: Intersection of lines. The blue line intersects the green one at point A and the red line at an unmarked point.

An Intersection in the Field of Geometry

When two or more geometric objects cross paths, this relationship is an intersection in geometry. One may also refer to this as a geometric junction. The meeting point of two straight lines is an example of a typical intersection in geometry. Take, for example, a busy crossroads with multiple lanes of traffic.

The point at which two roads cross one another and form an intersection is called the “intersection point.” If the roads are completely straight, then the only place where they will meet is at this particular intersection.

Similarly, the point at which two lines meet is referred to as the intersection of the lines, and lines that are characterized as intersecting lines are lines that do so in exactly one location.

What Do the U and Upside-down U Mean?

Because the U denotes the union of two sets, it follows that every object can be found in either one or both sets. The inverted letter U can symbolize the intersection of two sets or the subset of items present in both sets.

Symbolism and Significance of Lines That Cross One Another

A specific notation is known as the intersection symbol used to signify lines or sets that intersect.

Take note of how the green line and the red line do not overlap. Two lines that are parallel to one another look like this. Lines parallel to one another can continue into infinity in either direction, but they will never meet. Lines perpendicular to one another are other phrases that can represent line junctions.

The intersection of two lines that run perpendicular to one another results in the formation of a right angle. The lines in green and blue are said to be perpendicular to one another because, when they intersect, they produce right angles that measure 90 degrees.

The Intersection of Lines and Shapes

It is optional for there to be two lines at a geometric intersection. A line can intersect with other objects, like shapes. This is shown in figure 1 at the top of this page. At points A and B, the green circle can be seen to be intersected by the blue line. Keep in mind that there is only one location where two lines can meet.

On the other hand, a shape can have multiple lines intersect at multiple points. At Two Points, a Straight Line Cuts Across a Circle. Furthermore, shapes can intersect with one another, and these intersections can take place at multiple points.

Intersection of Planes

The intersection of two planes is yet another fascinating example of geometric intersection. When two planes meet, their intersection does not look like a point or a collection of points; instead, it is a straight line.

Consider this situation as though you were looking at two sheets of paper that crossed over each other—the point along the gap where they are numbered. Real numbers, odd numbers, prime numbers, and other types of numbers are examples of standard number sets. It’s also possible to have considerably smaller sets.

Mathematically speaking, how does one locate the intersection?

The point at which two mathematical objects overlap is their intersection.

The point or group of points at which two or more geometric objects cross is known as the intersection of those objects. The intersection of two sets is comprised of every number or object that both of those sets share. This can apply to numerical or non-numerical sets.

Example of an Intersection in Mathematics

In geometry, an intersection can be illustrated as a line that passes through a circle. The line intersects the circle in two different places: once when it is inside the circle and once when it is outside of it. The line and the circle meet at these two locations, constituting the intersection.

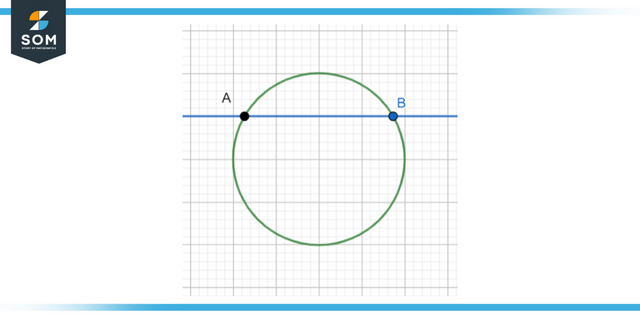
Figure 2: Line intersecting a circle at two points

What Does It Mean To Have an Intersection?

Where two things meet is referred to as their intersection. This is the point on a graph where two geometric objects cross each other. It represents the intersection of the two objects. In the context of sets, “intersection” refers to all the objects shared by two sets.

What Does It Mean When Two Planes Intersect?

Every pair of planes that is not parallel to another must necessarily intersect. At the point where they intersect one another, a straight line is formed. There will always be a line at any point where two planes meet.

Examples of Intersection

Example 1

Find the intersection of the following three sets: A ∩ B ∩ C

A = {1, 2, 4, 7, 23, 3, 50}

B = {2, 9, 21, 5, 7}

C = {12, 7, 14, 19, 3, 9}

Also draw the venn diagram to represent the elements.

Solution

The common element amongst the three sets is seven; therefore, the intersections A ∩ B ∩ C will become 7.

The Venn Diagram is Shown Below:

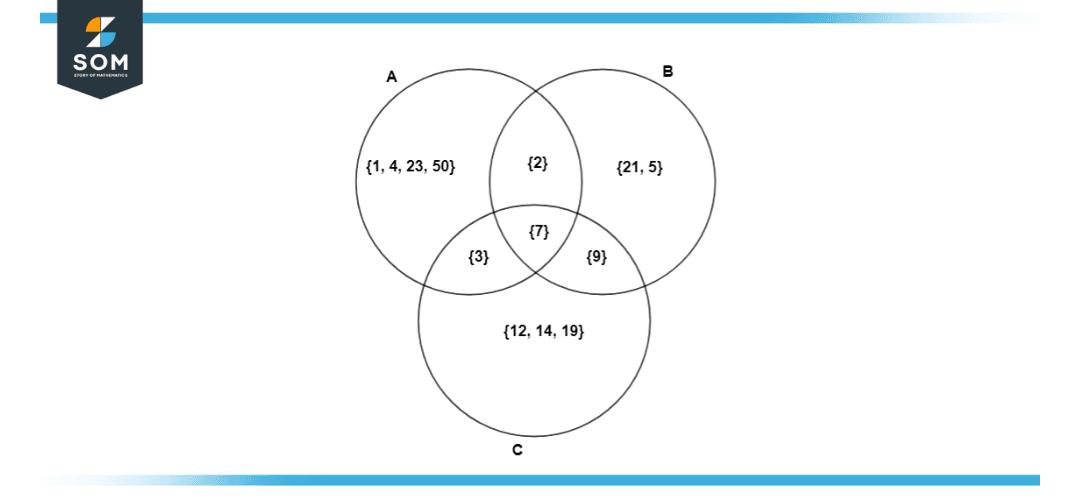
Figure 3: Venn Diagram for Example 1

Example 2

A line intersects a circle at point A (2, 5) and point B (1, 3). Find the midpoint between point A and point B.

Solution

To find the midpoint, the following formula is applied:

Midpoint = $\displaystyle \mathsf{\left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)}$

Here, x₁ = 2 | x₂ = 1 | y₁ = 5 | y₂ = 3

Substitute the values in the formula shown above:

\[ \mathsf{= \left( \frac{2 + 1}{2}, \frac{5 + 3}{2} \right)} \]

= (3/2, 8/2)

= (1.5, 4)

The midpoint becomes: (1.5, 4) for the given points.

All mathematical drawings and images were created with GeoGebra.

Intersect Definition < Glossary Index > Intersection Sets Definition