Intersection (Sets)|Definition & Meaning

If we refer to A as the set of odd numbers less than 10 and B as the set of the first five multiples of 5, we can determine the intersection of these two sets using the formulas provided below. 

A = {1, 3, 5, 9}

B = {5, 10, 15, 20, 25}

Five is the element that is shared by both A and B. As a result, the set of items that constitute the intersection of A and B equals 5.

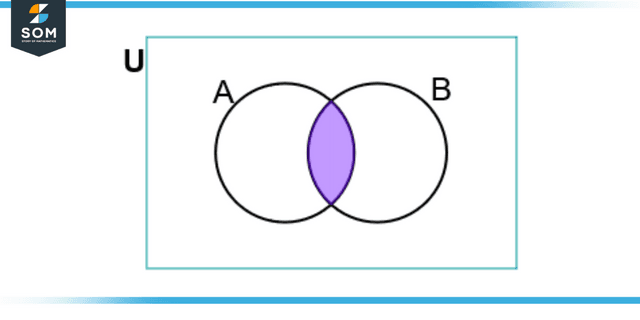
Figure 1: Representation of the intersection of 2 sets.

The Symbol for the Intersection of Sets

The sign “∩” can represent the overlap of sets as necessary. According to the definition given above, the set representing the intersection of 2 sets, A and B, is the collection of all of the elements shared by both A and B. We can use the notation A ∩ B to convey that A and B are connected in some way.

The Formula for A Intersection With B

The formula for finding where two sets intersect can be derived from the definition of the intersection. Therefore, the set that contains the elements that are identical to both A and B is the set that constitutes the intersection of the 2 sets, A and B.

The Intersection of Two and Three Sets

Two Sets

The most comprehensive set that includes all of the components shared by two sets, such as X and Y, is referred to as the intersection of those sets. The intersection of two sets may be another set with at least one element, or it may be an empty set, which means there are no elements in the intersection set.

Either way, the intersection set is considered a set. Assuming that A and B are two sets, and if the difference between A and B equals, we refer to A and B as disjoint sets. This indicates no component at the point where A and B cross.

Three Different Sets

It is possible to determine the point where more than two sets intersect with one another. You will learn how to locate the intersection of three sets in the next portion of this guide. When A, B, and C are three different sets, the set that results from the intersection of these three sets is the collection of all elements that are shared by all three sets.

This can be expressed using the notation A ∩ B ∩ C.. With the help of the example provided below, this can be understood more clearly.

For example, A = {4, 8, 10, 12}, B = {4, 9, 15, 18, 21, 24}, and C = {4, 8, 12, 18}.

Let us find out the common elements of the given sets.

4 is the only common element in A, B, and C. Therefore:

A ∩ B ∩ C = {12}.

Figure 2: Representation of the intersection of 3 sets.

Properties of Intersection of Sets

Some Properties of the Operation of the Intersection are listed below:

Commutative Law

A ∩ B = B ∩ A

Consider two sets A = { 2, 3, 4} and B = {2, 3, 5}.

Now:

A ∩ B = { 2, 3, 4} ∩ {2, 3, 5, 7} = {2, 3}

B ∩ A = { 3, 5, 7} ∩ { 3, 4, 5} = {3, 5}

Therefore:

A ∩ B = B ∩ A.

Associative Law

(A ∩ B) ∩ C = A ∩ (B ∩ C)

Let A = {, 3, 4}, B = {4, 5, 7}, and C = { 7, 8 }.

Now:

A ∩ B = {3, 4} ∩ { 4, 7, 8} = {4}

(A ∩ B) ∩ C = { 4} ∩ { 7, 8} = { } = φ

B ∩ C = { 4, 5, 7} ∩ { 7, 8} = {7}

A ∩ (B ∩ C) = {3, 4} ∩ {7} = { } = φ

Therefore:

(A ∩ B) ∩ C = A ∩ (B ∩ C)

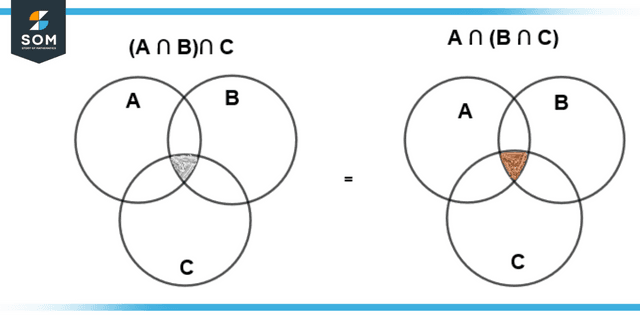
Figure 3: Associative Law

Idempotent Law

A ∩ A = A

Here:

A = {x,y,z} such that A ∩ A = {x,y,z} ∩ {x,y,z} = {x,y,z} = A

Distributive Law

 A ∩ (B U C) = (A ∩ B) U (A ∩ C)

Let us take three sets A = {2,3, 8}, B = {2,3, 7} and C = {3, 4, 5}.

B U C = {2,3,7} U {3, 4, 5} = { 3}

A ∩ (B U C) = {2, 3, 8} ∩ { 3} = {2, 6}

A ∩ B = {2, 3, 8} ∩ {2, 3, 7} = {2,3}

A ∩ C = {2, 3, 8} ∩ {3, 4, 5} = {3}

(A ∩ B) U (A ∩ C) = {2,3} U {3} = {3}

Hence proved.

Examples of Intersection in Sets

Example 1

List of students from grade 7 who chooses Mathematics as their favorite subject are:

John, Elsa, Harry, Emma, Robin, Nancy, Will, Mike and Steve

List of students from grade who chooses Science as their favorite subject are:

Emily, Carla, Samuel, Lucas, Harry, Steve, Elsa, Anna and Tyler

Students that chooses both Mathematics and Science as their favorite subjects are?

Solution

Let S1 = {John, Elsa, Harry, Emma, Robin, Nancy, Will, Mike, Steve}

Let S2 = {Emily, Carla, Samuel, Lucas, Harry, Steve, Elsa, Anna, Tyler}

S1 ∩ S2 = {Harry, Steve, Elsa}

Example 2

A school has organized a football and cricket tournament.

Students that got selected for football team were:

Noah, Leo, Ivan, Justin, Kim, Wade, Guzman, Drake, Oliver, George, David and Alex

Students that got selected for cricket team were:

James, Robert, Ivan, Harvey, Tom, Patrick, David, George, Tyler, Jack, Matthew and Oliver

How many got selected for both teams?

Solution

Let H1 = {Noah, Leo, Ivan, Justin, Kim, Wade, Guzman, Drake, Oliver, George, David, Alex}

Let H2 = {James, Robert, Ivan, Harvey, Tom, Patrick, David, George, Tyler, Jack, Matthew, Oliver}

H1 ∩ H2 = {Ivan, David, George, Oliver}

All images/graphs are created using GeoGebra.

Intersection Definition < Glossary Index > Invariant Definition