Invariant|Definition & Meaning

A graphical elaboration on invariant has been elaborated in Figure 1 below: 

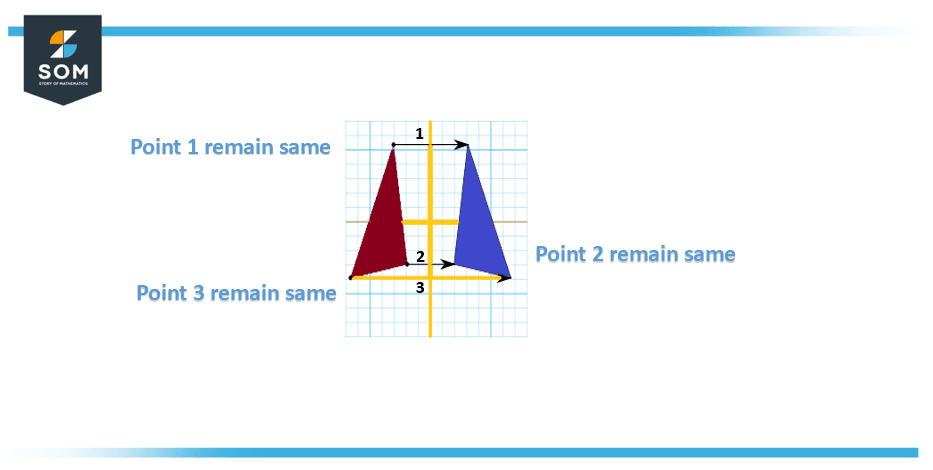
Figure 1: Concept of invariant

In other words, an invariant in mathematics is a property or value that remains unchanged under a set of transformations or operations. It is a feature of a system that is constant and can be used to make general statements and predictions about the system’s behavior.

Invariants play an important role in simplifying and understanding complex mathematical structures.

The basic idea of an invariant is that it is a property or feature of a system that remains constant, regardless of the specific details or transformations of the system. The purpose of this concept is to identify and understand these constant properties, which can then be used to make general statements and predictions about the system as a whole.

Invariants are useful in many areas of mathematics, including algebra, geometry, and physics, as they allow for simplification and a deeper understanding of complex systems.

Applications of Invariant

Invariant has many applications in various areas of mathematics and physics, including:

Algebra

Invariants are used to study algebraic structures, such as groups and rings. For example, the dimension of a vector space is an invariant that remains constant under a change of basis.

Geometry

Invariants are used to study geometric shapes and figures. For example, the area of a triangle is an invariant that remains constant regardless of the specific coordinates of the triangle’s vertices. Following Figure 2 shows that the rotation operation does not affect the invariance of the geometry.

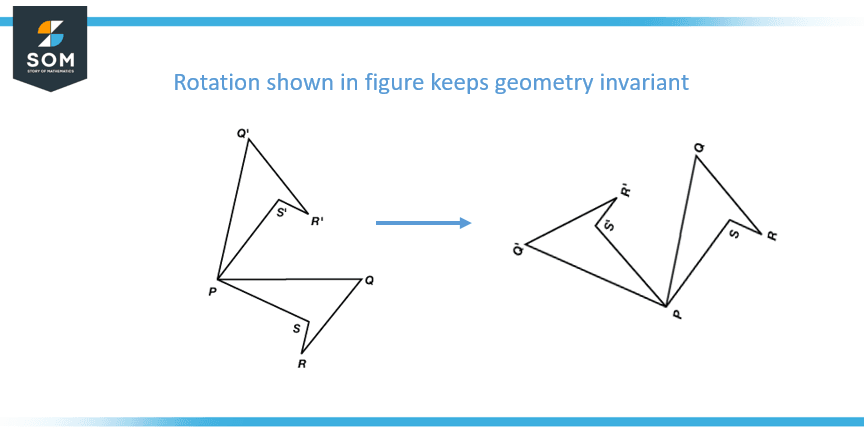
Figure 2: Rotation operation effect on invariance

Physics

Invariants are used in physics to study the symmetries of physical systems. For example, the energy of a system is an invariant that remains constant under certain transformations, such as translation in space and time.

Control Theory and System Identification

Invariants are used to identify the underlying dynamics of a system and to design control laws that are robust to parameter variations and disturbances.

Computer Vision and Image Processing

Invariants are used to recognize and match patterns and shapes in images, regardless of their position, orientation, and scale.

Robotics

Invariants are used to design control laws that are robust to uncertainty and sensor noise.

Machine Learning and Pattern Recognition

Invariants are used to extract features that are robust to variations in the data and to classify and cluster patterns and shapes.

Uses of Invariant in Real Life

Invariants are used in many everyday applications, some of which include:

Computer Vision

Invariant features such as SIFT and SURF are used in image and object recognition to identify and match patterns and shapes in images, regardless of their position, orientation, and scale.

Robotics

Invariants are used in the control and navigation of robots, allowing them to adapt to changes in their environment and perform tasks despite uncertainty and sensor noise.

Face Recognition

Invariant features such as eigenface and fisher face are used in face recognition systems to identify individuals regardless of facial expressions or lighting conditions.

Fingerprint Recognition

Invariant features such as minutiae points are used in fingerprint recognition systems to identify individuals regardless of the angle or pressure of their fingerprints.

Speech Recognition

Invariant features such as Mel-frequency cepstral coefficients (MFCC) are used in speech recognition systems to identify speech patterns regardless of the speaker’s voice or accent.

Machine Learning

Invariant features such as PCA and LDA are used in machine learning to extract features that are robust to variations in the data and improve the performance of classifiers and clustering algorithms.

Navigation Systems

Invariant features such as a Global positioning system (GPS) are used in navigation systems to provide location information regardless of weather conditions and atmospheric disturbances.

In general, the concepts of invariants are used in many systems in order to make them robust to changes in the environment and the input.

Types of Invariant Sets

An invariant set, also known as an attractor or a stable set, is a subset of the state space of a dynamical system that remains unchanged under the dynamics of the system. In other words, if a point in the state space of a system is in an invariant set, it will remain in that set for all future time steps.

Different invariant transformations do not affect the basic shape of the function, this is shown in figure 3 below:

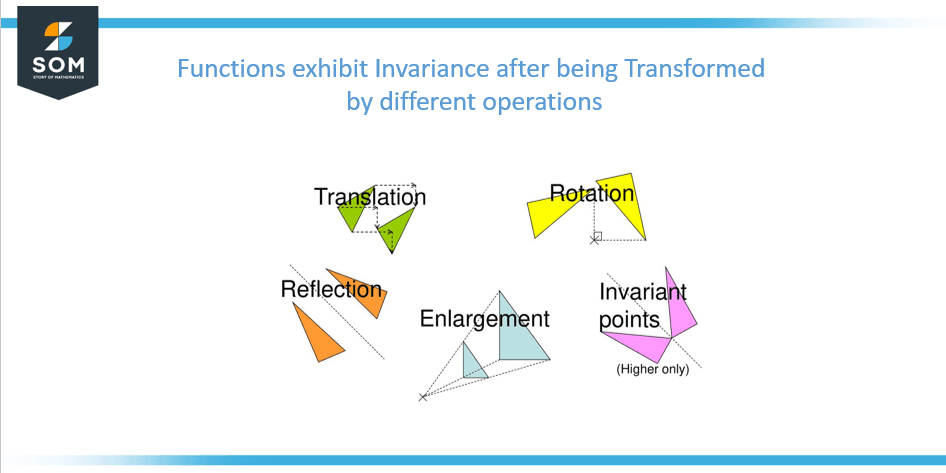
Figure 3: Effect of invariant transformations on functions

Invariant sets can be classified into two categories:

Attractors

These are invariant sets that are attracted to by nearby states. They are typically the endpoints of the dynamics of the system. Examples of attractors include fixed points, limit cycles, and strange attractors.

Repulsors

These are invariant sets that repel nearby states. They are typically the starting points of the dynamics of the system. Examples of repulsors include saddle points, unstable manifolds, and unstable periodic orbits.

Invariant sets play an important role in the study of dynamical systems and are used to classify and understand the long-term behavior of the system. They are used in many areas of mathematics, physics, and engineering, including control theory, computer vision, and robotics.

Invariant in Perturbation

In perturbation theory, an invariant is a property or quantity that remains unchanged under the effect of small disturbances or perturbations. Perturbation theory is a mathematical technique used to study systems that are slightly different from a known, well-understood system.

An example of an invariant in perturbation theory is the first-order invariant, which is a property or quantity that is unchanged from the first-order in the perturbation parameter.

For example, in celestial mechanics, the position of the planets in their orbits is invariant to first-order in the perturbation parameter, which is the ratio of the gravitational force between the planets and the central force.

Another example is in Quantum mechanics, the energy levels of an unperturbed Hamiltonian are invariant to first-order in the perturbation parameter. The eigenvalues of the unperturbed Hamiltonian remain unchanged, and the eigenvectors of the unperturbed Hamiltonian are only slightly modified by the perturbation.

Invariants in perturbation theory are useful for making approximations and predictions about the behavior of a system when it is subject to small disturbances. They can also be used to simplify the mathematical analysis of a system and to identify the key features of a system that are most affected by perturbations.

Solved Examples of Invariant Concept

Example 1

Give an example of an invariant operation in mathematics.

Solution

An example of an invariant from mathematics is the commutativity of addition in a set of integers. The property that

a + b = b + a for any two integers a and b

is invariant under the operation of addition. This property remains true regardless of the specific values of a and b.

Example 2

Is the Pythagorean Theorem an example of invariance?

Solution

Yes, the Pythagorean Theorem in Euclidean geometry, which states that in a right triangle, the sum of the squares of the lengths of the two legs is equal to the square of the length of the hypotenuse, is an example of invariance. This theorem is invariant under translation, rotation, and reflection.

Example 3

Discuss the invariance of Noether’s Theorem from physics.

Solution

In physics, Noether’s Theorem is an example of invariance. Noether’s Theorem relates the symmetries of a physical system to its underlying physical laws. It states that for every continuous symmetry of a physical system, there is a corresponding conserved quantity.

For example, the conservation of energy in a system is a direct result of the time-translation symmetry of the system.

Example 4

In algebra, does the Gaussian elimination method demonstrate invariance?

Solution

Yes, the Gaussian elimination method is another example which is a method for solving systems of linear equations that exhibit invariance. It is an algorithm that uses a series of row operations to transform a matrix into a row echelon form, which is invariant under the operations.

The row echelon form represents a simplified version of the original matrix, which can be used to find the solutions to the system of linear equations.

All images/mathematical drawings were created with GeoGebra.

Intersection Sets Definition < Glossary Index > Inverse Definition