Inverse|Definition & Meaning

Operations

An “operation” in mathematics is the calculation of a value utilizing operands and a math operator. The numbers utilized in operation are referred to as operands. 

Different words are applied to the operands based on the type of operation. Operators are symbols that indicate a mathematical operation, such as • + for addition • – for subtraction • x for multiplication •  ÷  for division • = for equal to indicate equality, i.e., that the values on the left and right are equivalent.

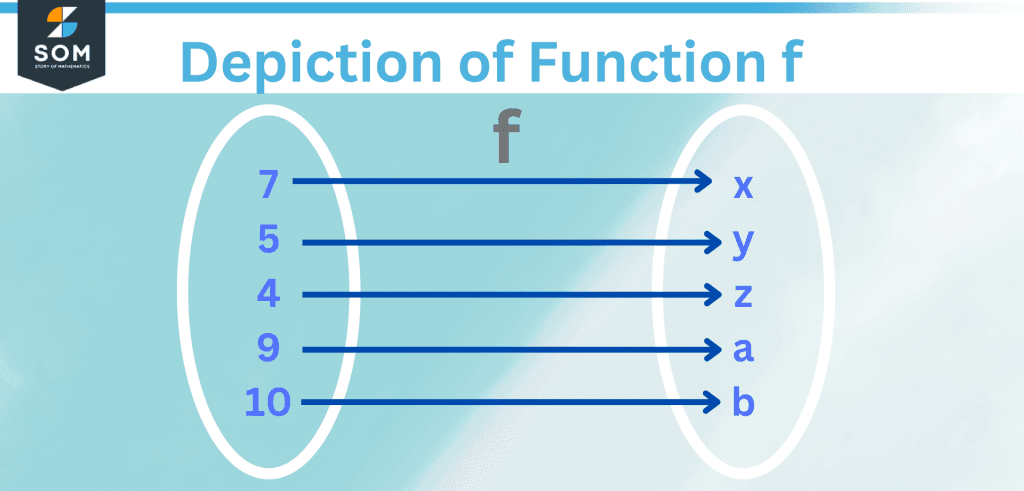
Figure 1 – Depiction of Function f

The inverse of the function in figure 1 essentially reverse the direction of the arrows, so now the output maps to the input! See this in figure 2 below.

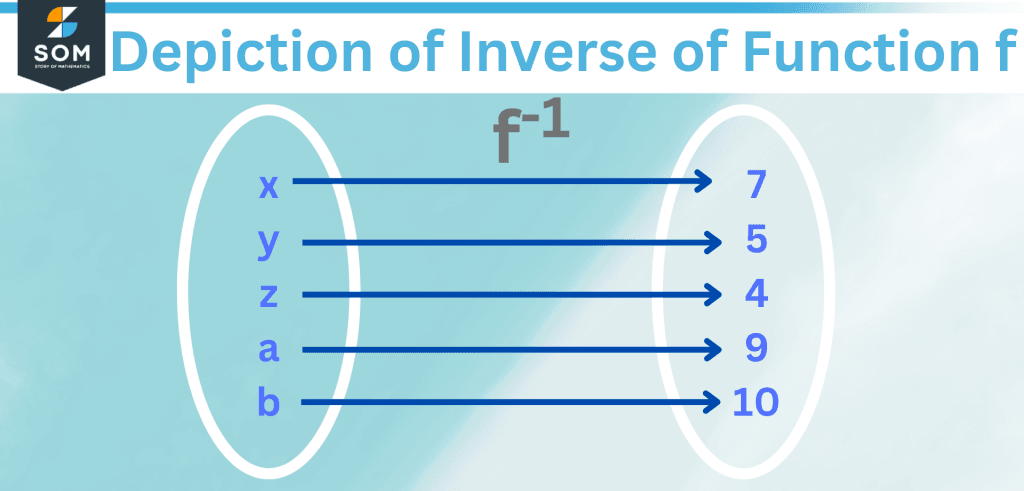
Figure 2 – Depiction of Inverse of Function f

Inverse Operations

Inverse refers to the inverse. Therefore, in mathematics, an inverse operation is the operation that undoes what the prior operation did. Inverse operations refer to the pair of opposing operations.

For instance, if we add five and two pens, we obtain seven pens. Subtract seven pens and two pens, and we are left with five pens. Here, addition and subtraction are performed in reverse order.

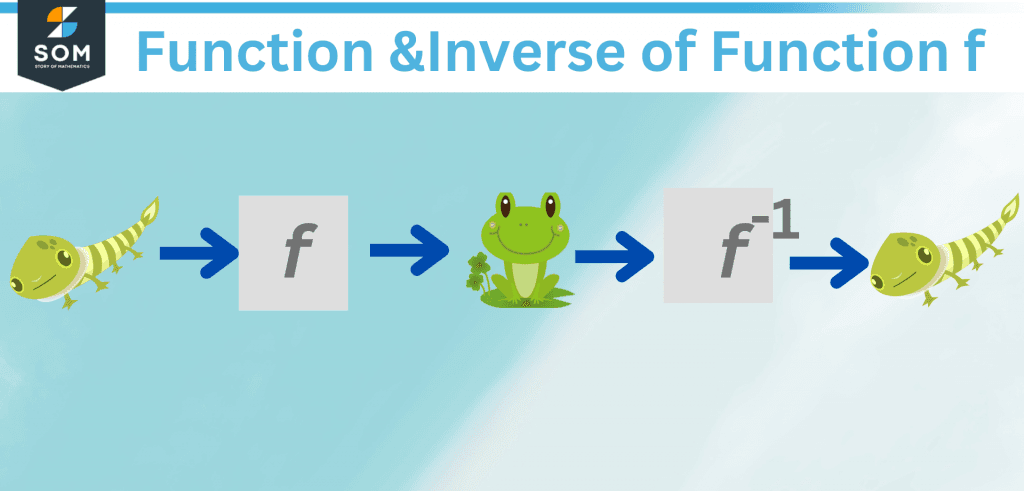
Figure 3 – Tadpole and frog; function and inverse of function

Subtraction and Addition

Subtraction undoes addition, and addition undoes subtraction. We can rearrange the integers in the addition equation and then utilize it to get two distinct subtraction equations.

For instance: 20 + 8 = 28

The two equations created by subtraction are 28 – 8 = 20 and 28 – 20 = 8.

After this, we can even demonstrate that when we take a number, such as 20, then add and subtract the same amount from it, we end up with 20 again. i.e., 20 + 8 – 8 = 20

In a similar manner, we can rearrange the integers in the subtraction equation and create two addition equations. For example: 30 – 14 = 16

The resulting addition equations are 14+16=30 and 16+14=30. When a number is added and then subtracted later, the effect is reversed. 16 – 4 + 4 = 16

Calculating Multiplication and Division

Multiplication and division are inverse operations. Therefore multiplication reverses division, and division reverses multiplication. We can rearrange the integers in the multiplication equation and derive two distinct division expressions. for example: 7 x 4 = 28

The two resulting division equations are 28 ÷ 4 = 7 and 28 ÷ 7 = 4.

Also, the impact is inverted when we multiply a number and then divide it later on. 12×4=48; 48 ÷ 4 = 12

In a similar manner, we can rearrange the values in the division equation and create two multiplication equations. for example 45 ÷ 9 = 5

The resulting multiplication equations are 9 x 5 = 45 and 5 x 9 = 45.

In addition, when we divide a number and then multiply it later, the impact is inverted. 12 ÷ 4 = 3; 3 × 4 = 12

Properties of Reversible Operations

Property of Inverse Additivity

The value that yields 0 when added to the initial number is known as the additive inverse.

If x is the initial number, then its additive inverse is minus of x, or -x, so that: x + (– x) = x – x = 0

For instance, 6+(-6) = 0. Consequently, –6 is the additive inverse of the number 6 and vice versa.

If x is the initial number, its additive inverse is the positive value of x, i.e., x.

Properties of Inverse Multiplication

Multiplicative inverse refers to the value that, when multiplied with the original integer, yields 1.

If x is the initial number, then its multiplicative inverse is the reciprocal of x, i.e., 1x, such that $ \frac {x} {x} $ = 1

For example, 6 multiplied by 16 equals 1. 16 is hence the multiplicative inverse of 6 and vice versa.

If $ \frac {1}{x} $ is the original number, then its multiplicative inverse will be x, which is the reciprocal of $ \frac {1} {x} $ .

The multiplicative inverse of $ \frac {3} {4} $ , for example, is $ \frac {4} {3} $.

The definition of an inverse function or anti-function is a function that may be reversed into another function. If a function “f” transforms x into y, then its inverse will transform y into x. If the function is represented by ‘f’ or ‘F,’ the inverse function is represented by ‘f^-1‘ or ‘F^-1‘. In this situation, an exponent or reciprocal should not be confused with (-1).

In trigonometry, the angle measure for which the sine function yielded a value is found using the inverse sine function Sin$^{(-1)} = sin^-1. For example, since sin(90 degrees) = 1, the inverse gives the angle sin${-1}$(1) = 90 degrees.

A function accepts values, applies specific operations to these values, and produces an output. The inverse function corresponds to the resultant, operates, and returns to the initial function.

The inverse function returns the original value that a function’s result was based on.

The inverse functions of f and g are f(g(x)) = g(f(x)) = x. if we examine functions. A function composed of its inverse retrieves the initial value. for example: f(x) = 2x + 5 = y, g(y) = (y-5)/2 = x is hence the inverse of f (x).

Note that a relationship that results from replacing the independent variable in an equation with the dependent variable; this inverse may or may not be a function. If the inverse of a function is the function itself, it is referred to as the inverse function, indicated by f-1 (x).

Graph of Inverse Function

The graph of the inverse of a function reflects both the function and the inverse of the function over the line y = x. This graph line crosses through the origin and has a slope of 1. It can be written as y = f^-1(x), which equals x = f (y)

This relationship is comparable to y = f(x), which specifies the graph of f, except that the variables x and y are reversed. In order to draw the graph of f^-1, we must switch the placements of the x and y axes.

How Can I Determine the Inverse of a Function?

Typically, an inverse is calculated by exchanging the x and y coordinates. This newly established inverse is a relation but not necessarily a function.

The original function must be a one-to-one function in order to guarantee that its inverse will also be a function. Only when every other element in a function matches the first value is it deemed to be a one-to-one function (values of x and y are used only once).

To ascertain whether a function is a one-to-one function, utilise the horizontal line test. The function is a one-to-one function, and its inverse is also a function. if a horizontal line intersects it in a single place.

Inverse Function Types

There are several types of inverse functions, including the inverses of trigonometric, rational, hyperbolic, and log functions.

Trigonometric Inverse Functions

Because they generate the necessary arc length to reach a particular value, the inverse trigonometric functions are also referred to as “arc functions.” There are six inverse trigonometric functions: arcsine (sin^-1), arccosine (cos^-1), arctangent (tan^-1), arcsecant (sec^-1), arccosecant (cosecant^-1), and arccotangent (cot^-1).

Inverse of Rational Functions

A rational function has the form f(x) = P(x)/Q(x), with Q(x) 0. The procedures below can be used to find the inverse of a rational function. An illustration is provided below to help you better grasp the concept.

• Step 1: Replace f(x) = y with f^-1(x)

• Step 2: Step 1: Swap x and y

• Step 2: Calculate y in terms of x

• Step 3: Find y

• Step 4: Substitute y for f^-1(x) to get the inverse function.

Inverse of Hyperbolic functions

The opposite of a hyperbolic function is a hyperbolic function, similar to inverse trigonometric functions. Existing inverse hyperbolic functions are mostly sinh^-1, cosh^-1, tanh^-1, csch^-1, coth^-1, and sech^-1. Refer to the formula for inverse hyperbolic functions to understand more about these functions in depth.

Inverse Logarithmic and Exponential Functions

The inverse of the exponential functions is the natural log function. Check out the following Example to learn more about the inverse exponential function and the logarithmic function. Develop problem-solving skills by gaining a deeper understanding of how to address comparable problems.

Example of Converse Logic

Determine the inverse function of f(x) = ln (x – 2)

Solution

Replace f(x) with y first.

So, y = ln (x – 2)

Replace the equation with x – 2 = e^y to make it exponential.

Now, solving for x, we have x = 2 + e^y.

Replace x with y, resulting in f^-1(x) = y = 2 + e^y.

All images/mathematical drawings were created with GeoGebra.

Invariant Definition < Glossary Index > Inverse Property Of Addition Definiton