Inverse Property of Addition|Definition & Meaning

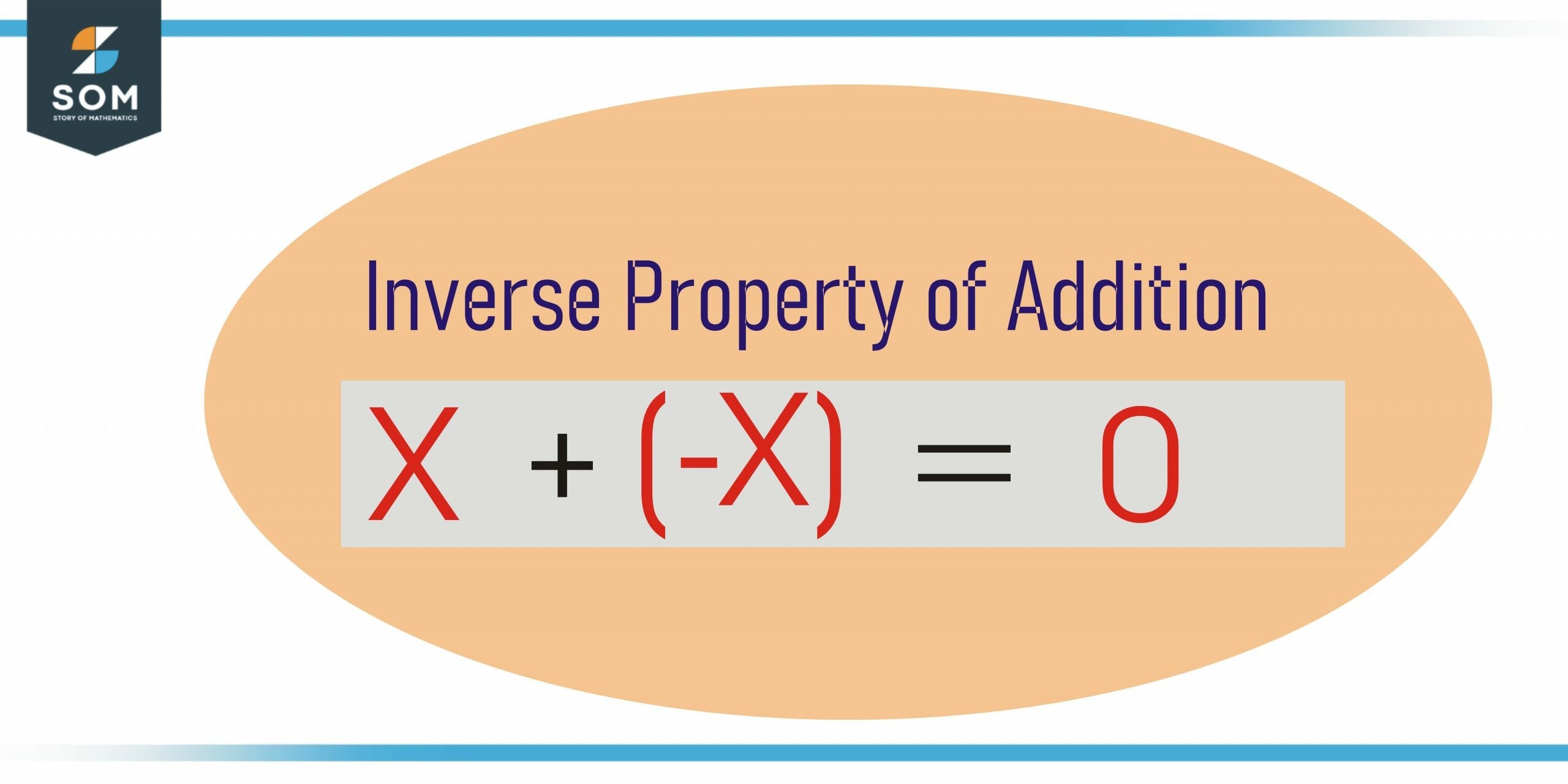
The inverse property of addition can also be elaborated as the property in which a number is added or subtracted to get the result zero.

What Is Inverse?

In mathematics, inverse refers to the opposite effect of numbers. It has many meanings in maths, if the inverse is related to addition or subtraction, it is known as additive inverse. If the inverse is related to multiplication, it is called a multiplicative inverse.

The additive inverse gives a result equal to zero and the multiplicative inverse gives a result equal to one. For the function, the inverse will be to get back the same result that was before the operation of the function. 

The inverse also occurs for sine, cosine, and tangent functions. For the exponents, there are inverses that are represented as logarithms.

Figure 2 – Inverse of any number is the same number with the opposite sign

Inverse operations are the operations that reverse or oppose each other. The most commonly used inverse operations are addition and subtraction.

How the Inverse Property of Addition Is Applied?

In mathematics, there are many properties that are extensively used. The basic purpose to use these properties is to make the calculations simple and easy. The same is the case for the additive property of addition.

This property is applied to make algebraic calculations simple and easy. This property can be used to solve different mathematical equations that might be difficult to solve and just mental maths is applied.

When we are solving an equation, our main aim is to find the value of the unknown variable in the equation so that both the sides of equation become equal. For doing so, the additive property of addition plays a vital role.

Let’s understand this with an example. We are given the following equation:

a + 19.12 = 40.34

We have to solve this equation for a. It can be observed that 19.12 is added to a on one side of the given equation. As the requirement is to isolate the a which means that we want to keep x on one side and all other values on the other side of the equation.

So, we will first subtract 19.12 from both sides.

a + 19.12 – 19.12 = 40.34 -19.12

Here we can see that -19.12 is the additive inverse of 19.12. We know that the inverse property of addition always gives zero results. So, we are left with:

a = 40.34 -19.12

a = 21.22

So, the answer to this problem is 21.22.

Our result can be verified by putting this result into the original equation. When the value of the variable is put in and the equation still satisfies both sides of the equation, our result will be verified.

a + 19.12 = 40.34

21.22 + 19.12 = 40.34

40.34 = 40.34

Hence proving that our answer is correct.

While solving the equations that involve inverse property, we must remember that we can only add or subtract the same number on the two sides of the equation. That way, both sides of the equation remain equal and the additive property of inverse is applied.

Additive Inverse of Real Numbers

The negative of the real number is the additive inverse of that real number. This can be a whole number, a natural number, a decimal number, a fraction, or any other real number. Following are the examples for each of the real numbers.

Natural Number 2. Its additive inverse is -2

Whole Number 4. Inverse is -4

Decimal Number 1.2. Its additive inverse is -1.2

Fraction 3/7. Its additive inverse is -3/7

Additive Inverse of Complex Numbers

A complex number consists of a real number and an imaginary number represented by z. Let’s say a is a real number and i is the imaginary part of a complex number. It is represented as:

z = a + bi

Now, as far as its inverse is concerned, from the basic definition of the inverse property of addition, it is going to be -z. So, the additive inverse of complex numbers can be written as:

-z = -a – bi

Additive Inverse of Fractional Numbers

The concept of the additive inverse of fractional numbers is the same as for real numbers. The additive inverse of fraction x/y is -x/y and the additive inverse of -x/y is x/y.

Difference Between Additive Inverse and Multiplicative Inverse

The additive inverse is for two or more terms separated by an addition or subtraction sign while the multiplicative inverse is for the numbers multiplied with other numbers or variables.

For finding the additive inverse of numbers, the sign of the respective number is changed, and to find the multiplicative inverse, the reciprocal of the number is taken.

The additive inverse is added to the original number to get the result zero while the multiplicative inverse is multiplied by the original number to get the result equal to 1.

The general equation of additive inverse is:

x + (- x) = 0

And the general equation of the multiplicative inverse is:

x * 1/x = 1

Real-Life Solved Example

Jack and Jon are two brothers. They together saved an amount of $500 in a collection jar. They decided to buy a toy. So, they took the amount for purchasing toys from this jar. What is the price of the toy that Jack and Jon purchased if the remaining amount in the jar is $199?

Solution

Let the unknown amount = x

Writing the equation for this problem:

199 + x = 500

To find the value of x, we will apply the additive property of addition.

So, the additive inverse of 199 will be -199. 

Subtracting 199 on both sides:

199 + x – 199 = 500 – 99

x = 301

Figure 3 – The toy Jack and Jon purchased

So, Jack and Jon purchased the toys worth $301.

All the mathematical images are created using GeoGebra.

Inverse Definition < Glossary Index > Inverse Property Of Multiplication Definition