Inverse Property of Multiplication|Definition & Meaning

Figure 1 below shows the multiplicative inverse of 5 into 2.

Figure 1 – Representation of multiplicative inverse of 5 and 2.

Multiplicative Inverse

When a number is multiplied by the original number, the result is 1. That number is said to be the multiplicative reverse of that number. $x^{-1}$, represents the multiplicative inversion of the “x”. In other words, two integers are multiplicative opposites when their product is 1. The divide of 1 by a number yields the second derivative of that number. The number’s reciprocal is another name for it. According to the multiplicative inverse formula, a number’s product with its reciprocal is 1.

Numerous forms of numbers exist, including negative numbers, unit fractions, natural numbers, and fractions of any kind. Let’s learn how each sort of number’s multiplicative inverse formula works.

Natural numbers begin counting with the number 1. A natural number’s multiplicative inverse is 1/x. An example of a natural number is 8. The result of multiplying 8 by 1/8 is 1. As a result, 1/8 is the multiplicative inversion of 8. Likewise, 1/y is y’s multiplicative inverse.

Multiplicative Inverse of Integers

Positive integers can be found to have the same multiplicative inverse as digits (explained above). A negative number’s product and inverse must be 1, just like positive integers. Therefore, the reciprocal of every negative integer is its multiplicative inverse. For instance, the multiplicative inversion of -z is -1/z since (-z) (-1/z) = 1. 

Keep in mind that a negative number’s multiplicative inverse is always negative. Additionally, the negative sign will be attached to the numerator rather than the denominator in the multiplicative inversion of a negative integer.

Multiplicative Inverse of a Fraction

The multiplicative inversion of a fraction a/b is b/a because x/y into y/x = 1 when (x,y $\neq$ 0). For instance, 7/3 is the multiplicative inversion of the number 3/7. The result of multiplying 3/7 by 7/3 is 1 (3/7 x 7/3 = 1). 43/16 is the multiplicative inversion of the ratio 16/43. The result of multiplying 16/43 by 43/16 is 1 (16/43 x 43/16 = 1).

Having one as the numerator makes a fraction a unit fraction. The result of multiplying 1/a by a unit fraction is 1. As a result, an is a unit fraction’s multiplicative inverse, where a = 1/a.

Multiplicative Inverse of a Mixed Fraction

A mixed fraction’s multiplicative inverse can be found by first converting it to an improper fraction and then finding its reciprocal. Find the multiplicative inversion of $4\frac{1}{2}$, for instance.

First, change $4\frac{1}{2}$ to the incorrect fraction 9/2.

Step 2: Calculate 9/2’s reciprocal, or 2/9. The multiplicative inversion of $4\frac{1}{2}$ is thus 9/7.

It’s noteworthy that the correct fraction with a value less than 1 is always the multiplicative inversion of a mixed number.

Figure 2 below shows the multiplicative inverse of a fraction.

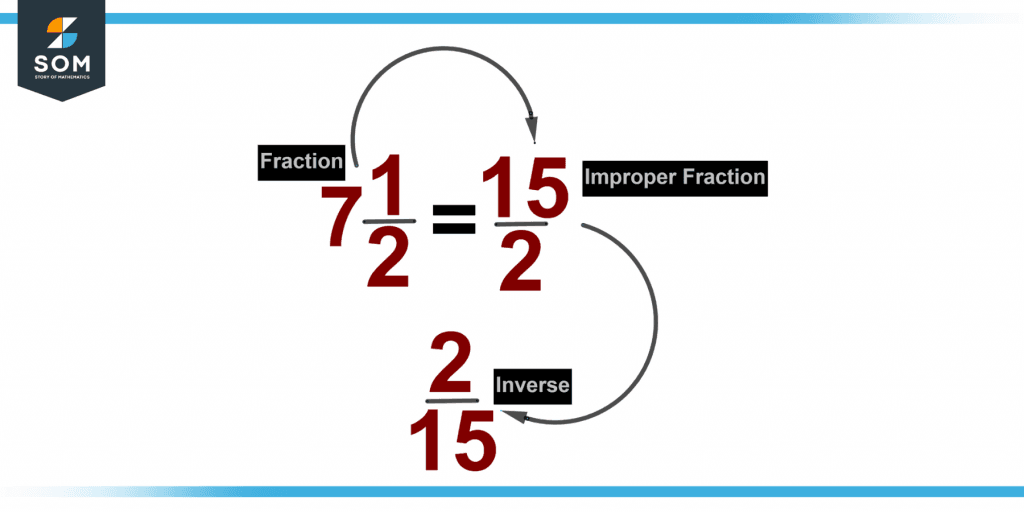
Figure 2 – Multiplicative inverse of fractions.

Multiplicative Inverse of 0

When multiplied by starting amount, the number yields the outcome 1 as the total is referred to as the multiplicative inversion. However, we are known that sum of zero and every other integer has always been zero in the case of zero. Therefore, the multiplicative inversion of 0 is not true.

This may also be understood using the properties of division, which state that sometimes the division of any number by 0 is not stated. The multiplicative inversion of 0 could be expressed as 1/0 even when its value is not given. Thus, it is nonexistent.

Inverse Property of Multiplication

According to the multiplicative inverse property, a number’s product with its reciprocal is always 1. Look at the illustration below, where 1 represents the result and 1/n represents the multiplicative inversion of the integer n.

Figure 3 below shows the multiplicative inverse property.

Figure 3 – Representation of multiplicative inverse property.

Let’s use six bananas as an example. The apples should now be divided into six sections of one each. We need to split them by 6 to create groups of 1 each. A number is multiplied by its multiplicative inversion when it is divided by itself. Therefore, 6 ÷ 6 Equals 6 × 1/6 Equals 1. The multiplicative inversion of 6, in this case, is 1/6.

How To Find Multiplicative Inverse?

The reciprocal of an integer is the multiplicative inversion of that number. The procedures listed below make it relatively simple to determine a number’s multiplicative inverse:

• Step 1: Multiply the supplied number by one.
• Step 2: Format it as a fraction. Say that 1/x is a number’s reciprocal.
• Step 3: Simplify to obtain the solution.

Multiplicative Inverse of Complex Numbers

Complex numbers using the formula Z = x + by, for example, $Z=2+i\sqrt{3}$, where 2 is a real number and $i\sqrt{3}$ is an imaginary number. A complex number Z’s multiplicative inverse is equal to 1/Z.

The procedures shown below can be used to get the multiplicative inversion of a complex number, such as a + ib:

• Step 1 is to write the reciprocal as 1/(a+ib).
• Step 2 The conjugation of (a+ib) is multiplied by this integer and then divided by it.
• Step 3 Apply the following formulas  (x + y)(x – y) = $\mathsf{x^{2}-y^{2}}$ with $\mathsf{i^{2}}$ = -1.
• Step 4 Simplify to the most basic form.

Example of Inverse Property of Multiplication

There are 12 slices on a pizza. The remaining pizza is placed on the table for Jerry’s three friends to divide while he retains 5 pieces at the counter. What percentage of the full pizza does each of his pals receive? Do we use multiplicative inverse in this situation?

Solution

Tom consumed around 40% of the pizza because he only ate five of the twelve slices, and 5/12 = 0.41. The leftover pizza as a fraction would be:

pizza left for Jerry’s friends = 1 – 5/12 = 7/12

Thus, 7/12 of the full pizza must be split amongst 3 pals, represented as 7/12 $\div$ 3, which is the same as 7/12 $\div$ 3/1. To simplify the division, we use the multiplicative inversion of the divisor:

7/12 $\div$ 3/1 = 7/12 $\times$ 1/3

= 7/36

The leftover pizza will be divided into 7/36 portions and given to each of Jerry’s buddies. This means that each of them receives roughly one-fifth (or 20%) of the full pizza as 7/36 = 0.194 $\boldsymbol\approx$ 1/5 = 0.20.

In terms of slices, each friend receives 7/3 = 2.33 slices (two slices and one-third of a slice).

All images are made using GeoGebra.

Inverse Property Of Addition Definition < Glossary Index > Irrational Number Definition