JUMP TO TOPIC
Irregular Polygon|Definition & Meaning
Definition
A polygon is considered irregular if neither its sides nor its angles are of the same length. It differs from a regular polygon, which is a polygon with all sides being the same length and all angles being the same size. Since irregular polygons lack the symmetry and regularity of regular polygons, they can be difficult to work with in geometry.
Overview
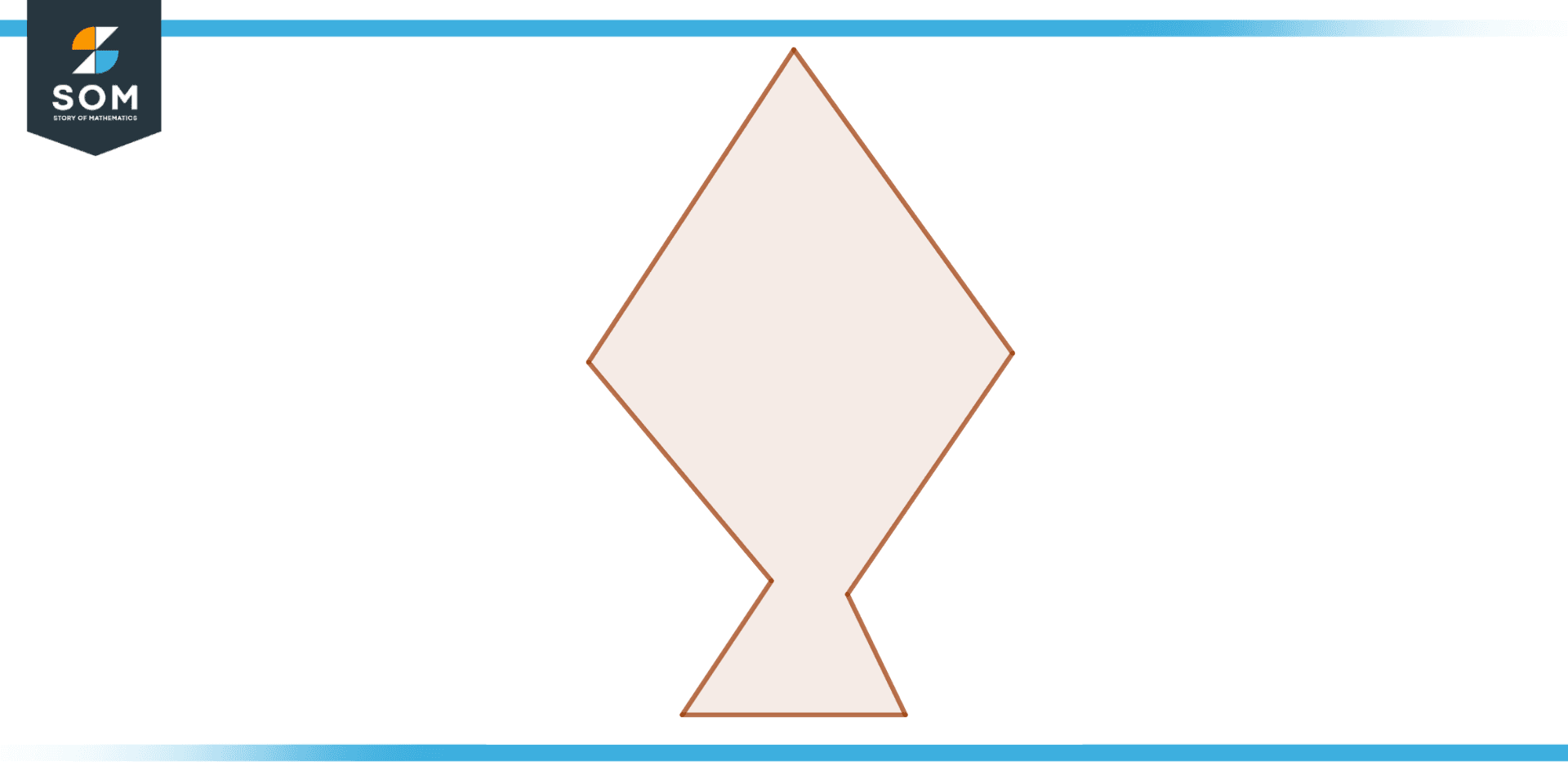
Figure 1 – A simple irregular Polygon
A crucial characteristic of an irregular polygon is that it is not cyclic, which prevents it from being encircled by a circle. This is due to the fact that an irregular polygon’s sides and angles are not equal, making it impossible to distribute them evenly around a focal point. However, irregular polygons can be circumscribed around a circle, which means that the polygon’s perimeter can be enclosed by a circle. The above figure shows an irregular polygon.
Properties of Irregular Polygon
There are several properties that are unique to irregular polygons:
- Irregular polygons cannot be encircled by a circle because, as was already mentioned, they are not cyclic. An irregular polygon cannot be dispersed uniformly around a central point because its sides and angles are not equal.
- Self-Intersecting: Some asymmetric polygons have sides that cross one another to form a shape that is self-intersecting. The bowtie form is an illustration of a polygon that self-intersects.
- Star polygons are irregular polygons that have points or vertices that radiate outward from the center of the pattern, and they can also be categorized as irregular polygons. The pentagram is an illustration of a star polygon that began by cutting the polygon into smaller, more recognizable forms, and calculating the areas of each.
- Non-convex: Some irregular polygons fall into this category if at least one of their angles exceeds 180 degrees. The polygon is “bent” or “curved” inwards in this sense.
- Complex Shapes: Unlike regular polygons, irregular polygons can take on a number of complex shapes, giving them a wider range of possible uses.
- Internal Angles: A formula that takes into account the polygon’s number of sides can be used to compute the sum of the interior angles of an irregular polygon. To get the size of each angle in an irregular polygon, apply this formula.
- Perimeter: An irregular polygon’s perimeter is equal to the sum of all of its sides.
- Area: An irregular polygon’s area can be measured by breaking it up into smaller, more recognizable shapes, then calculating the areas of each of those shapes.
- Lines connecting the non-adjacent vertices of an irregular polygon are known as its diagonals. A formula that considers the number of sides in the polygon can be used to determine the number of diagonals in an irregular polygon.
Regular vs. Irregular Polygon
Regular Polygon
A regular polygon is one that has sides that are the same length and angles that are the same size. In other terms, a regular polygon has congruent sides and angles. Equilateral triangles, squares, pentagons, hexagons, and octagons are some examples of regular polygons.
Irregular Polygon
An irregular polygon is one that has sides that vary in length and angles that vary in size. In other terms, an irregular polygon does not have congruent sides and angles. Scalene triangles, rectangles, and heptagons are a few examples of irregular polygons.
Difference
By examining their symmetry, regular and irregular polygons can be distinguished from one another. A regular polygon is symmetrical, which means that each half would be a mirror image of the other if a line of symmetry were drawn through its center. On the other hand, an irregular polygon lacks this symmetry.
Types of Irregular Polygons
Scalene Triangle
An irregular polygon, more precisely a triangle, with no sides of equal length is called a scalene triangle. It doesn’t have equal-length sides, so it doesn’t have equal-sized angles either. Inferred from the fact that a scalene triangle lacks equal-length sides and angles, it follows that a scalene triangle is an irregular polygon. The irregular polygon is shown in the below figure.
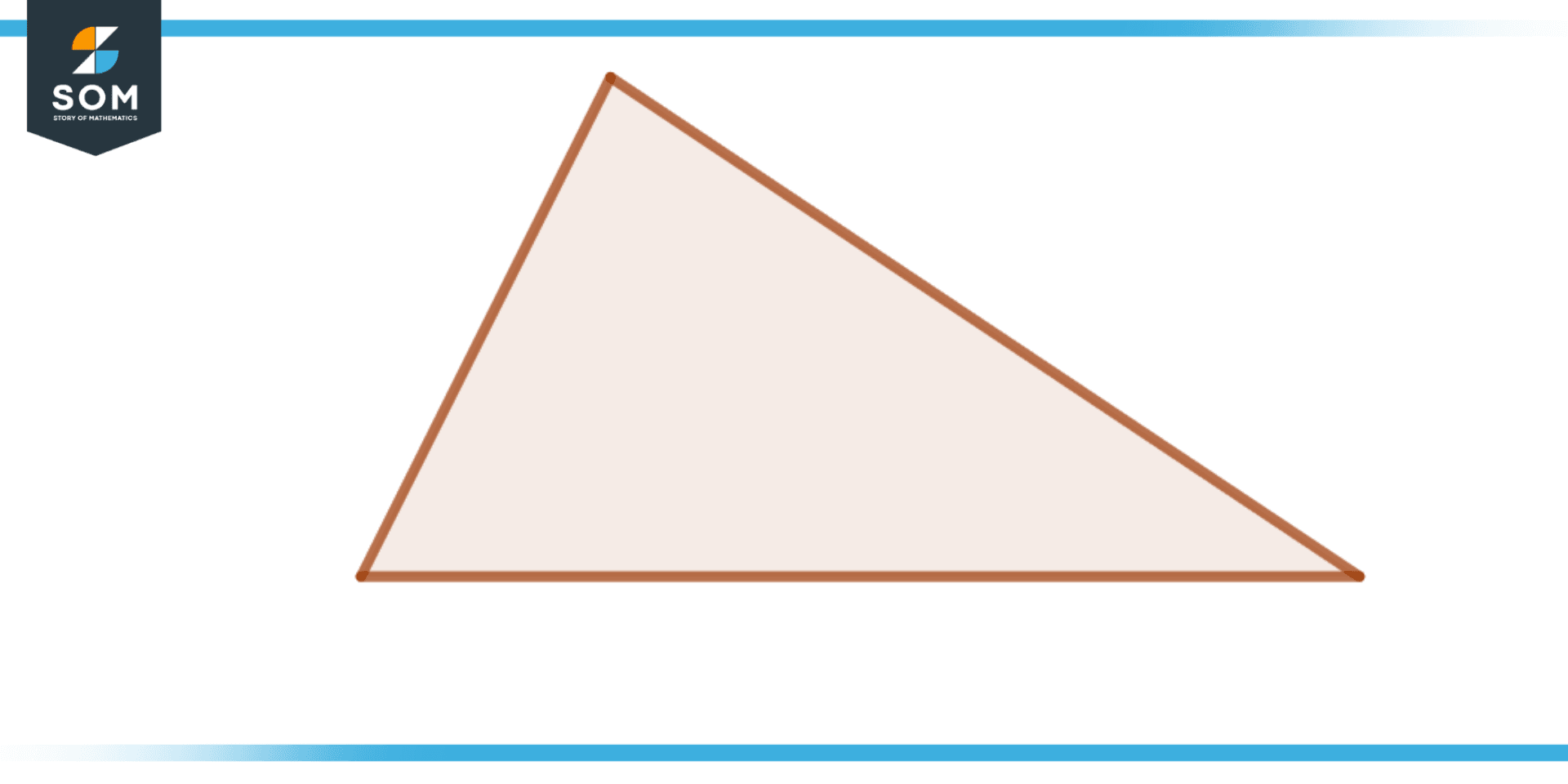
Figure 2 – Scalene Triangle an irregular Polygon
Depending on how big the angles are, a scalene triangle can be acute, right, or obtuse. All of the angles in a scalene triangle are fewer than 90 degrees in an acute triangle, 90 degrees in a right scalene triangle, and greater than 90 degrees but less than 180 degrees in an obtuse scalene triangle.
Right Angle Triangle
A right triangle is a particular kind of irregular polygon that has one angle that is exactly 90 degrees. The right angle is the name for this angle. It is regarded as an irregular polygon because one of its angles isn’t the same as the rest. The irregular polygon is shown in the below figure.
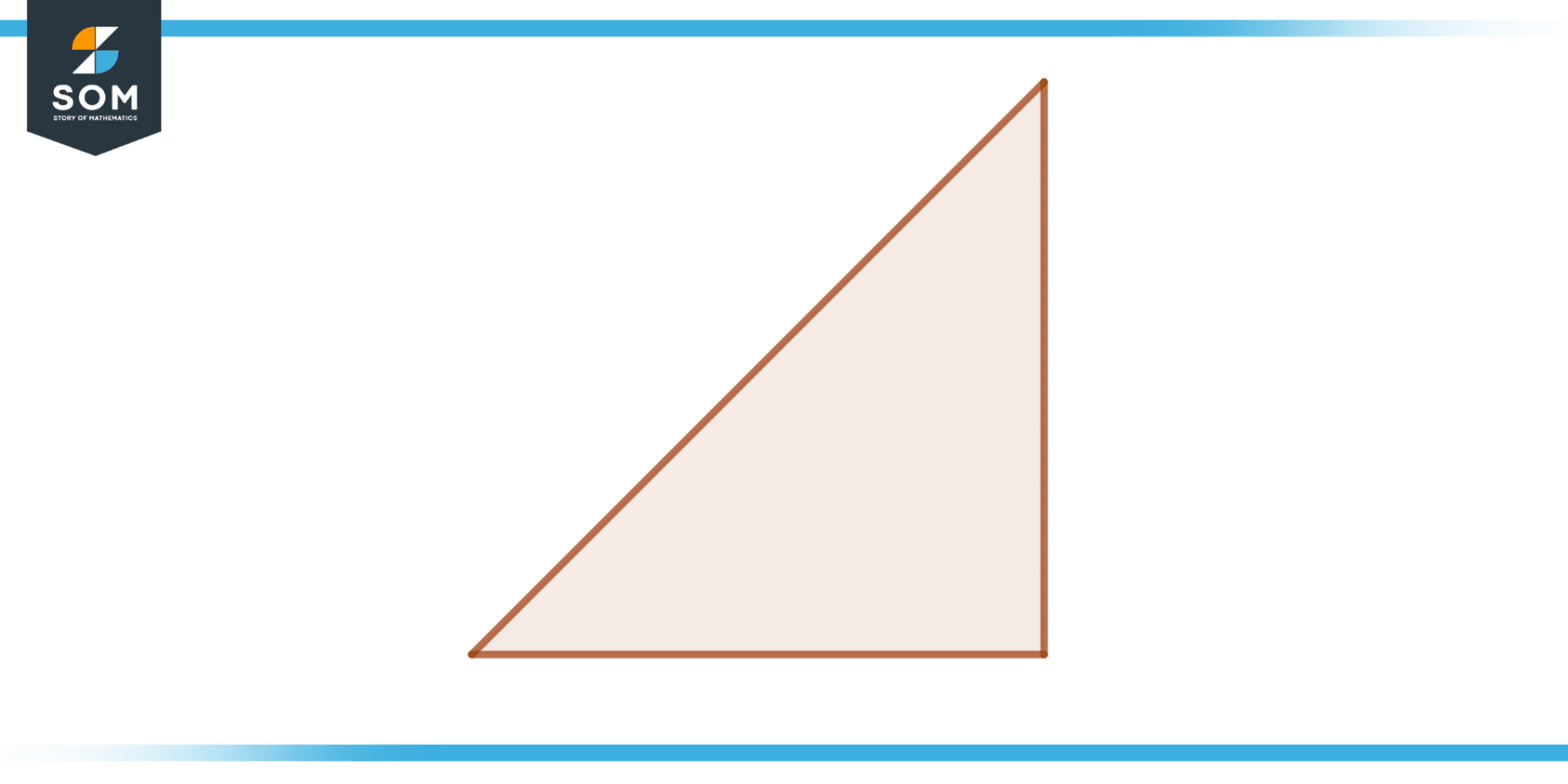
Figure 3 – Right Angled Triangle is an irregular polygon.
A right triangle has two sides unequal in length, with one side being longer than the other, and one right angle. The triangle’s two shorter sides are referred to as the triangle’s legs, while its longer side is known as the hypotenuse. The legs are the two sides that are next to the right angle, and the hypotenuse is the side that is opposite the right angle.
Isosceles Triangle
An isosceles triangle is a particular kind of triangle in which the lengths of the two sides are equal. Its uneven shape is due to the fact that not all of its sides are the same length.
The legs and base of an isosceles triangle are its two equally long sides. The third side is referred to as the hypotenuse. The vertex is the intersection of the two legs, and the angle between them is referred to as the vertex angle. The irregular polygon is shown in the below figure.
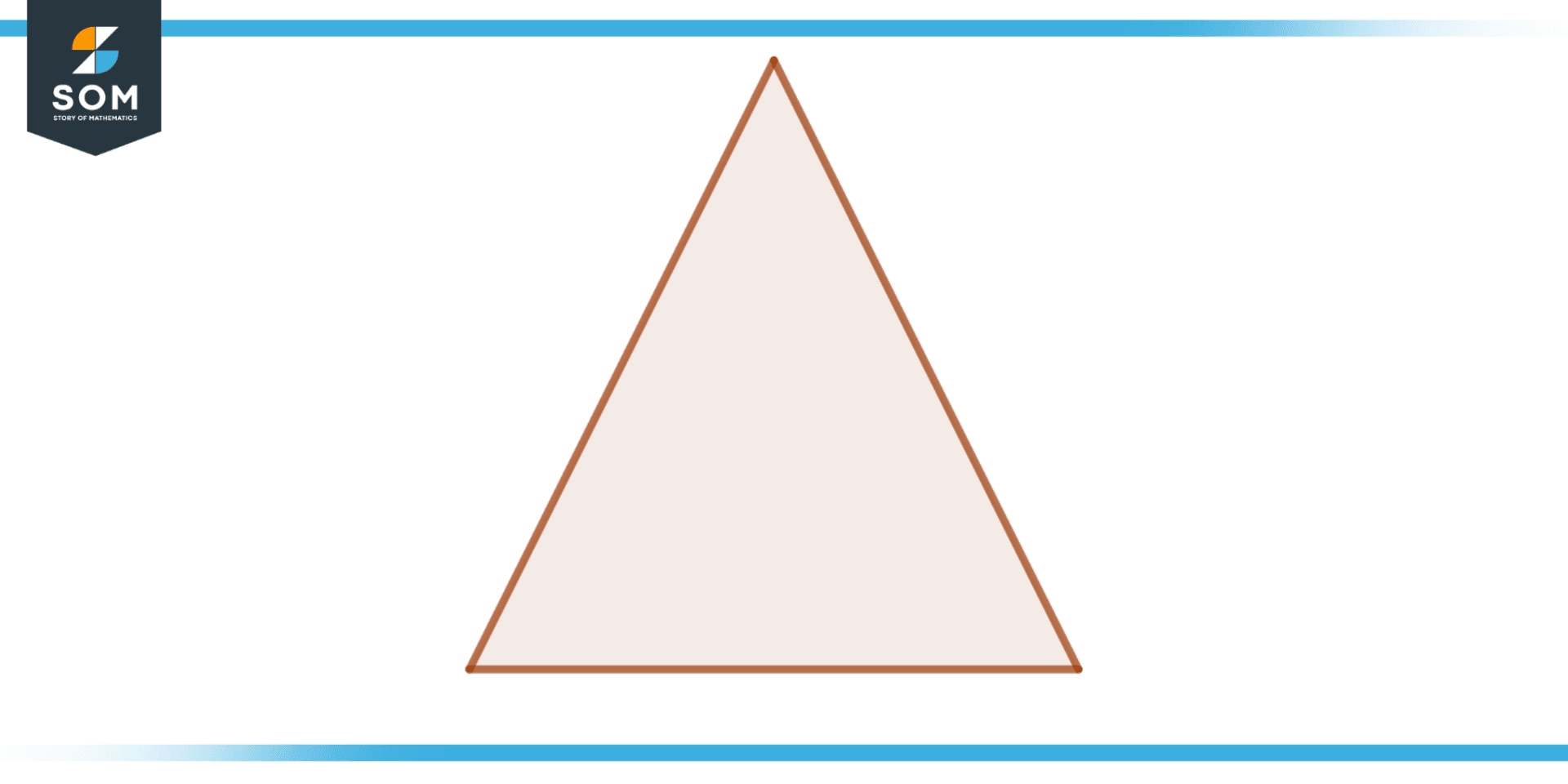
Figure 4 – Isosceles Triangle is an irregular polygon.
Depending on how long the legs are in relation to how long the base is, isosceles triangles can have two acute angles or two obtuse angles. The triangle has two acute angles if the legs are shorter than the base. If the legs are longer than the base, the triangle will have two obtuse angles.
Rectangle
Four-sided polygons with opposite sides that are parallel and equal in length make up rectangles. Its uneven shape is due to the fact that not all of its sides are the same length.
Figure 5 – Rectangle an irregular polygon.
The parallel, equal-length sides of a rectangle are referred to as the length and width. Usually, the length is more than the width. The width is represented by the two shorter sides and the length by the two longer sides. A rectangle’s area is equal to the product of its length and width, and its perimeter refers to the distance around its outside. The irregular polygon is shown in the above figure.
Example Involving Irregular Polygon Calculations
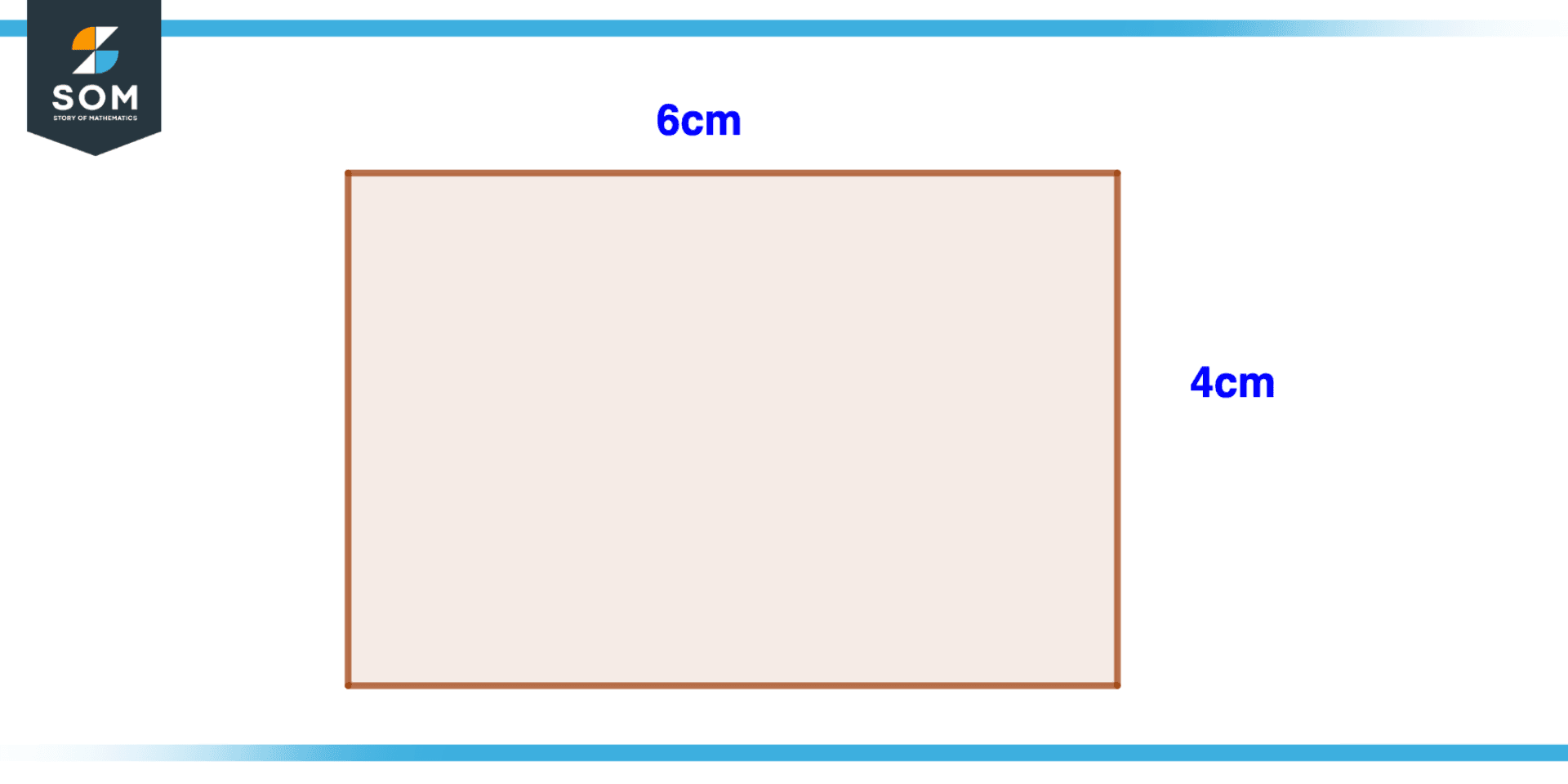
Figure 6 – Area of Irregular Polygon example
Consider an irregular polygon shown in the figure. Find the area of this polygon.
Solution
As this is a rectangle so we can find its area by the formula of the area of a rectangle.
Area of rectangle = Length x Width
Area of rectangle = 6 x 4
Area of rectangle = 12 sq. units
All mathematical drawings and images were created with GeoGebra.
