Isometric|Definition & Meaning

However, scaling is not isometric; the distance between its points will alter after scaling the triangle.

Figure 1 below shows an isometric drawing of a cube.

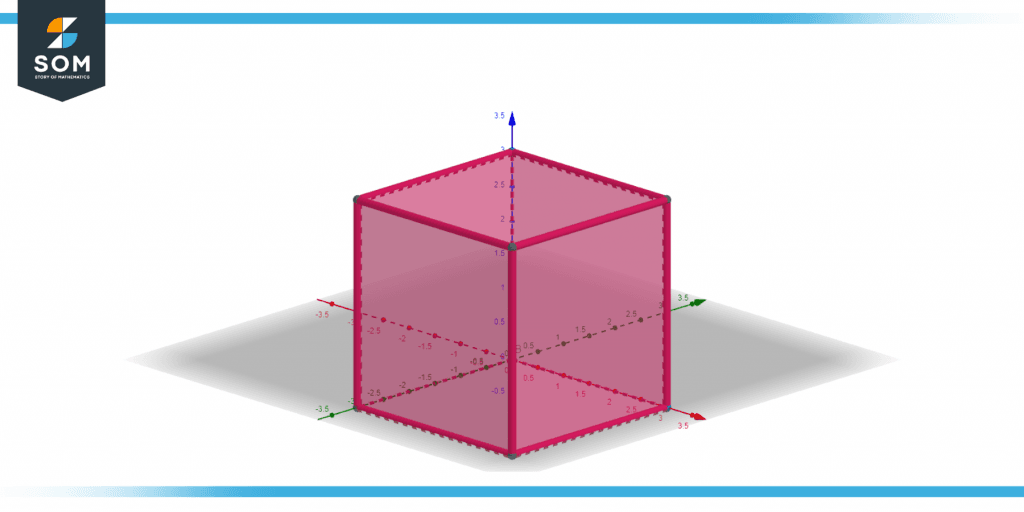
Figure 1 – Isometry of a cube.

Isometry 

Isometry is a transition that maps elements with the same or some other topological spaces such that the spacing between the image objects in the new topological spaces is equally distant between both the components in the original topological spaces, given topological spaces (loosely, an initialized and a scheme for allocating distances among elements of the set). 

Different geometric figures are said to be congruent in a two-dimensional and three-dimensional Ellipsoid if an isometry connects them. This isometry can be either a stiff motion (translate or rotation) or a composite of rigid mobility and a reflection. 

Congruency

Congruent triangles are if the three sides and the three columns of both angles are identical in any triangle orientation.

A distance-preserving transformation across metric spaces known as an isometry (also known as congruence or congruent transformation) is often believed to be bijective. In structures where one area is encased inside another, isometries are frequently employed. For instance, an isometry through M into M’ a split set of the universe of Cauchy sequence on M, is required to complete a metric space M. 

Figure 2 shows the congruence of 2 triangles.

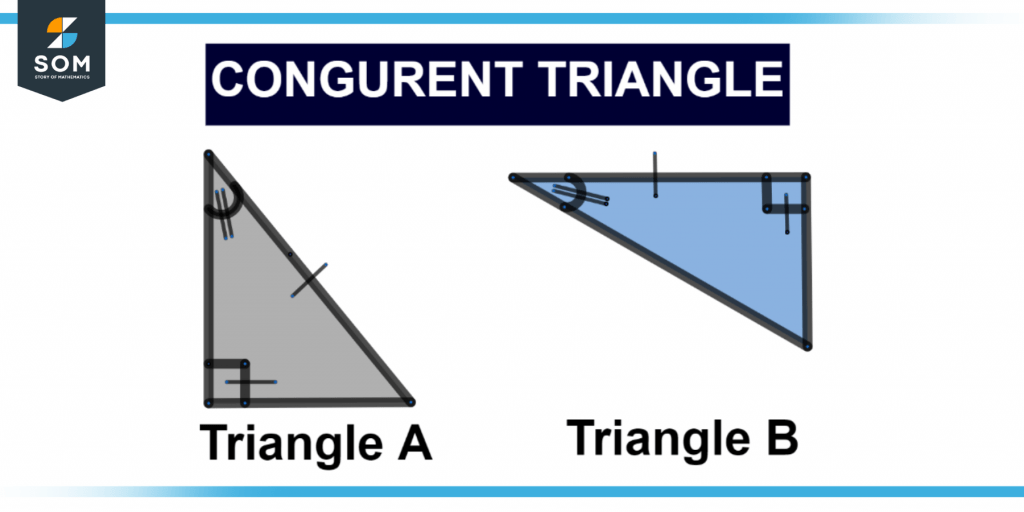
Figure 2 – Congruent triangles.

As a result, the original space M, typically referred to as this subspace, is an isometric contraction isomorphic to a hyperspace of a whole metric space. Furthermore, every full metric field is isometric contraction isomorphic to the close subset of certain Banach space, according to other embedding methods, and every normed vector space is isometric contraction invariant to a close subset of any normed space.

An isometric surjective nonlinear operator on the Hilbert space is a unitary operator.

Global Isometry

Global isometry or Bijective isometry refers to congruence mapping or isometric isomorphism. A global isometry has an inverse function, just like any other bijection. Global isometric is indeed a global isometry’s inverse.

If there is indeed a bijective isometry between two metric spaces, X and Y, then the two metric spaces are said to be isometric. The isometry group, which refers to the collection of isometry bijective from the topological spaces to itself, is formed concerning function composition.

The weaker concept of route isometry or circle-wise isometry is also present.

A route isometry and isometry arc wise is a mapping that keeps curve lengths intact; this type of map is not always an isometry inside the sense of maintaining distance, nor does it have to be bijective or even injective.

Types of Isometry

Isometry comes in three types: rotation, reflection, and translation. Each of these isometry kinds calls for a particular adjustment to be performed to a picture or object. The initial picture or object is referred to as a pre-image. The final picture or object that results from applying the various isometries on the pre-image is known as the post-image.

Rigid Transformation in isometry: Rigid transformation is defined as one is only interested in changes to an item or image’s location, direction, and orientation, not its shape or appearance. 

A pre-image is projected on the plane in coordinate geometry. 

A post-image would be created following a transformation. 

The similarity between the two photographs should be highlighted. Geometric congruency refers to the shape and size of two objects having the same angles and points on both the pre-and post-images.

Translation

A translation is an isometry in which the pre-image changes due to sliding along a plane. It could include moving horizontally to the right or left. Vertical movement up or down is another possibility. 

Any location that alterations can describe in the plane’s lateral and vertical position is possible for the pre-image to go to. With the pre-image with post-image matching in size and form, this is seen visually as a “slide.” The photos are also in the same orientation. It resembles moving two similar figures up, down, and to the left or right.

Reflection

The reflection is described as a change inside an image caused by a flip or folding operation over a line. The mirror line or even the lines of reflection are other names for this line. On the opposite side of this line, the reflection of the picture on one side is visible.

Another approach to thinking about a reflection motion is to see the pre-image as the reflection of the post-image and the lines as the reflection between the two pictures. On a graphic level, the pre-image and post-image locations’ distances from the mirror lines are the same. 

Figure 3 below shows the reflection isometry.

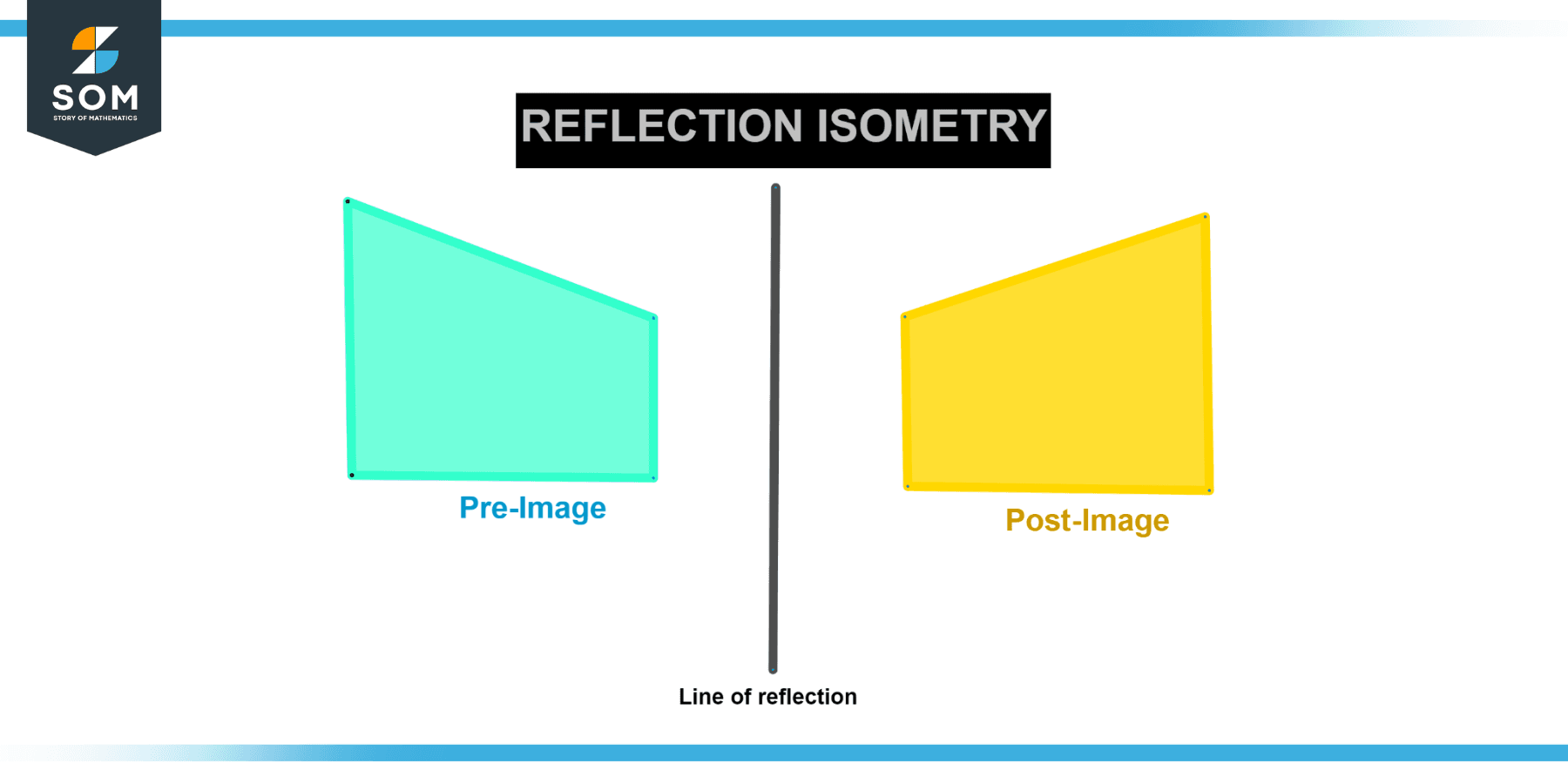
Figure 3 – Representation of reflection isometry.

Rotation

Rotation secures an item or picture on a pivot that serves as a guideline and moves it at a precise angle. This pivot is referred to as a rotor center. This implies that all the elements in the image are kept at constant ranges from the rotor center. The clockwise or counter-clockwise direction of a turn is also specified. If angle measurements are supplied, rotate either counter-clockwise to represent negative or positive angles accordingly.

Example of Isometric Figures

What isometry connects Figures 1 and 3? Using the concept above, find the type of isometry in the triangles below.

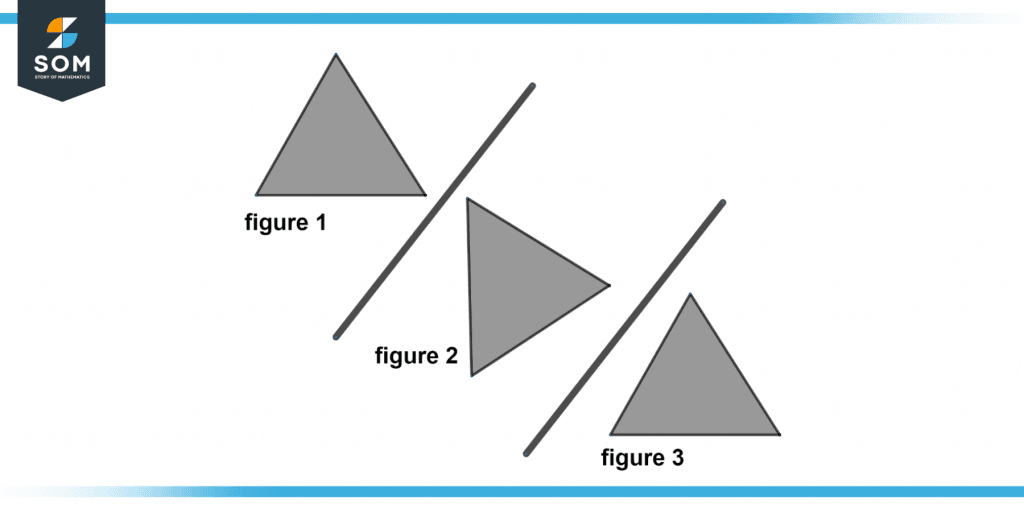
Figure 4 – Isometry between triangles.

Solution

Step 1: Transformation called an isometry occurs when the actual figure and its image are congruent.

Step 2: The figure is turned over a line by a reflection. The previous figure is mirrored in the new figure.

Step 3: Figures 2 and 3 reflect Figures 1 and 2, respectively.

Step 4: A translation is made up of two reflections that are parallel to one another.

Step 5: Since Fig. 1 and Fig. 3 are related by a translation, this isometry.

All images are made using GeoGebra.

Irregular Polygon Definition < Glossary Index > Iteration Definition