Iteration|Definition & Meaning

By beginning with an initial estimate and then continuously improving until it is correct to within a specified tolerance, you could use iteration to discover the cube root of a number. Iteration can also be used to produce number sequences, solve equation systems, and carry out other kinds of calculations. 

Figure 1 – Iteration Disc

Iteration is the process of repeatedly doing a task. It is a typical method for locating approximations of issues that cannot be addressed precisely.

Iteration Formula

Iteration is a numerical technique for approximating an equation’s root (solution).                                                        

y = f(x), where f(x) = 0

For instance, the sum of squares of an integer can be determined iteratively by beginning with an initial estimate and then repeatedly refining the estimate until it is sufficiently correct.

The technique of employing a recursive formula to generate a series of integers is another example of iteration. For instance, the next number in the Fibonacci numbers is created by adding the two numbers before it in the sequence.

Illustration

Numerous mathematical disciplines, such as numerical methods, computer science, and engineering, require iteration. It is a crucial tool for figuring out approximations to problems that don’t have exact answers or for addressing issues that necessitate a high level of accuracy.

The repetition of a procedure or function is known as an iteration. It is a key idea in many branches of mathematics, such as programs, complex systems, and iterative approaches to equation solving.

Mathematicians use the idea of iteration to solve problems, create sequences, and comprehend complicated systems. It is applied in several situations.

Additionally, numerical techniques for resolving differential equations employ iteration. Differential equations are used to simulate a variety of events in the social and natural sciences. They are expressions that explain how even a function changes in time.

Equations can be challenging to solve, particularly when they are complex, or the exact solution is unknown. In these situations, by segmenting the problem into smaller sections and resolving each one separately, we can use an iterative to approach the solution. Numerical integration is the process in question.

Detailed Description

Iteration is a mathematical technique that has a variety of applications. Finding the limit of a sequence is one frequent application of iteration. The iterative approximation is a technique that can be used to do this. In this method, a first guess is made regarding the limit’s value, and this guess is subsequently improved by repeatedly using a function on the prior guess.

The process of iterating is employed in mathematics to resolve equations. Iterative techniques can be used to solve a variety of equations, especially ones that can’t be solved using conventional techniques. These techniques entail formulating an estimation for the solution and repeatedly using a function to improve it until it is as accurate as desired.

Figure 2- Iteration Steps

Numerous applications of mathematics, including numerical analysis and optimization, also require iteration. Iterative approaches are employed in various domains to tackle issues of determining a function’s minimum or maximum or approximating the solution to differential equations.

Iteration is a useful and significant mathematical tool that is applied to a variety of issues across many different domains.

The process of iteration can also be employed to identify trends in data or forecast future values. Iteration can be used, for instance, by a mathematical model to forecast the long-term value of a stock market based on historical data.

Overall, iteration is a useful mathematical technique that enables us to tackle challenging issues and make predictions about our environment. It is employed across a variety of disciplines.

Use Iteration To Solve Equations

Iteration is a technique used to find approximate solutions to progressively difficult equations. Iteration refers to performing a process repeatedly. Start with an initial value and enter it into the iteration formula to get a new value. Then, use the new value for the next replacement, and so on, to resolve an equation using iteration.

Let’s say we wish to determine the value of a function f(x) (f(f(f(x))). The function f would have to be used three times for this. Another option is to repeat a procedure, such as calculating the square root of a number. For instance, we could begin with a first guess, such as x = 2, to get the square root of 20.

Then, by averaging with the amount we are attempting to discover the square root of (20/2 = 10 in this case), we might continue the process of refining our hypothesis.

The updated estimate would be (2+ 20)/2 = 10. Until we achieve the necessary degree of accuracy, we might carry on with this method, taking every new guess as that of the inputs for the subsequent iteration.

In mathematics, iteration is a potent technique that can be used to address a variety of issues.

Iteration Process

The fact that the outcome of one iteration of the method serves as the input for the subsequent iteration is a crucial component of the iteration process.

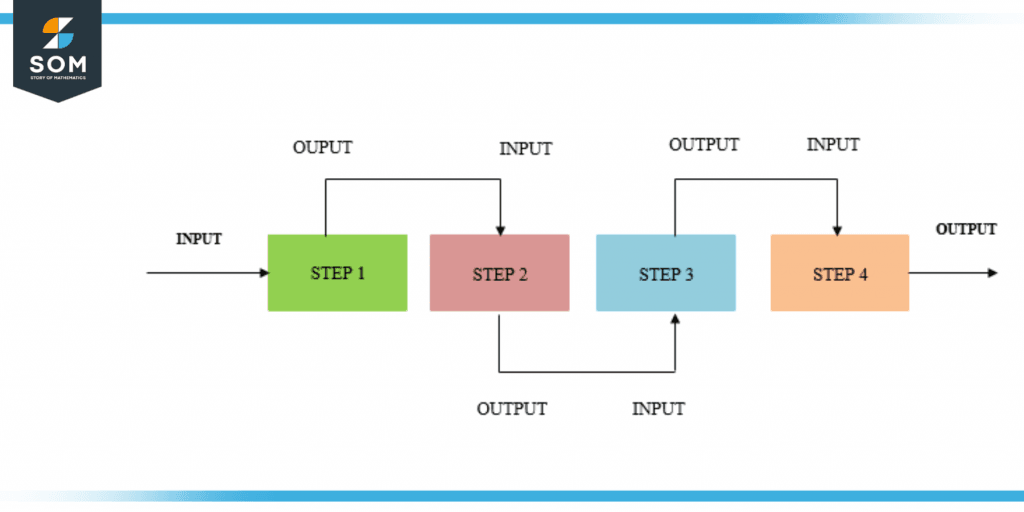
Figure 3 – Visual Representation of Iteration Process

Examples of Calculations With Iterations

Example 1

If x₀=5, by using the iteration formula x_n+1=4+ x_n to find the value of x₄.

Solution

x₀ = 5

x₁ =4+ x₀ = 4+5 = 9

x₂= 4+ x₁= 4+9 = 13

x₃ = 4+ x₂=4+13 = 17

x₄= 4+ x₃=4+17 =21

x₄ =21

So there are four iterations, and it can be clearly seen that this is the forward process. The previous value is fed forward to the next value to get to the final answer.

Example 2

If x₀=2, by using the iteration formula x_n+1= 5 x_n– 3 to find the value of x₃.

Solution

x₀ = 2

x₁=5 x₀-3 = 5(2) -3 = 7

x₂ = 5 x₁-3 = 5(7) -3 = 32

x₃ = 5 x₂-3 =5(32) -3 = 157

x₃=157

All the figures above are created on GeoGebra.

Isometric Definition < Glossary Index > Joule Definition