JUMP TO TOPIC
Joule|Definition & Meaning
Definition
A joule is defined as the energy released when a force of 1 Newton causes an object to displace by 1 meter. It is denoted by the letter J.
An important quantity that involves joules is power, which is the rate of energy consumption.
Power of 1 watt means that 1 joule of energy is consumed in one second.
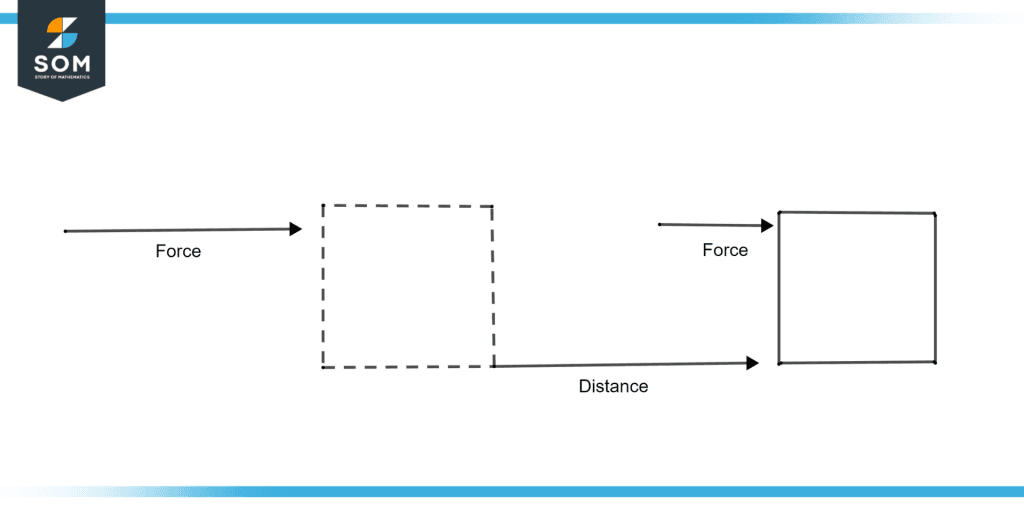
Figure 1: Work done
Figure 1 illustrates the work done to move the box to a distance when force is applied to it.
Jules is named after James Prescott Jules. Like other SI units named after a person, the symbol begins with a capital letter (J). When written in full, it follows the capitalization rules of common nouns. That is, “Joule” is capitalized at the beginning of sentences and titles and lowercase otherwise.
The “Giorgi system” was accepted in 1935 by the International Electrotechnical Commission, the organization that succeeded the International Electrical Congress. This system assumed a specified value for the magnetic constant, which entailed a redefinition of the Joule. The International Committee for Weights and Measures authorized the Giorgi system in 1946.
The joule was now defined as the unit of work done by one unit of force (at the time not yet designated newton) across a distance of one meter rather than based on the electromagnetic unit.
The joule was specifically designed to be used as the unit of energy in both mechanical and electromagnetic settings. The joule was added as a preferred unit of heat in the context of calorimetry when the definition was ratified at the ninth General Conference on Weights and Measures in 1948, formally deprecating the usage of the calorie.
The labor needed to carry a one-coulomb electric charge via a one-volt electrical potential difference, or one-coulomb-volt (CV), is another way to define a joule. The definition of the volt may be found in this connection.
One watt-second (Ws) is the labor necessary to create one watt of electricity for one second (compared to a kilowatt-hour, which is 3.6 megajoules). The definition of the watt may be found in this connection.
Practical Examples of Joule
Following are the practical examples of a joule:
- The amount of power needed to run a 1 W gadget for one second.
- The amount of power needed to move a 1 kg mass 1 meter per square second in one direction.
- The kinetic energy of a mass of 1 kg moving at 1.41 meters per second or a mass of 2 kg moving at 1 meter per second.
- Considering that a medium-sized tomato weighs 101.97 grams, the energy needed to raise it up 1 meter (3 ft 3 in) (3.597 oz).
- The amount of heat needed to bring the temperature of 0.239 g of water from 32 °F to 33.8 °F, or from 0 °C to 1 °C.
- Every 1/60 second, a person at rest typically releases heat (17 meters per second).
- The kinetic energy of a 50-kilogram person moving at a speed of 0.22 meters per second (0.72 kilometers per hour).
- The kinetic energy of a tennis ball weighing 56 g traveling at a speed of 6 m/s (22 kilometers per hour).
- The amount of dietary energy (kcal) in a sugar crystal is little more than half (0.102 milligrams per crystal).
Conversion of Joule to SI Multiples of Joule
Following are the examples of Joule to SI multiples of Joule
Zepto Joule
One electron volt is approximately 160 zeptojoules.
The Landauer limit provides the smallest amount of energy – around 2.75 ZJ – required to modify a little at about room temperature.
Nano Joule
A flying mosquito has a kinetic energy of roughly 160 nanojoules.
Micro Joule
The Large Hadron Collider (LHC) generates microjoule order (7 TeV) collisions for each particle.
Kilo Joule
Most nations use kilojoules to indicate energy on food labels (kJ). In broad daylight, the Earth gets around 1.4 kilojoules of solar energy per second.
Mega Joule
The megajoule roughly corresponds to the kinetic energy of a vehicle weighing one megagram (tonne) and traveling at 161 km/h (100 mph). Approximately 4.2 MJ of energy is needed to heat 10 L of liquid water at constant pressure from 0 °C (32 °F) to 100 °C (212 °F). 3.6 megajoules make up one kilowatt-hour of energy.
Work Done
We say that work is done when a force applied to some object causes it to move in the direction of the force. If the distance covered by an object is zero, then the work done will also be zero. Work done is defined by an equation as follows
Work done = Force $\times$ distance $\times$ cos$\theta$
Where $\theta$ is the angle between the applied force and direction of movement.
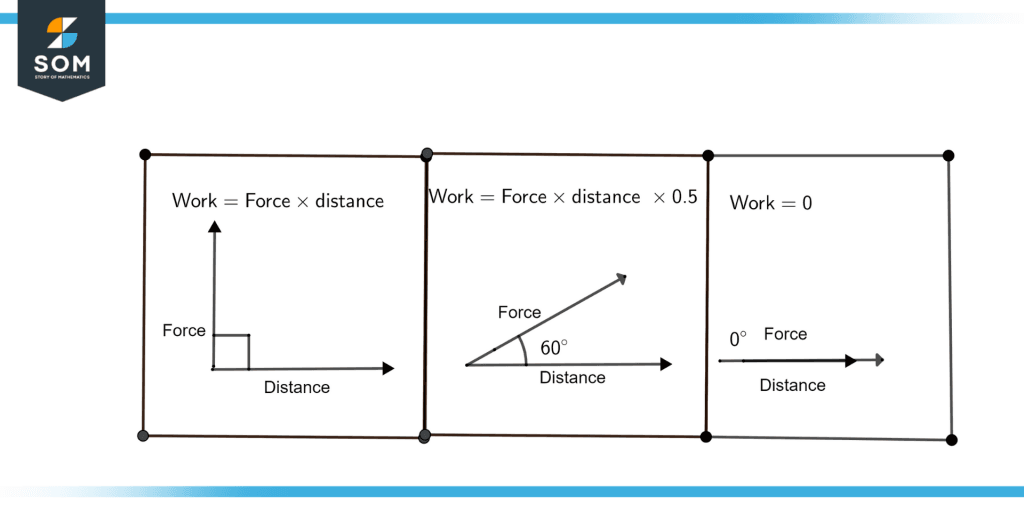
Figure 2: Relationship of angle between force and distance
Figure. 2 illustrates the relationship of the angles between force and distance for work done.
Energy
Energy is defined as the ability of something to do work. According to energy conservation, energy cannot be created or destroyed. The joule (J) is a basic unit of energy.
Efficiency
Efficiency is the percentage of energy that is used that is beneficial.
Efficiency = $\dfrac{\textsf{Useful Energy}}{\textsf{Total Energy}} \times$ 100
Some Examples of Joule
Example 1
Find the total work done illustrated in figure 3 when a force of 200 newtons is applied on the box, and the box covers the distance of 10 meters with an $\theta$=40°.
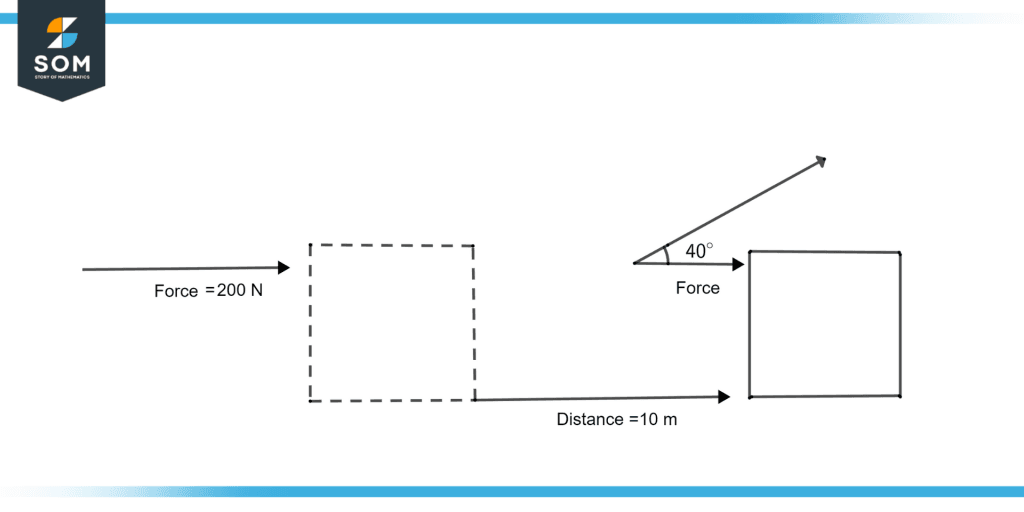
Figure 3: Total amount of Work done
Solution
We know the formula for work done is:
Work done = Force $\times$ distance $\times$ cos$\theta$
Work done = 200 N $\times$ 10 $\times$ cos(40)
Work done = 200 N $\times$ 10 $\times$ 0.766
Work done = 1532 Nm
Work done = 1532 J
Example 2
Find the efficiency of an engine when 50 megajoules of energy a gasoline engine uses, only 30 megajoules goes to driving it forward.
Solution
As we know, the formula of efficiency also from the given data the useful energy is 30 megajoules and total energy is 50 megajoules:
Efficiency = $\mathsf{\dfrac{30 \textsf{ MJ}}{50 \textsf{ MJ}}} \times$ 100
Efficiency = 0.6 $\times$ 100
Efficiency = 60%
The efficiency of an engine is 60 percent.
Images were created using GeoGebra.
