JUMP TO TOPIC
Kilogram|Definition & Meaning
Definition
The kilogram is the unit of mass defined by the international system of units. It is denoted by kg.
The kilogram has been defined in relation to the second and the meter, both of which are based on fundamental physical constants. This enables a metrology lab with the appropriate equipment to calibrate a mass measuring device, such as a Kibble balance, to calculate a precise kilogram mass.
One liter of water’s mass was the initial definition of the kilogram in 1795. To within 30 parts per million, the modern definition of a kilogram matches the original. In 1795, the French spelling was chosen in Great Britain, while the spelling kilogram was adopted in the United States.
Both spellings are used in the United Kingdom. However, “kilogram” has become significantly more prevalent. The use of either spelling is not prohibited by UK legislation, which governs the units to be used when trading in weights or measures. Figure 1 illustrates different weights.

Figure 1 – Weights
The French word kilo, a contraction of the kilogram, was introduced into the English language in the 19th century and is now used to denote both a kilogram and a kilometer.
For example, according to The Economist, the kilo is a good substitute, but the Government of Canada’s Premium Plus system prohibits its use “SI (International System of Units) in scientific and technical writing” and Russ Rowlett’s “ A dictionary of units of measurement called ‘common informal names’.
The term “kilo” could be used as an alternative to the word “kilogram” when the metric system was given legal standing by the US Congress in 1866, but that status was abolished in 1990.
Kilogram As a Base Unit Due to Electromagnetism
The kilograms rather than the grams were finally chosen as the foundation unit of mass in the SI, partly due to units for electromagnetism. The pertinent discussion and decision-making process began around the 1850s and was effectively finished in 1946.
“Practical units” for electrical and magnetic quantities, such as amperes and volts, were established in everyday life at the end of the 19th century. Unfortunately, they did not coincide with the centimeter and gram, the primary basic units for measuring length and mass at the time.
In particular, the watt, a purely mechanical unit of power, is produced by multiplying the ampere and volt. It was discovered that under a system where the meter and the kilogram served as the basic units of length and mass, respectively, Purely mechanical utility units like Watts are coherent.
The watt is a consistent unit of power, the base unit of length and time is the integer to the 10th power of the ratio of meters and kilograms (to keep the system “metric”), and the base unit of length and mass is the magnitude Convenient. for practical use. Since no one wanted to replace the second as the base unit of time, they kept the base units of length and mass as meters and kilograms.
The essentially mechanical practical units, like the watt, are coherent in the meter-kilogram-second system, but the explicitly electrical and magnetic units, like the volt, the ampere, etc., are not.This eliminates purely electrical and magnetic units.
Only by changing the meter-kilogram-second system differently by adding a fourth basic dimension to the existing three (length, mass, and time) can those units be made consistent with the meter-kilogram-second system (the previous three, plus one purely electrical one).
Difference Between Kilogram and Pounds
One kilogram of mass weighs approximately 2.20 pounds (pounds) on the surface of the earth. On the other hand, an object weighing 1 pound on the ground has a mass of about 0.454 kg.
Between kilograms and pounds, there are both qualitative and quantitative differences. Pounds, not kilograms, are used to describe weight, which is the force a mass applies to a barrier when there is an acceleration field operating perpendicular to the barrier. Figure 2 illustrates the weights of 2 kilograms, 5 kilograms, and 10 kilograms.
Figure 2 – Weights of 2 kg, 5 kg, and 10 kg
A mass of 1 kg weighs 0.814 lb on the surface of Mars, where the gravitational acceleration is 37% lower than on the surface of the Earth. A mass of 1 kg has no weight when in orbit or while coasting in space, where there is zero net acceleration.
Formula To Calculate Weight
There is no doubt that the mass of an item and the force of gravity on it affect its weight. This is why mass and weight are different. Whether an object was on the Moon or the Earth, its mass would be the same. On Earth compared to the Moon, an object would weigh differently as a result of gravity. So the formula will be
Weight = mass $\times$ gravity
Some Examples of Kilogram
Example 1
Find the weight of the person if the mass of the person is 60 kilograms and the gravitational force is 9.8 meters per square second.
Solution
As we know the formula for weight is equal to mass and gravitational force so from the statement mass of the person is equal to 60 kg and the gravitational force is equal to 9.8 meters per square second.
Weight = 60 $\times$ 9.8
Weight = 588 N
Example 2
The weight of a person on the moon is equal to 637 Newton, find the mass of the person if the gravitational force acting on the moon is 1.6 meters per square second.
Solution
According to the formula
Weight = mass $\times$ gravity
As the gravitational force acting on the moon is 1.6 meters per square second and the weight of the person on the moon is 637 N so
Mass=weight/gravity
Mass = 637/1.6
Mass = 398 kg
Hence the mass of the person is equal to 398 kilograms.
Example 3
Find the mass of the box illustrated in figure 3
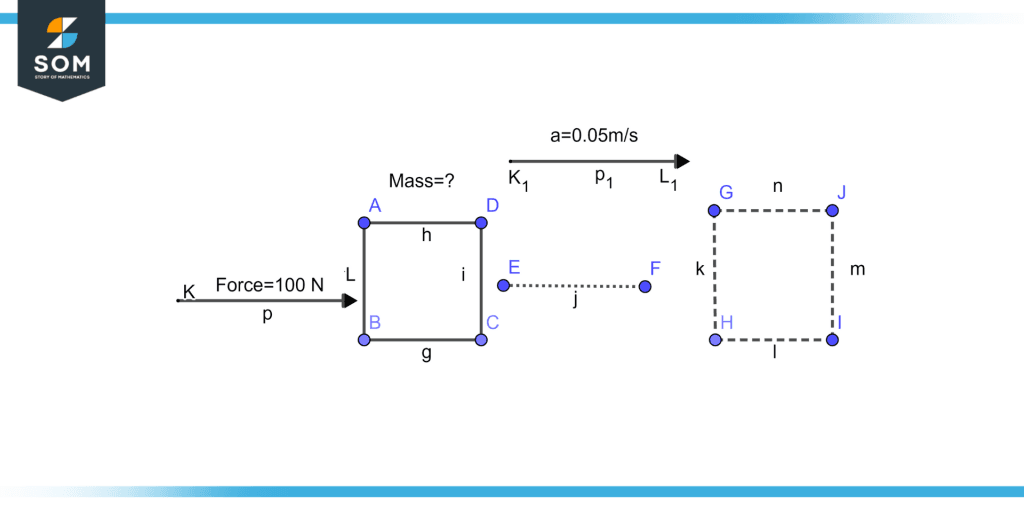
Figure 3 – Mass of a box.
Solution
Ass illustrated in the figure force applied on the object is 100 N and acceleration is equal to 0.05 m/s
Force = mass $\times$ acceleration
Mass = force / acceleration
Mass = 100/0.05
Mass = 2 kg
All images/ mathematical drawings were created using GeoGebra.
