Kilolitre Kiloliter|Definition & Meaning

Figure 1 shows a cube with a volume of one kiloliter. 

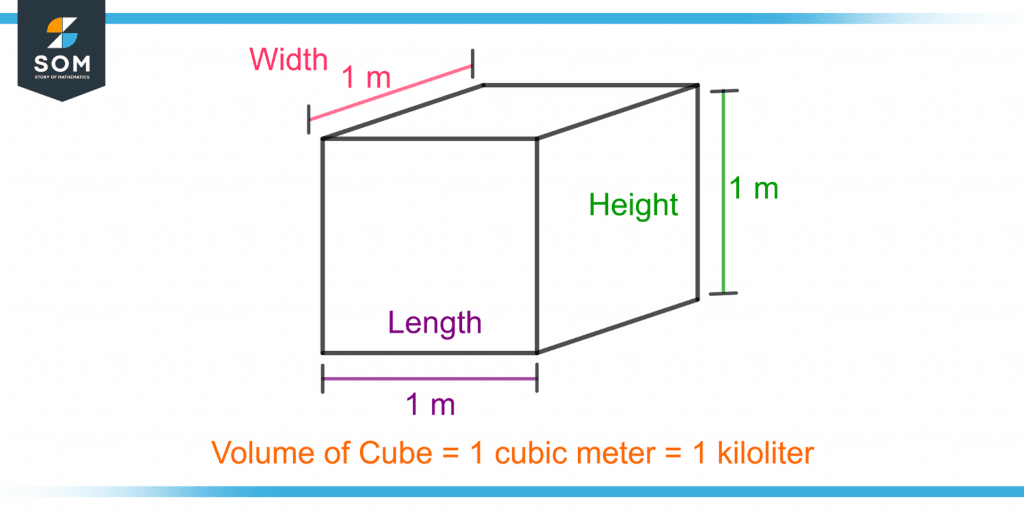
Figure 1 – Demonstration of One-Kiloliter Volume of Cube

A three-dimensional object with six square faces or sides with three faces joined by a common vertex is known as a cube.

A square is a two-dimensional shape with all sides of equal length. Therefore, a cube will also have all the sides of equal length.

The three dimensions of a cube are called length, width or breadth, and height. If a cube has a 1-meter length, width, and height, then the volume of the cube will be 1 cubic meter. It is calculated as follows:

Volume of Cube = Length × Width × Height

Volume of Cube = 1 × 1 × 1

Volume of Cube = 1 cubic meter = 1 kL

Volume

Volume is defined as how much space an object occupies. Only three-dimensional objects can have a volume. For two-dimensional objects, the area defines the space occupied on a plane. The volume is denoted by the letter “V.”

Concept

Volume can also be considered as how many cubes of 1 cubic meter volume (as shown in figure 1) are required to fill the given object. Consider the rectangular prism in figure 2.

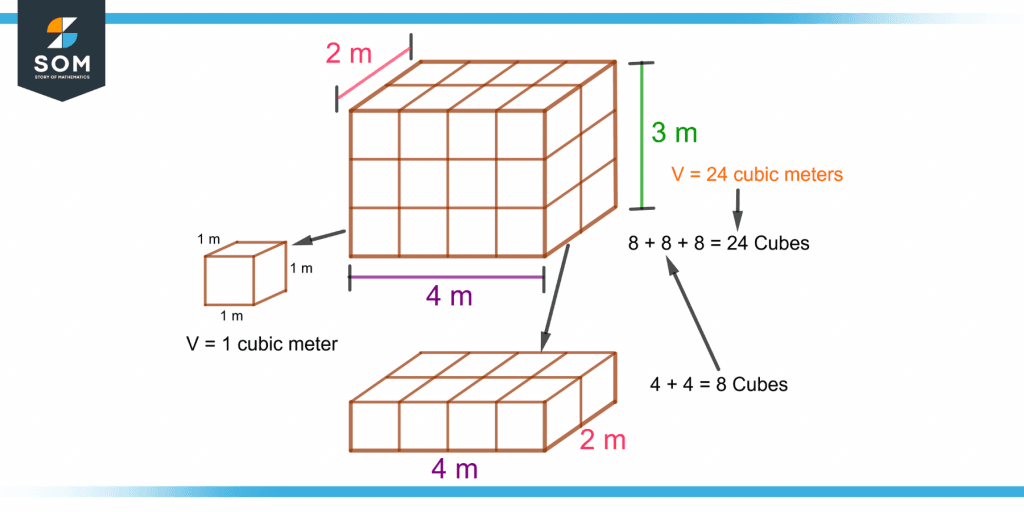
Figure 2 – Demonstration of the Concept of Volume of an Object

It has a length of 4 meters, a width of 2 m, and a height of 3 m. If the rectangular prism is cut from the bottom, the number of cubes in this part will be:

4 + 4 = 8

or

2 + 2 + 2 + 2 = 8

To calculate the total number of cubes, consider the height of the rectangular prism i.e 3 m. Adding 8 three times gives 24 that are the total number of cubes in the rectangular prism. The volume of 1 cube is 1 m$^3$, so the total volume will be 24 m$^3$ or 24 kiloliters.

Mathematical Formula

The volume of a solid or a liquid confined in a container is given by the formula:

V = SA × h

Where SA is the Surface Area of the solid and h is its height. The surface area is the space occupied by the surface of the solid. The height of the solid is the vertical length.

Volume of Different Solids

The cylinder and triangular prism volumes are discussed below.

Cylinder

A cylinder is three dimensional solid with a circle as its base. The volume is given as:

V = SA × h

The circular base has a radius r, so its surface area will be:

SA of Circle = πr$^2$

Substituting the surface area, the volume of cylinder will be:

V = πr$^2$ × h

Triangular Prism

A three-dimensional object with a triangle as its base is known as a triangular prism. The surface area of a triangle with a base b and height h is given as:

SA of Triangle = b × h/2

The triangle extends by a length l to make the triangular prism. So, the volume of the triangular prism will be:

V = (b × h/2) × l

Figure 3 shows a cylinder and a triangular prism.

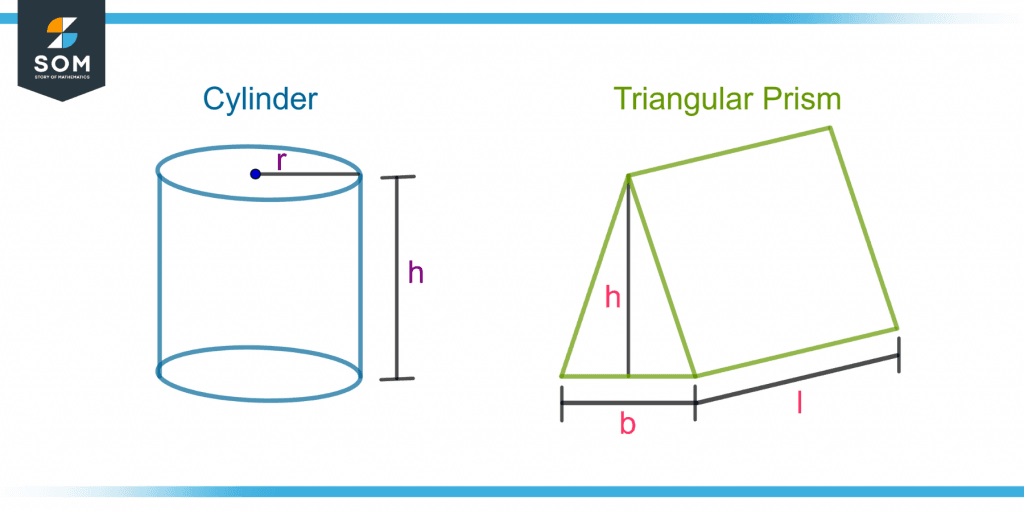
Figure 3 – Illustration of Parameters in Cylinder and Triangular Prism

Various Units of Volume in Kiloliter

Kiloliter can be expressed in the form of the following units.

Liter

Liter is a smaller unit than a kiloliter. One liter is equal to one-thousandth kiloliters as:

1 Liter = 1/1000 kiloliters

1 L = 0.001 kL

Multiplying 1000 on both sides gives:

1000 L = 1 kL

Or

1 kL = 1000 L

Items such as soda, milk, and other beverages are sold in liters.

Milliliter

The milliliter is even smaller than the liter. It is expressed as “mL” or “ml.” One milliliter equals one-thousandth liter:

1 milliliter = 1/1000 liters

1 mL = 0.001 L

It can also be expressed as:

1 L = 1000 mL

Also

1 kL = 1,000,000 mL

One milliliter is a minimal quantity. For example, a teaspoon can hold 5 milliliters of liquid.

Deciliter

Deci means “one-tenth.” One deciliter(dL) is equal to one-tenth of a liter:

1 deciliter = 1/10 Liter

1 dL = 0.1 L

Or

1 L = 10 dL

So

1 kL = 10,000 dL

Also

1 dL = 100 mL

Megaliter

Megaliter(ML) is a large unit as one megaliter is equal to one million liters:

1 ML = 1,000,000 L

ML can be used to measure the volume of water in lakes and rivers. Also:

1 kL = 0.001 ML

Figure 4 shows the ascending order of the volume units in liters.

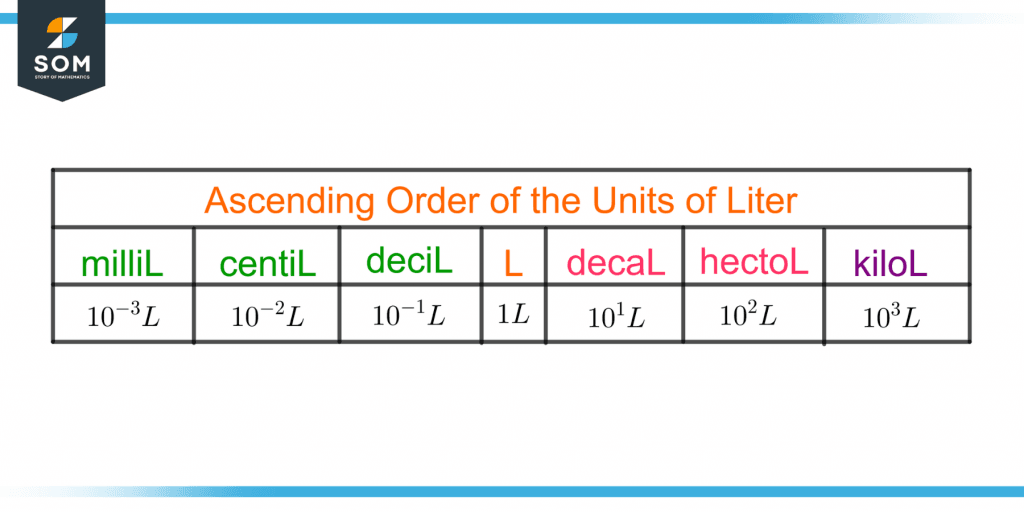
Figure 4 – Ascending Order of the Variations of Unit “Liter”

Different Units of Volume in Cubic Meter

Variations in the “cubic meter” and their relation with liters and kiloliters are discussed below.

Cubic Millimeter

One cubic millimeter (mm$^3$) is equal to one millionth of a liter:

1 mm$^3$ = 1/1,000,000 L

Therefore:

1 mm$^3$ = 1/1,000,000,000 kL

It can also be written as:

1 kL = 1,000,000,000 mm$^3$

Cubic Centimeter

A cube having one centimeter on each side is known as a cubic centimeter. It is denoted by cm$^3$ or cc. One cc is equal to one-thousandth of a liter:

1 cc = 1/1000 L

It can be written as:

1 L = 1000 cm$^3$

So:

1 kL = 1,000,000 cc

Cubic Kilometer

The cubic kilometer is a cube with all the sides equal to one kilometer(km). It is denoted by km$^3$. It is a large unit as 1 cubic kilometer equals one trillion liters:

1 km$^3$ = 1,000,000,000,000 L

Since 1 km$^3$ = 1,000,000,000 kL, we have:

1 kL = 1/1,000,000,000 km$^3$

Other Units of Volume

Volume can also be measured in bushels, gallons, pints, quarts, bushels, gills, cubic inches, and cubic feet.

Example of Kiloliter Units in Numericals

A cylinder has a diameter of 16 m and a height of 10 m. Calculate the volume of the cylinder in kiloliters and deciliters.

Solution

The volume of a cylinder is given by:

V = πr$^2$ × h

The radius is half of the diameter, so:

r = d/2 = 16/2 = 8 m

We also have the height:

h = 10 m

Calculating the volume by putting the values in the equation gives:

V = π(8)$^2$ × 10

V = (3.14)(64) × 10

V = 2009.6 m$^{3}$

As 1 kL = 1 m$^{3}$, so:

Volume = 2009.6 kL

To convert in deciliters, we have the following relation:

1 kL = 10,000 dL

So, the volume in deciliters will be:

V = 2009.6 kL = 2009.6 × 10,000 dL

Volume = 20,096,000 dL

All the images are created using Geogebra.

Kilogram Definition < Glossary Index > Kite Definition