JUMP TO TOPIC
Kite|Definition & Meaning
Definition
A kite is a quadrilateral exhibiting mirror balance when folded. Because of this balance, a kite possesses two similar inclinations and two sets of adjacent same-length sides. Alternatively, a Kite is a flat geometry having linear sides that consist of two pairs of identical-length adjoining sides.
The concept of the geometry of a Kite is shown in Figure 1.
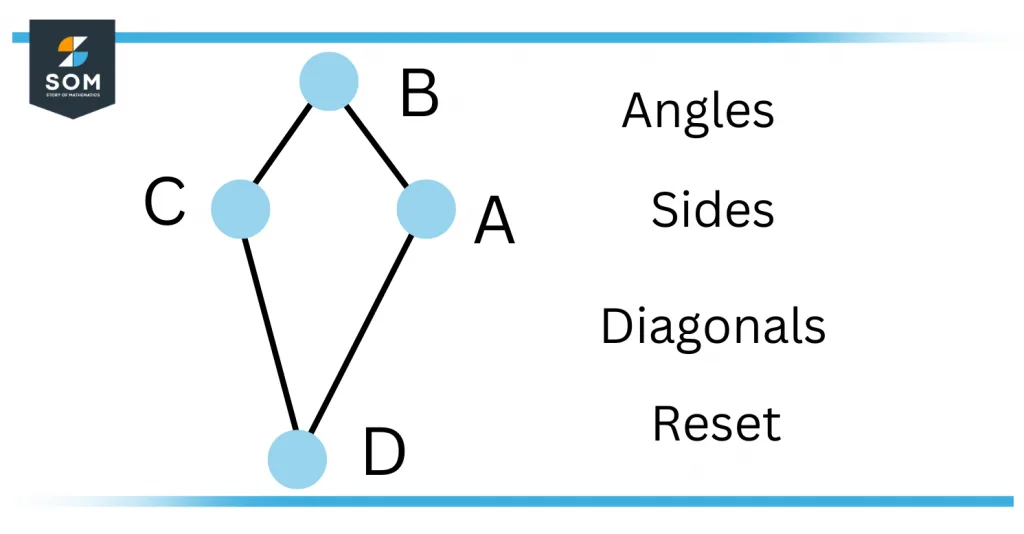
Figure 1: Shape of Kite
A quadrilateral itself has four corners and four sides, and four angles. The sum of all its internal angles is 360 degrees. A quadrilateral has sides that have different lengths and different angles. Squares, rectangles, etc., are particular types of quadrilaterals with some sides and angles equal.
A Kite is a balanced, closed figure having four linear sides such that there are:
• Two pairs of sides (in Figure 1, these pairs are AB-CB and AD-CD).
• Each pair of sides consists of two adjacent sides that are equal in length (in Figure 1, |AB| = |CB| and |AD| = |CD|).
The angles are equal where the pairs meet.
Kite Formulas
Area
The area represents the space enclosed by the Kite. The formula for area is given by:
Area (A) = (d1 × d2)/2
Where the variables d1 and d2 represent the length of diagonals. Suppose the diagonals are 12 m and 16 m in length; the kite area using the above formula, with d1 = 12 cm and d2 = 16 cm, turns out to be:
= (12 $\times$ 16)/2 cm$^2$
= 96 cm$^2$
Perimeter
Perimeter is the total distance covered while traveling along the sides of the Kite. The formula for the perimeter for Kite is given by:
Perimeter (P) = 2(x + y)
Where x and y are the lengths of the kite’s sides.
For example, suppose you want to find the perimeter of a kite whose side lengths are 10 and 16 cm. From the above formula, substituting x = 10 cm and y = 16 cm gives us:
= 2(10 + 16) cm
= 52 cm
Sides, Angles, and Diagonals of Kite
Sides of a kite
A Kite has two sets of sides that are congruent and the congruent pair of Kite sides are not opposing faces.
Angles of Kite
The angles subtended by the neighboring sides that are not congruent for the kite are always congruent.
Diagonals of a Kite
A kite has two diagonals that are perpendicular to each other:
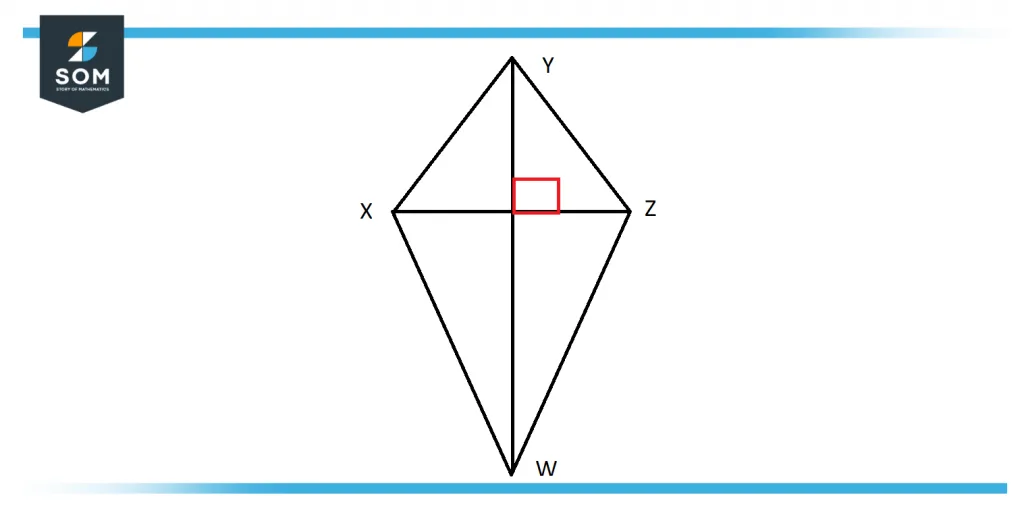
Figure 2: Diagonals of a Kite
For kite WXYZ as shown in Figure 2, XW $\cong$ ZW and XY $\cong$ ZY. Therefore, $\triangle$XYZ and $\triangle$YXZ are isosceles triangles that share a base, XZ. Based on this, we know that the line segment from W and Y to the midpoint of XZ is the height of $\triangle$WXZ and $\triangle$CBD. Therefore, diagonals WY and XZ are perpendicular. Diagonal WY is the perpendicular bisector of diagonal XZ.
Kite Properties
Kite has two diagonals that cross one another at right angles and is symmetrical around its major diagonal. Angles opposing the major diagonal in a Kite are of the same length. The Kite can be viewed as a set of congruent triangles having a standard base. The smallest diagonal splits the Kite into two isosceles triangles.
The diagonals of every Kite are at right angles. The types of Kites are described in the next sections. When a Kite is of convex type, the sides of the Kite are tangent to an inscribed circle. These include special cases i.e. the right kites, having two opposite right angles; the rhombi, which consist of two diagonal axes of symmetry; and the squares type of Kites, which are also special forms of Kite.
Following are some properties of Kite listed point-wise.
- The two angles of the Kite where the unequal sides meet are same.
- The Kite has two diagonals that cross each other at right angles.
- The large diagonal of the Kite bisects the other diagonal.
- A Kite is symmetrical about its large diagonal.
- The small diagonal divides the Kite into two isosceles triangles.
Types of Kite
Convex: The Kite is called convex when all of its interior angles are less than 180$^{\circ}$.
Concave: The Kite is called concave when at least one of its interior angles is greater than 180$^{\circ}$. For example, A dart or an arrowhead is a concave Kite.
Special Cases
Right Kites
The right kites are the Kites that have two opposite right angles. These Kites are cyclic quadrilaterals, i.e., there is a circle that crosses all their vertices. The right Kite is shown in Figure 3.
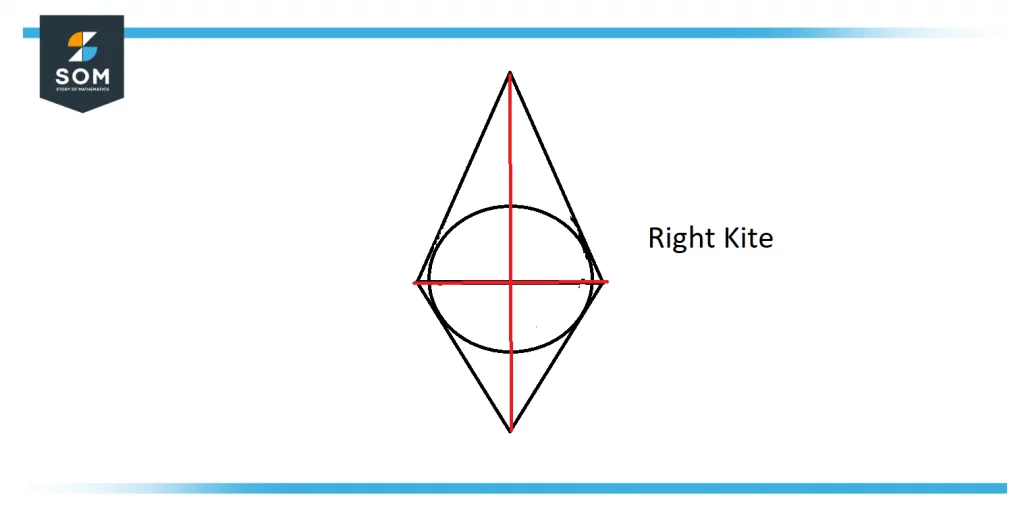
Figure 3: The Concept of the Right Kite
Equidiagonal Kite
Compared with all types of quadrilaterals, the form that has the largest proportion of its circumference to its dia is known as an equidiagonal Kite with certain angles. Four vertices of this kind of Kite lie at the three corners and another one at the side midpoints of the Reuleaux triangle.
A Special Kite
Most of the time, there exist two sets of congruent sides in a Kite that are not congruent, such a Kite is a rhombus that represents a special case of Kite geometry.
Duality
Kites and isosceles trapezoids can seem to be dual to each other, implying a resemblance between them that inverts the dimension of their parts, carrying vertices to sides and sides to vertices. From any kite, the carved circle is tangent to its 4 sides at the 4 corners of a trapezoid that is isosceles. This resemblance can also be seen as an example of polar exchange, a technique for finding connected points with lines and vice versa for a fixed circle.
Solved Examples of Problems With Kite-shaped Objects
Example
Find the area of a kite having diagonal lengths of 50 cm and 45 cm.
Solution
As stated above that the area of the kite is given as 1/2 ×( d1 × d2), therefore:
Required Area = 1/2 × ( 50 × 45)
Area =1125 cm$^2$
Example
The area of a kite-shaped field is 60 cm² and the length of one of its diagonal is 6cm. To cross the field, find the length one has to traverse.
Solution
Given that:
Area of a kite = 60 cm$^2$
Length of one diagonal = 6 cm
Kite Area = 1/2 × d1 × d2
60 = 1/2 × 6 × d2
d2 = 20 cm
That is, one has to traverse 20 cm.
All images/mathematical drawings were created with GeoGebra.
