Lateral|Definition & Meaning

What Is a Lateral? 

A lateral, in mathematical terms, is simply a side or surface that’s perpendicular to a base. This idea is used in the study of geometry to describe shapes and their dimensions.

Figure 1 – Lateral Surface is the slanted surface of any shape

For instance, in two–dimensional geometry, a lateral is a side that is perpendicular to a base and connected to it by two perpendicular lines. In three-dimensional geometry, a lateral is a surface that’s perpendicular to the base and connected to it by perpendicular lines.

We use the concept of laterals to describe a variety of shapes. For example, cones are three-dimensional shapes with a circular base and a single lateral surface that extends from the base to a point called the vertex. The lateral surface of a cone is curved and perpendicular to the base at all points. Similarly, in shapes like cylinders, pyramids, and prisms, the lateral surfaces are perpendicular to the base and connected to it by perpendicular lines.

Significance of Lateral Surface

The lateral surface is a type of surface that runs perpendicular to the main axis of an object. It’s one of three primary surfaces found on solid objects, with the others being the top and bottom surfaces. The lateral surface can often be thought of as the side surface of an object, but it can also refer to the outer surface of a cylinder or the circumference of a circular object. Understanding the properties of lateral surfaces is crucial for many industries, including engineering, design, and manufacturing.

When it comes to engineering, the lateral surface of an object is frequently exposed to outside forces and stresses, such as friction, wind resistance, and impact. As a consequence, it’s essential to evaluate the resilience and durability of lateral surfaces when designing and fabricating products. For instance, a product with a sturdy lateral surface will be better equipped to handle external forces and maintain its shape. In contrast, a product with a weak lateral surface may deform or break under pressure.

The lateral surface also plays a role in the design, specifically the appearance and style of an object. Designers might choose to add features or designs to the lateral surface to make a product look better or to set it apart from similar products. For example, a designer may add a unique pattern to the lateral surface to make a product stand out.

In the manufacturing industry, the lateral surface of an object can impact the production process as well. For instance, when machining a solid object, the lateral surface may need to be smooth and uniform to guarantee consistent and accurate measurements. Sometimes, the lateral surface may need to be treated with a special coating or finish to improve its strength or appearance.

Lateral surfaces also play a crucial role in the function of an object. For instance, on a cylindrical object, the lateral surface may act as a bearing surface, allowing the object to rotate smoothly. In these cases, the lateral surface must be smooth and free of defects to ensure proper function. Additionally, the lateral surface may serve as a surface for attaching other components or for attaching to a support structure.

Lateral Surface Area of a Cone

When it comes to geometry, there is a three-dimensional body that has a round base and a sharp-ended vertex, known as a cone. The lateral surface area of a cone directs to the area of the curved surface that extends from the circular base to the vertex. It is the portion of the cone that lies between the base and the slant height.

The slanted or lateral area of a cone can be easily calculated using the formula πrs, where r is the radius of the circular base and s is the slant height of the cone.

A = πrs

The slant height is described as the length between the vertex point and the point on the circumference of the base. In other words, it is the length of the line segment that links the apex of the cone to the boundary of the round base.

So, to put it all together, the equation to calculate the lateral surface extent of a perfectly symmetrical cone is π multiplied by the radius of the base multiplied by the slant height.

The lateral surface area of a cone comes out to be an important factor in specifying the general surface area of the cone. By using the formula πrs, it is achievable to calculate the exact lateral surface area of any cone, no matter the size or shape.

Lateral Surface Area of a Pyramid

A pyramid is a 3D geometric shape with a base and sides that meet at a point called the apex. The lateral surface area of a pyramid refers to the area of the pyramid’s sides, excluding its base. In other words, it’s the combined area of all the triangular faces of a pyramid.

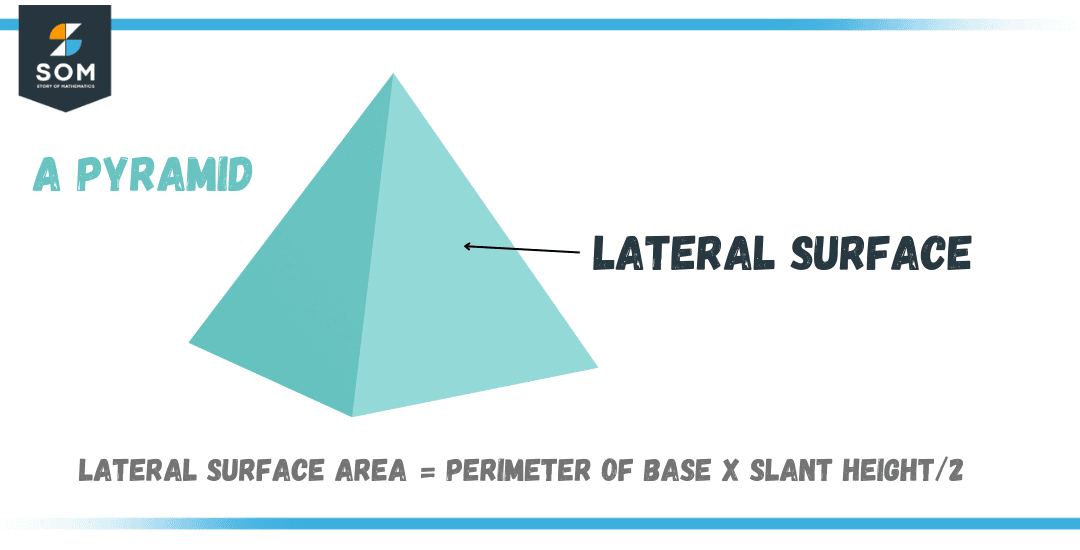
Figure 2 – Lateral Surface Area of a Pyramid

Now, here’s the formula for calculating the lateral surface area of a pyramid:

Lateral Surface Area = Perimeter of Base * Slant Height / 2

Where “Perimeter of Base” refers to the total length of the sides of the pyramid’s base, and “Slant Height” refers to the length of the side from the apex of the pyramid to the base.

Let’s put this formula into practice! Suppose we have a square-based pyramid with a base that measures 4 units long on each side and a slant height of 5 units. The perimeter of the base would be 4 * 4 = 16 units, and the lateral surface area would be (16 * 5) / 2 = 40 square units.

Lateral Surface of a Cuboid

In the case of a 3D cuboid shape, it is the combined area of all its faces, excluding the base. It’s like the total area of the four sides of the cuboid. The procedure to calculate the lateral surface extent of a cuboid is pretty simple. All you need to know is the length of any side of the cube, and you can easily find the lateral surface area by using the formula:

L.S Area = 4 x (Side Length)^2

It’s important to recall that the lateral surface area is not the same as the total surface area of a cuboid. The total surface area of a cube includes both the lateral surface area and the area of the base. To discover the total surface area, you just need to add the total area of the base to the lateral area.

Lateral Surface Area of a Prism

The lateral surface area of a prism can be considered as the combined area of all its rectangular sides, omitting the top and bottom faces. In simpler phrases, it’s the total area of the four sides of the prism.

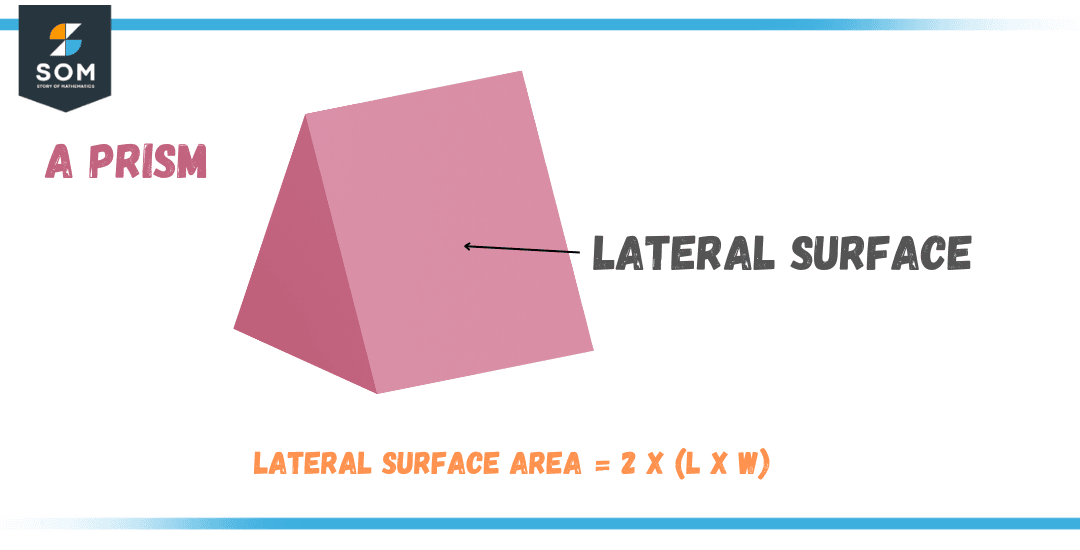
Figure 3 – Lateral Surface Area of a Prism

Calculating the lateral surface area of a prism is a straightforward process. The formula is just 2 times the product of the length and width of the rectangular sides. This can be written as:

L.S Area = 2 x (Length x Width)

It’s worth noting that the lateral surface area is not the same as the total surface area of the prism. The surface area is obtained by summing up the lateral area, the top area, and the bottom area.

Practical Uses of Lateral Surfaces

The idea of lateral surface area has a number of practical uses in various fields and industries. Here’s a closer look at a few:

Architecture: Architects use lateral surface area to figure out the quantity of material they need to cover the sides of their structures and buildings.

Engineering: In the field of engineering, the lateral surface area is used to work out the heat transfer and insulation requirements for equipment like pipelines and tanks.

Biology: Biologists use the surface-to-volume ratio, which is linked to the lateral surface area. It is employed to specify the quantity of oxygen, cells require and to calculate heat loss in living organisms.

Chemistry: Chemists utilize the surface-to-volume ratio in their calculations of chemical reaction rates. It is especially used in the case of catalysts and reaction vessels.

Environmental Science: Environmental scientists employ lateral surface area to find out how much pollutants can be absorbed by wetlands and other natural systems.

Agriculture: Farmers utilize the lateral surface area to estimate the size and volume of equipment, such as irrigation systems and storage tanks.

Solved Examples Involving Lateral Surface Areas of Different Shapes

Example 1

A cone-shaped grain silo has a wide area diameter equal to 20 m and a total elevation of 30 m. If the grain silo needs to be coated with a material to protect it from moisture, what is the lateral surface area that needs to be coated?

Solution

Given the diameter, we will determine the radius first.

The radius of the base can be calculated as

r = d/2

r = 20/2

r = 10 meters.

Using the formula of The lateral surface area of the cone:

A = πrs

A = 3.14 x 10 x √(10^2 + 30^2)

A = 628.3 square meters.

Example 2

A company is building a cylindrical oil storage tank to store crude oil. The tank has a diameter of 50 meters and a height of 60 meters. The company management requires us to keep in view that the tank is protected from the elements.

1. Determine the amount of material required to cover the lateral surface area of the tank.
2. If the material comes in rolls that are 5 meters wide and 20 meters long, how many rolls will the company need to purchase?

Solution

To begin, we need to calculate the lateral surface area of the tank. We can start by finding the radius of the tank, which is,

50/2 = 25 meters

Next, we can use the formula for the lateral surface area of a cylinder, which is

2πrh = 2 x 3.14 x 25 x 60 = 15140 m$^2$

Next, the company wants to determine the amount of material required to cover the lateral surface area.

First, we need to determine the total area that each roll can cover. This can be calculated as,

5 x 20 = 100 m$^2$

Next, we can divide the lateral surface area of the tank by the total area that each roll can cover to determine the number of rolls required. In this case,

15140 / 100 = 151.4

This means that the company will need to purchase 152 rolls of material to cover the lateral surface area of the tank.

All images are created using GeoGebra.

Kite Definition < Glossary Index > Least Common Denominator Definition