LHS|Definition & Meaning

Mathematics is a field that necessitates exactitude and deliberation at each and every stage of the problem-solving process. The left-hand side, also known as the LHS of an equation, is considered to be one of the most fundamental mathematical ideas. 

The portion of an equation that is located to the left of the equal sign (=) is referred to as the left-hand side of the equation. In order to effectively solve mathematical issues, it is essential to have a solid understanding of what the LHS represents and how it is incorporated into equations.

Figure 1 – LHS and RHS Equality representation

Before we can begin to comprehend LHS, we need to become well-versed in what an equation is, how it works, and the several types it might take.

An equation can be defined in a variety of different ways at any one time. An equation is a mathematical statement that demonstrates that two mathematical expressions have the same value. This is the most basic form of the definition of an equation in algebra. For example, the statement “2x + 4” equals 18 is an equation.

In this equation, the two expressions “2x + 4” and “18” are separated by the symbol for “equal.” Equations in algebra can be broken down into their most fundamental and fundamentally simple forms by using one or more variables.

Different Types of Equations

In algebra, the following are examples of some of the equations that are commonly used.

An Equation in Linear Form

An equation can have one variable, two variables, or even three variables, depending on the form it takes. The Standard equation for an equation with one variable and a linear form looks like this: ax + b = 0, where the constants are a and b, and x is the part of the equation with which we need to come up with a solution.

Similarly, the equation with two variables would look like this: ax + by + c = 0. where a, b, and c represent the constants, while x and y represent the variables in the equation.

Quadratic Equation

An equation of the second degree in algebra that involves the variable x or any other variable is called a quadratic equation. The equation for a quadratic in its standard form reads as follows: $ax^2 + bx + c = 0 $.

Here, a and b represent the coefficients, x represents the variable, and c represents the constant term. A non-zero value for the coefficient of $ x^2 $ is required as the first requirement for an equation to be considered a quadratic equation (a value greater than 0).

When expressing a quadratic equation in standard form, the $ x^2 $ term is written first, then the x term, and finally, the constant term is written. The order in which these terms are written is important. In most situations, the numerical values of a, b, and c are not expressed as fractions or decimals; rather, they are written as integral values.

Figure 2 – LHS and RHS of Quadratic Equation

Cubic Equation

This is an equation of the third order. When solving equations involving cubes, at least one of the variables needs to be raised to the exponent 3 level.

Rational Equation

An equation is said to be rational if it contains fractions with a variable, and either the numerator, the denominator, or both have fractions containing a variable.

In Mathematics, What Exactly Is Meant by “Lhs” (Left-hand Side)?

In mathematical equations, the component of the equation that represents the unknown quantity or the value that needs to be solved is (usually) located on the left-hand side of the equation. The LHS can be written as a mathematical expression that consists of variables, numbers, and operations on those variables and quantities.

For instance, the left-hand side of the equation x + 2 = 5 is written as x + 2. The value of x is an unknown number in this equation; the left-hand side of the equation represents the value that x must have in order for the equation to be correct.

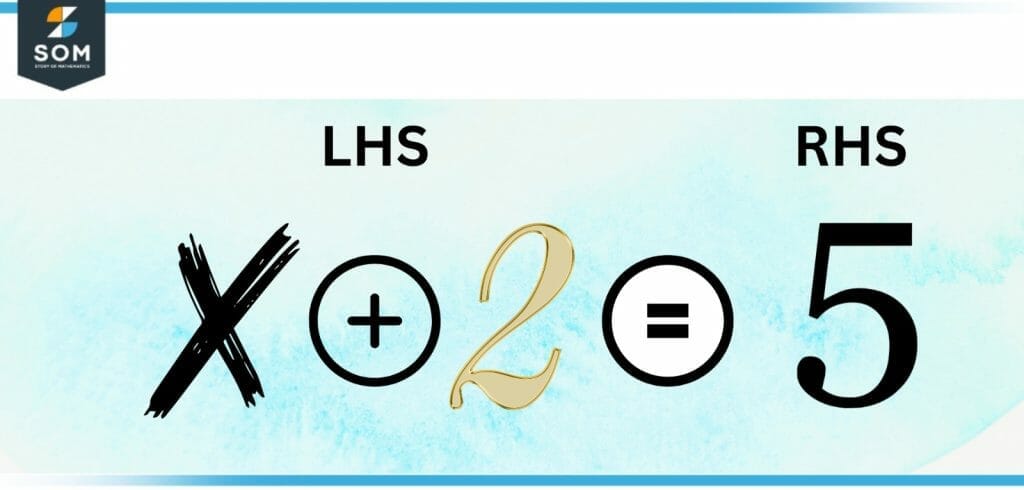
Figure 3 – LHS and RHS of a linear equation

Right-hand Side (RHS)

In equations involving mathematics, the portion of an equation that can be found to the right of an equal sign is referred to as the right-hand side (RHS) of the equation. The right-hand side of the equation displays the numerical value that the equation itself equals.

For example, in figure 2, the right-hand side of the equation x + 2 = 5 is the number 5. The right-hand side of the equation is the value that the left-hand side of the equation needs to be equal to for the equation to be valid.

How To Find LHS and RHS?

Right Hand Side (RHS) and Left Hand Side (LHS) are the two sides that make up every algebraic equation (LHS). In the context of an equation, the two sides, often known as the left side and the right side, are equivalent to one another. Let’s get a better grasp on this with the help of the LHS and RHS following example:

3x + 4 = 10

On the left-hand side of this equation, we have  3x + 4 = 10, and on the right, we have 10. We need to determine the value of the x in order to demonstrate that the LHS and RHS are equivalent.
Because of this, we will begin by presuming that the values on the left-hand side of the equation (LHS) and the right-hand side of the equation (RHS) are the same before moving the constant component of the equation to the RHS and solving it.

3x + 4 = 10

3x = 10 – 4

x = 6/3

x = 2

In the first equation that we constructed, we will now enter the number 2 for the variable x.

3x + 4

3(2) + 4

So, LHS is 6 + 4 = 10

Since we achieved 10 on the LHS and it was shown that the RHS  is also 10, We are now in a position to say that LHS is equivalent to RHS.

Importance of Understanding LHS in Mathematics

The left-hand side, or LHS, of an equation, is an important notion in mathematics since it assists in determining the value of the unknown quantity and lays the groundwork for finding a solution to the problem. To discover the answer to a mathematical issue, you must first determine the value of the variable that represents the unknown quantity and write it down on the left-hand side of the equation.

For instance, in the equation “x + 2 = 5,” the left-hand side is “x + 2,” and the variable that needs to be determined is “x.” You can determine the value that x should take for the equation to be correct by using the technique of “solving for x.” In this particular scenario, x has to be equal to 3 for x plus 2 to come out to 5.

The LHS is also significant in defining the type of mathematical operation that must be performed in order to solve a problem. For instance, if the left-hand side (LHS) of an equation is presented in the form of a subtraction problem, the solution to the equation would involve the application of subtraction.

In the event that the LHS is presented in the form of a multiplication problem, the equation can be solved by employing the multiplication operation. It is essential to have a solid grasp of the left-hand side of an equation in order to solve mathematical problems accurately.

Applications in Everyday Life That Make Use of the Lhs

The LHS is not only significant in the process of solving mathematical issues, but it also has applications in the real world.

Equations in mathematics are utilized to both solve difficult issues and generate accurate forecasts in a variety of professions, including engineering, finance, and design. In these areas, the left-hand side (LHS) indicates the unknown quantity or the value that needs to be solved, and the right-hand side (RHS) indicates the numerical value that the equation is equal to.

In the field of engineering, for instance, mathematical equations are utilized in the process of designing and constructing man-made structures like bridges and buildings.

In these equations, the left-hand side (LHS) represents the undetermined stress or load that a structure needs to be able to support, and the right-hand side (RHS) indicates the numerical value that the structure needs to be constructed to support.

In the field of finance, mathematical equations are frequently employed in order to generate forecasts on various financial markets and assets.

In these equations, the left-hand side (LHS) represents an undetermined return on an investment, and the right-hand side (RHS) represents the numerical value that the investment must return in order to be regarded as a successful investment.

Conclusion

Equations that are linear can take the form of one, two, or even three variables, depending on the situation. Determine the value of the variable in an equation with one variable as the first step in the process of solving the equation. The next step is to incorporate it into the first equation in order to determine whether or not the LHS and RHS are equal.

If the value of the variable that you found does not equate to the value of the other variable in the equation, either the value that you found for the variable is inaccurate, or the equation does not have a value that would equalize the two variables.

Example

As per the BODMAS rule, solve LHS for the equation: 10 + 5 – 3 = 3 x 4.

Solution

LHS = 10 + 5 – 3

LHS = 15 – 3

LHS = 12

Now, solving for RHS, we will get:

RHS = 3 x 4

RHS = 12

As we see LHS = RHS,  So the given equation 10 + 5 – 3 = 3 x 4 , is said to be in equality

All images/mathematical drawings were created with GeoGebra.

Least Common Multiple Definition < Glossary Index > Like Terms Definition