JUMP TO TOPIC
Like Terms|Definition & Meaning
Definition
Like terms in algebra are those that have the same variable to the same power.
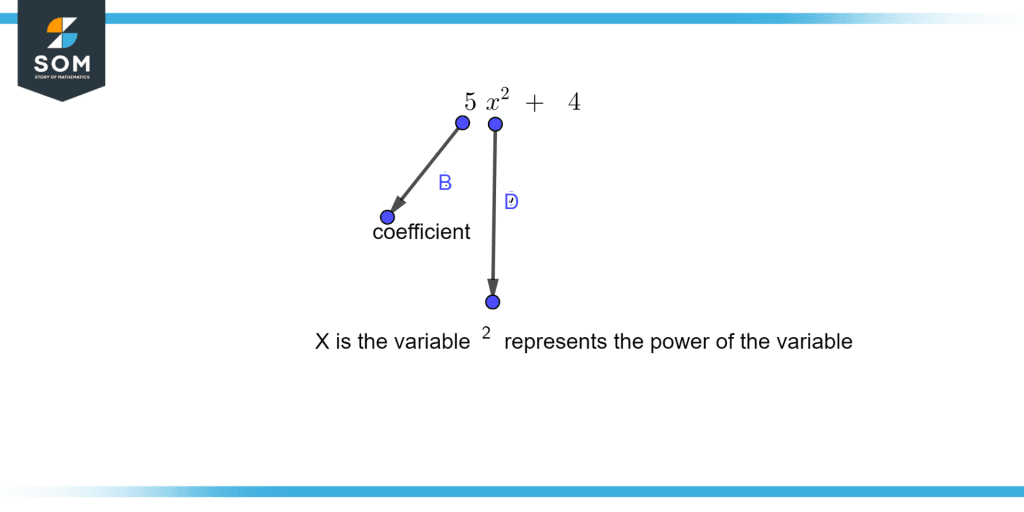
Figure 1 – Coefficient and variable
Figure 1 illustrates algebraic terms which elaborate the difference between the coefficient, variable, and its power.
The area of mathematics known as algebra is used to portray situations or problems using mathematical expressions. Tim’s grandmother, for instance, gave him several candy bars. He had five left after eating a few. Tim consumed how many candy bars, then? Since we know how many candy bars are still available, the number 5 is referred to as the constant. Numbers with a fixed numerical value are known as constants.
We’ll use the number x since we don’t know how many candy bars Tim’s grandmother handed him. Variables are represented by the letter x, which stands in for the unknowable amount. We can calculate how much he has consumed by deducting that amount from the total.
An expression that includes both variables and constants as well as an arithmetic operation like addition, subtraction, multiplication, or division is referred to as an algebraic expression in mathematics.
For instance: Three terms, namely 3x, 19y, and 30 make up the algebraic statement 3x + 19y = 30. The first two terms, 3x and 19y, are variables with 30 being a constant while x and y are both.
Thus, add or subtract marks that separate expression components, such as algebraic terms, are known as plus signs or minus signs.
The coefficient is the number that appears before a phrase. Since it is easier to write “x” and “1x” appears odd, we typically use “x” instead of “1x.” The symbols (variables) that we are accustomed to today were not used in algebraic expressions when they were first mentioned. Instead, a three-step algebraic expression construction process was used:
“Rhetorical algebra” was the initial phase. Equations were now expressed as whole phrases. For instance, “The object plus two equals three” is the rhetorical form of a+2=3. The ancient Babylonians set the groundwork for rhetorical algebra, which remained a popular method of algebraic representation until the 16th century.
Some symbolism emerged in the formulation of algebraic terms in the second stage, the Syncopated algebra. These did not, however, include all the traits of symbolic algebra.
For instance, using symbolic algebra, there is no restriction on the number of times an operation can be applied on one side of an equation. An algebraic expression with syncopation is first mentioned in Diophantus’ Arithmetica (third century AD), and then again in Brahmagupta’s Brahma Sphuta Siddhanta (7th century).
The last stage, often known as symbolic algebra, is how most of algebra is currently understood and is the point at which full symbolism emerged.
Although François Viète provided the foundation for the complete use of symbolism in algebra, some Islamic mathematicians like as Ibn al-Banna (13th–14th centuries) and al-Qalasadi (15th century) made contributions that can be seen as early steps toward this stage (16th century).
René Descartes (17th century) built on the idea that algebra might be used to represent and solve geometry issues at a later time and established the contemporary notation ( known to us as Cartesian geometry).
Mathematical Operations on Like Terms
Look at the formula 10×2 – 4×2, where the variables have the same exponent but different coefficients. This equation may be made even simpler by removing the identical variables from one another. This is conceivable because, even though the coefficients differ, the variables and exponents are the same.
Along with the variables and exponent values, the coefficients can be regarded as normal integers because they remain the same after subtraction. As a result, when the statement is simplified, we obtain 10×2 – 4×2 = 6×2. Combining comparable phrases is the process of making the expression simpler. It is easy to add like words; for instance, add 5z + 12z + 32z to get (5z + 12z + 32z) z.
Difference Between Like Terms and Unlike Terms
Like terms are the terms having the same exponents and variables. Similar concepts can be combined to make them simpler. Similar phrases can be added and subtracted together. A pair of phrases that are similar is 13×2 + 5×2.
Unlike terms are terms with different exponents and variables. Contrary terms cannot be made simpler by joining them. Contrary words cannot be added or subtracted together. Similar phrases include 7z and 25r. Dissimilar words are another name for unlike terms.
Some Example Problems Involving Like Terms
Example 1
Write the like terms in the expression x(x + 2) + x(5 + 3x) in simplest form.
Solution
In order to find the like terms, we have to simplify the expression for that purpose we have to multiply the variable x outside the bracket with inside terms then the expression will become x2+2x+5x+3x2 then all terms with variable x are combined 4x2+7x now the expression is 4x2 + 7x.
Example 2
Give the final expression after combining the same terms of the given expression
4x3+3x2+2x2+5x2+6x+3
Solution
According to the expression 4x3+3x2+2x2+5x2+6x+3, we have terms with the same variable and three different powers 4x3, 3x2+2x2+5x2 and 6x. We add all the like terms 3x2+2x2+5x2 which is equal to 10x2. The final expression is equal to 4x3+10x2+6x+3.
Example 3
Write the like terms in the expression x(x+2) +x(5x+3)+ 12 in simplest form.
Solution
In order to find the like terms, we have to simplify the expression for that purpose we have to multiply the variable x outside the bracket with inside terms then the expression will become x2+2x+5x2+3x2+12 then all terms with variable x are combined 4x2+7x now the expression is 4x2+7x+12.
Example 4
Give the final expression after combining the same terms of the given expression
5x3+3x3+2x2+5x2+6x+9
Solution
According to the expression 4x3+3x3+2x2+5x2+6x+9, we have terms with the same variable and three different powers 4x3+3x3, 2x2+5x2 and 6x. We add all the like terms 3x3+4x3 which is equal to 7x3. The final expression is equal to 7x3+7x2+6x+9.
Example 5
Illustrate the coefficients, variable, and power of the given expression
3x3+5x3+4x2+2x2+3x+3
Solution
First, we have to simplify the expression 3x3+5x3+4x2+2x2+3x+3 we have to add the like terms of x3 i.e., 3x3+5x3 which is equal to 8x3 and x2 i.e., 4x2+2x2 which is equal to 6x2 so the final expression will be equal to 8x3+6x2+3x+3. Figure 2 illustrates the coefficients, variables, and power of the given expression.
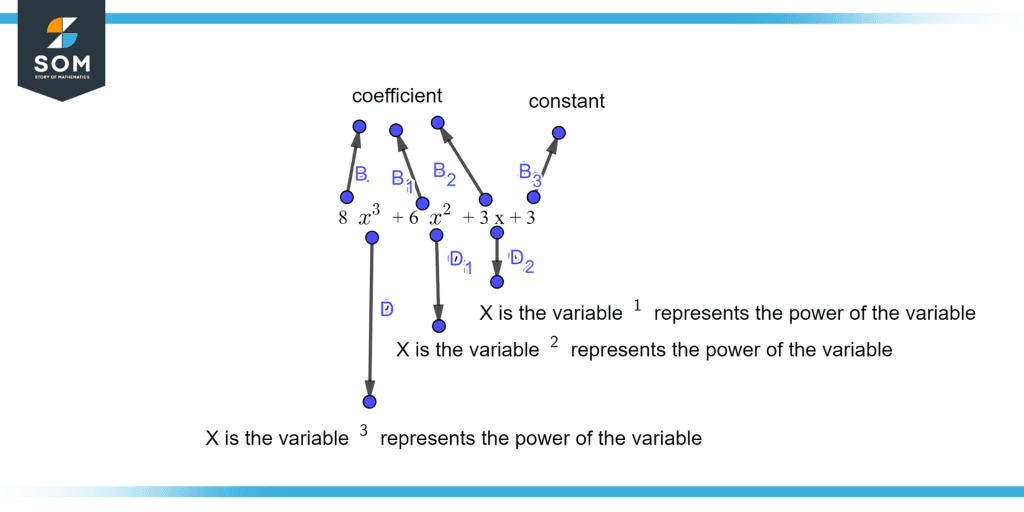
Figure 2 – Coefficient variable and constant of the expression
Example 6
Illustrate the like terms with different variables x and y in given expression
5x3+3x2+4+8y3+9y2
Solution
Figure 3 illustrates the like terms with variable x with coefficients 5 and 3 and like terms with variable y with coefficients 8 and 9.
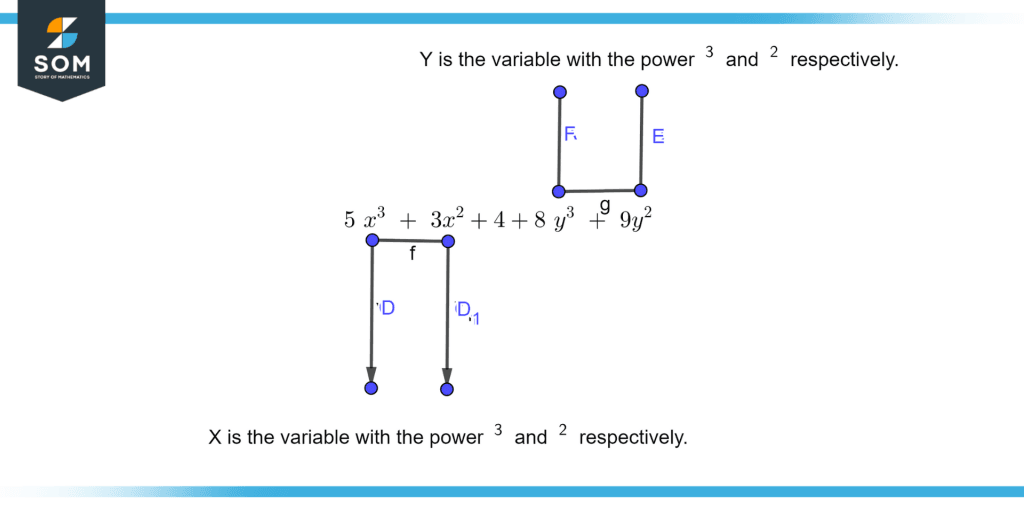
Figure 3 – Like terms with different variables
All images were created using GeoGebra.
