JUMP TO TOPIC
Line|Definition & Meaning
Definition
A geometrical one-dimensional object that joins two or more points through a straight path is called a line. A line has no thickness and has no endpoints. A line with endpoints is referred as a line segment.
y = mx + b is the equation of a line of the slope-intercept form, m being the slope of the line and b being the y-intercept.
A slope of a line is the ratio where the change in the y-coordinate is the numerator and the change in the x-coordinate is the denominator, between two points on a line. Two points on a line can define it and can be represented by the linear equation that passes through those two points.
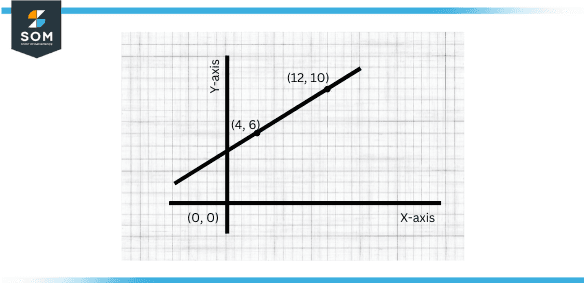
Figure 1: Straight line
In addition to its use in coordinate geometry, lines are also used in other areas of mathematics, such as calculus, where they are used to represent the graph of a function, and in geometric constructions, where they are used to create shapes and figures.
Drawing a Line
To draw a line in mathematics, you can use different forms of equations to describe it. Two common forms are the slope-intercept form (y = mx + b) and the point-slope form (y – y1 = m(x – x1)).
Slope-intercept Form
In this form, the line is defined by its slope (m) and y-intercept (b). To draw the line, you can start by plotting the y-intercept on the y-axis and then use the slope to determine the direction and steepness of the line.
Point-slope Form
In this form, the line is defined by a point on the line (x1, y1) and its slope (m). To draw the line, you can start by plotting the point on the coordinate plane and then using the slope to determine the direction and steepness of the line.
In both cases, once you have the equation of the line, you can plot the points that satisfy the equation and connect them with a straight line.
Overall, lines are a fundamental concept in mathematics that is used to represent geometric objects and to solve mathematical problems involving linear equations and functions.
Types of Lines
There are several types of lines that are used in different contexts. Some of the most common types of lines include:
Line Segment
A line segment is a piece of the line that has two distinct endpoints. It is a limited portion of a line, and it is defined by its two endpoints. A line segment can be represented graphically in a coordinate plane by plotting its two endpoints and connecting them with a straight line.
The distance between the two endpoints is known as the length of the line segment and can be calculated using the distance formula.
Straight Lines
A straight line is a line that extends infinitely in both directions and has no curvature. A straight line is usually represented by the equation y = mx + b, m being the slope of the line and b being the y-intercept.
Parallel Lines
Parallel lines are two or more lines that will always be at the same distance from each other and never meet, no matter their length.
- They are always at the same distance.
- They do not intersect.
- They have the same slope.
- They are always coplanar (in the same plane).
- The alternate interior angles of a transversal line crossing two parallel lines are congruent.
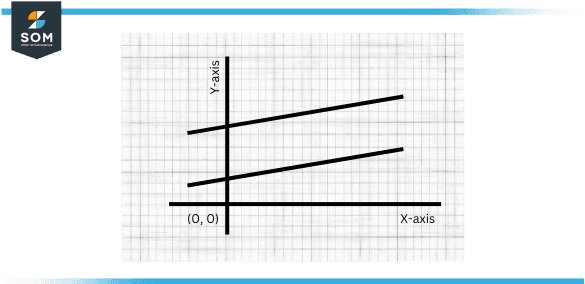
Figure 2: Parallel lines
Perpendicular Lines
Perpendicular lines are the two lines that intersect and form a “+” because they intersect at 90 degrees.
- The angle between two perpendicular lines is always a right angle at 90 degrees.
- They intersect at exactly one point.
- They form four right angles when they intersect.
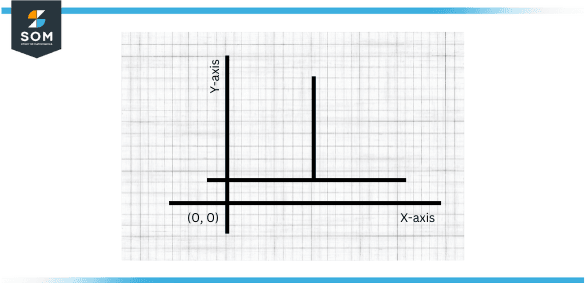
Figure 3: Perpendicular lines
Intersecting Lines
Intersecting lines can be two or more lines that will cross each other at one or more points. They intersect at least one point.
- The angles formed where intersecting lines meet are called vertical angles and are congruent.
- They have different slopes.
- They form four angles when they intersect.
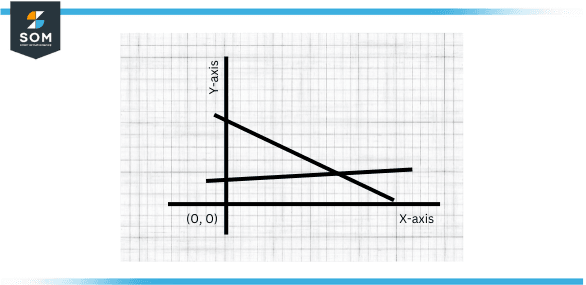
Figure 4: Intersecting lines
Horizontal Lines
A horizontal line is flat and goes left to right along the x-axis and has a constant y-coordinate. It has a slope of zero, and its equation is y = b, b being the y-coordinate of the line.
- They have a slope of zero.
- They are parallel to the x-axis.
- They have a constant y-coordinate.
- They are always equidistant from the x-axis (which is a line itself).
Vertical Lines
A vertical line is a line that runs from up to down along the y-axis and has a constant x-coordinate. It has an undefined slope, and its equation can be written in the form x = a, where a is the x-coordinate of the line.
- They have an undefined slope.
- They are parallel to the y-axis.
- They have a constant x-coordinate.
- They are always equidistant from the y-axis (which is a line itself).
Three Dimensional Lines
In three-dimensional space, lines are known as “lines in space” or “space lines.” They can be represented using different forms, such as parametric form, vector form, or symmetric form.
Parametric Form
A space line can be represented by a set of parametric equations, x = x1 + at, y = y1 + bt, z = z1 + ct, where (x1, y1, z1) being points on the line, (a, b, c) being the direction vector of the line, and t is a real parameter.
Vector Form
A point on the line can represent a space line and a direction vector, L: (x, y, z) = (x1, y1, z1) + t(a, b, c), where (x1, y1, z1) is a point on the line, (a, b, c) is the direction vector, and t is a real parameter.
Symmetric Form
A space line can be represented by the intersection of two planes, L: ax + by + cz + d = 0, where (a, b, c) is a normal vector of the line and d is a constant.
In three dimensions, lines can also intersect, be parallel or skew lines. A skew line is a line that is not parallel and not intersecting.
Example Question
What will be the equation of the line with a y-intercept of 5 and a slope of -2?
Solution
The slope-intercept form of the equation of a line is y = mx + b, where m and b are the slope and y-intercept, respectively.
Given the slope of -2 and the y-intercept of 5, we can write the equation of the line as:
y = -2x + 5
We can verify this by plugging in a point that lies on the line, for example (1,1):
y = -2(1) + 5 = 3
This equation represents a line that has a slope of -2 and a y-intercept of 5, which means that it has a negative slope (going down) and passes through the point (0,5).
All mathematical drawings and images were created with GeoGebra.
