JUMP TO TOPIC
Line Segment|Definition & Meaning
Definition
In geometry, a line segment is seized by two characteristic pinpoints on a line. Or we can also say that a line segment is a piece of the line that joins two points.
A line segment has two factual points in a line. The distance of the line segment is set, which is known as the length between two allotted points. The distance here can be calculated by metrical units such as centimeters (cm), and millimeters (mm) or also by traditional units like feet or inches.
Ray, Line, and Line Segment
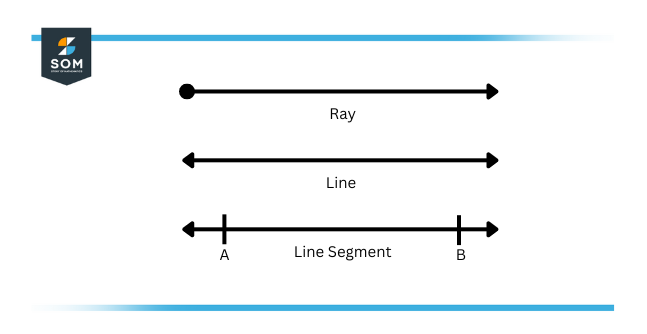
Figure 1 – Ray, Line, and Line Segment
A line has no terminal points and lengthens without limit in both paths while a line segment has two set or precise endpoints. The discrepancy between a Line segment and a ray is that a ray has only one terminal point and the other end of the ray grows infinitely or without any measure.
A one-dimensional form and cluster of points expanding immeasurably in both directions is known as a line. A portion of a line that has two endpoints or terminal points and there is a brief distance between them, is named a line segment. A ray starts at one terminal point and finishes at infinity. Figure 1 depicts the image of the ray, line, and line segment.
Important Notes
A line has undefined ends and therefore it cannot be estimated whereas, a line segment has a beginning point and an ending point, thus, it can be measured. Line segments have a specified length, consequently, they create the margins of any polygon. A ray has just one start point and no ending point, accordingly, it cannot be calculated.
The idea of rays can be comprehended with the sample of the rays of the sun, which have a start point but no stopping point.
Line Segment Definition
A line segment has two concrete stopping points in a line. The distance of the line segment is predetermined, which is the length between two set points. The distance here can be gauged by metrical units such as centimeters (cm), and millimeters (mm), or also by traditional units namely feet or inches.
A bounded line segment comprises both ending points, while an open line segment is the sole of the two ending points. A line segment that has exactly only one ending point is named a half-open line segment.
A line segment with two ending points, we say as A and B, is denoted by the bar character (—) such as $\overline{AB}$.
Measuring Line Segment
Given below are the methods we can use to calculate the Line segment.
By Observation
The easiest method of comparing the two line segments is simple observation. Just by watching these two line segments, one can easily foretell which is lengthy or tiny in contrast to the other.
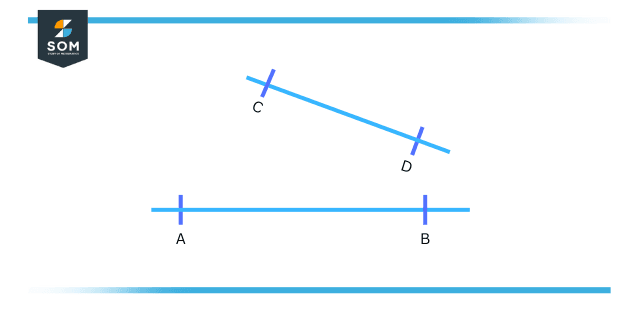
Figure 2 – Two Line Segments
In the above image, by observing it, we can say that line segment AB is more in the distance as corresponded to line segment CD. But this methodology has various limitations, every time we cannot depend entirely on observation to differentiate between two line segments.
Using Trace Paper
With the aid of trace paper, two line segments can be effortlessly juxtaposed. For this, firstly, trace one line segment and put it over on the second segment which is to be compared, and it can be readily concluded which is more significant in length. For more additional line segments, reprise the process repeatedly.
For accurate differentiation, the line segments must be outlined precisely. Therefore this procedure relies on the precision of outlining, which sets a constraint on this process.
Using Ruler and Divider
There are characteristic marks on the ruler starting from 0, as shown in the figure provided below. These arrangements separate the ruler into similar pieces. Each portion is similar to a distance of one cm, and these unit centimeters are also sectioned into ten portions, and each part is equal to one millimeter.
To calculate a line segment AB, put the 0 mark of the ruler on the edge of the start of the line and gauge its distance consequently.
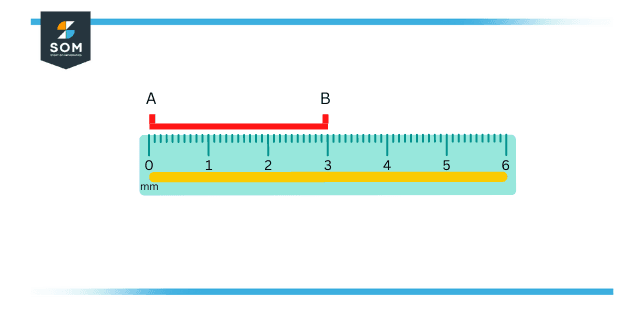
Figure 3 – Measuring Line using Rulers
In the picture given above, the distance of line segment AB is 3 cm.
To eradicate the location error we utilize a divider. Establish one needle of the divider at point A and the other at point B and then put the divider on the ruler and calculate its length. This approach is better authentic and unfailing.
Line Segment Formula
As we understand, a line segment has two ending points. Now if we comprehend the counterparts of the ending points, then we can also compute the distance of the line segment by the distance formula:
\[ D = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 }\]
Consider a line segment with the correlates (4, 2) and (–3, –4). Its line segment can be discovered as:
Consequently, by distance formula:
\[ D = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 }\]
\[ D = \sqrt{(-3-4)^2 + (-4-2)^2 }\]
\[ D = \sqrt{(-7)^2 + (-6)^2 }\]
\[ D = \sqrt{49 + 36}\]
\[ D = \sqrt{85}\]
\[ D = 9.219\]
Construction of Line Segment
Here we will understand to sketch a line segment with the aid of a compass and measuring scale or ruler. Let us presume, we require to sketch a line segment of a distance of 7cm. Then pursue the beneath-given steps:
- Sketch a line of any length without measuring it (keeping in attention the distance of the line segment)
- Draw a point A on the line, the beginning point of the line segment.
- Now utilizing a scale, discover the arrow of the compass 7cm apart from the pencil’s tip.
- Likewise, place the arrow of the compass at point P on the line, and with the exact measure draw an arc with the pencil.
- Now, call this point B
Thus, AB is the demanded line segment of length seven cm.
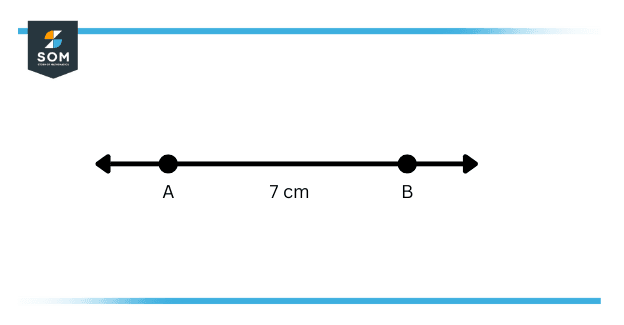
Figure 4 – 7 cm Line Segment
Examples of Line Segments
Mostly the dominant samples are noticed in 2D geometry, where per polygon is assembled by a sequence of line segments.
- A hexagon is created of 6 line segments united end to end
- A rectangle is created of 4 line segments
- A pentagon is constructed of 5 line segments
Thus, line segments achieve an essential role in geometry.
Line Segment: Solved Examples
Example 1
A line segment is provided by the endpoints (4, 2) and (10, –6). Measure its length.
Solution
Utilizing the distance formula for the procedure:
\[ D = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 }\]
\[ D = \sqrt{(10-4)^2 + (-6-2)^2 }\]
\[ D = \sqrt{(6)^2 + (-8)^2 }\]
\[ D = \sqrt{36 + 64}\]
\[ D = \sqrt{100}\]
\[ D = 10\]
All images/mathematical drawings were created with GeoGebra.
