JUMP TO TOPIC
Line Symmetry|Definition & Meaning
Definition
Line symmetry is another name for reflection symmetry which refers to a figure being identical to its reflection. It is called line symmetry due to the presence of a line which divides the figure into identical parts.
What Is Line Symmetry?
One sort of symmetry is known as line symmetry, and it is characterized by the fact that one half of an object mirrors the other half of the object across a line. If we want to put this concept into simple terms, we may state that if we use a line to divide an object into two equal pieces, then the two sides of the line will look the same.
Mirror symmetry and reflection symmetry are two other names for this type of symmetry. For instance, the top and bottom sides of a butterfly’s wing seem precisely the same, and the human face similarly exhibits line symmetry.
We will go through the definition of the idea of a line of symmetry here in this essay that we have written. In addition, we will investigate the line symmetry of various geometric shapes and count the number of lines of symmetry that each shape possesses. In addition, we will work through several examples so that you can get a better grasp on the topic.
One sort of symmetry that involves reflections is called line symmetry. It is referred to as line symmetry or reflection symmetry when at least one line in an object splits a figure into two halves in such a way that one half is the mirror image of the other half. This is the case when there is a line symmetry in an object.
The line of symmetry may run in any direction, including horizontally, vertically, diagonally, diagonally, and so on. A line of symmetry can therefore be thought of as an imaginary axis or line that divides a figure into two halves. Let’s have a look at the representation of a line symmetry presently.
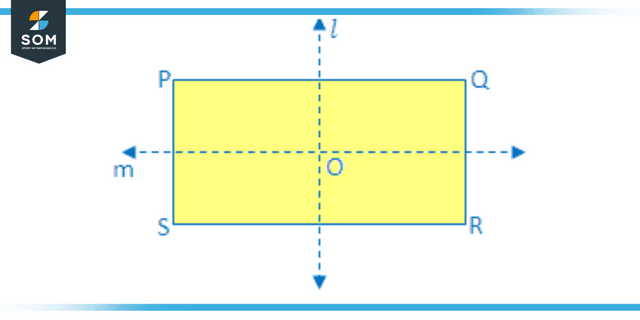
Figure 1: Representation of line of symmetry.
How Is Line Symmetry Represented?
The initial thing that needs to be verified is whether or not the object typically has a reflection of half. Consider folding a rhombus or squares along either line of symmetry; when you unfold it, each of the halves will perfectly match up with the other. This is an example of symmetry.
Therefore, for a shape to be categorized as either having line symmetry or mirrored symmetry, it must possess at least one line of symmetry. The fact that one of the two symmetrical halves follows lateral inversion gives rise to the phenomenon that is referred to as mirror symmetry.
Axis of Symmetry
A line that splits an object into two parts that are mirror images of one another is considered the line of symmetry or the mirror line. Now that we have a square, we may fold it into two halves, each equal in size. When a pattern is folded in half along its line of symmetry, the resulting halves are identical to one another when viewed from either side. The term “axis of symmetry” refers to this particular line of symmetry.
Types of Line Symmetry
Based on the direction of the line of symmetry, it is possible to classify it as one of the following:
Vertical Line Symmetry
The line of symmetry that runs vertically across reveals that the figure can be cut in half along a fixed straight line to create 2 halves that are mirror images of one another. In this particular instance, the line of symmetry will be horizontal.
Horizontal Line Symmetry
When the shape in question is cut horizontally, it can be observed that it is possible to separate it into two halves of equal size. This is an example of a horizontal line of symmetry. When anything like this happens, the line of symmetry will be horizontal. When a shape is split horizontally, sliced from right to left or vice versa, the horizontal line of symmetry will divide the shape into two identical halves.
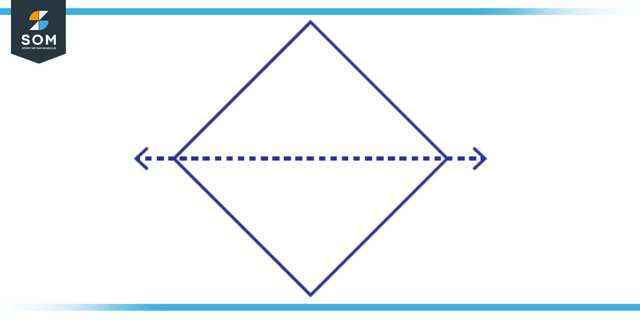
Figure 2: Representation of horizontal line of symmetry.
Diagonal Line Symmetry
The line of symmetry known as the diagonal line can be seen in the shape that was just described by seeing how it can be divided into 2 halves that are mirror images of one another by cutting it at the corners. In this particular instance, the line of symmetry takes the form of a diagonal. When a shape is cut along its diagonal symmetry line, it is split into two identical halves.
Line Symmetry in Shapes
In geometry, there are plane shapes that have line symmetry. Some examples of these plane shapes include the square, rectangle, triangle, rhombus, and parallelogram. There is a list of some of the more common examples of lines of symmetry in shapes that are just two dimensions:
Square With a Symmetry of Lines
The four lines of symmetry in a square are made up of the lines that pass through the opposing vertices and the lines that pass through the center points of the opposite sides. Therefore, a square has one line of symmetry running vertically, one line running horizontally, and two lines running diagonally.
The Symmetry of the Lines in a Rectangle
A rectangle has two symmetry lines, which pass through the midpoints of the sides that are opposite one another. The shape that results from folding a rectangle along one of its diagonals does not have perfect symmetry. Therefore, a rectangle has only one line of symmetry running vertically and one line horizontally.
Triangle With Symmetry Along Its Lines
The symmetry of the lines that make up a triangle is determined by its sides. In a scalene triangle, there is no line symmetry present. If a triangle is isosceles, it has at least one line of symmetry; if a triangle is equilateral, it has three lines of symmetry. If a triangle is not isosceles, it has no lines of symmetry.
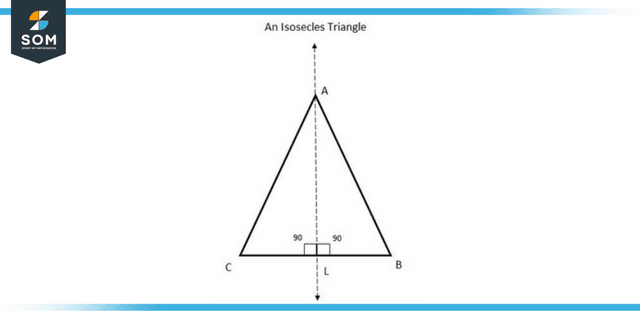
Figure 3: Representation of the line of symmetry of an isosceles triangle
Rhombus Exhibiting Line Symmetry
Two lines of symmetry can be drawn on a rhombus. The rhombus’s lines of symmetry are formed by the two diagonals that make up the shape.
Examples of Line Symmetry
Example 1
How many lines of symmetry are there in a square?
Solution
There are four lines of symmetry in a square: 2 along the diagonals and 2 along the midpoints of the two pairs of opposite sides.
Example 2
How many lines of symmetry are there in a regular hexagon?
Solution
There are six lines of symmetry in a regular hexagon: 3 along the midpoints of the three pairs of opposite sides and 3 along the lines joining the 3 pairs of opposite vertices (diagonals).
All images/graphs are created using GeoGebra.
