JUMP TO TOPIC
Magnitude|Definition & Meaning
Definition
The phrase “how much of something” essentially defines “magnitude,” a term that defines the intensity or value of a quantity. For instance, we can use it to explain why a car and bicycle’s speeds cannot be compared directly.
We can also use magnitude to describe the distance covered by an object or the quantity or amount of an item.
Both scalar and vector quantities have magnitude, though vectors additionally describe the direction.
What Is Magnitude?
The greatest extent of an object’s size and the direction it extends is called its Magnitude. Scalar and vector quantities can be related using Magnitude as a common factor. We know quantities with Magnitude only are referred to as scalar quantities because this is how the term is defined. Whereas vector quantities have both Magnitude and direction, scalar quantities have Magnitude only.
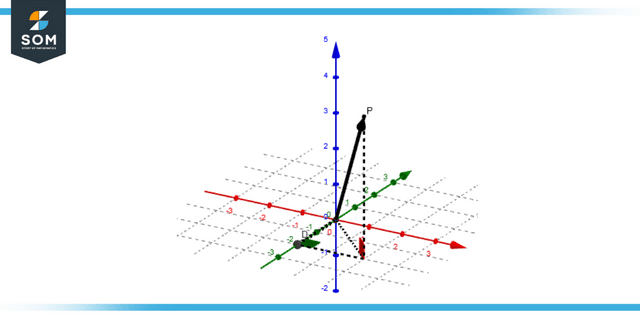
Figure 1: 3D representation of vector magnitude
The concept of Magnitude can be applied in a variety of different ways. A few of them are as follows:
- The intensity of the earthquake
- The amount of charge carried by an electron
- The extent of the force
- Magnitude of displacement
- The magnitude of the force of gravitational attraction
A Real-life Example: Earthquake’s Intensity
An earthquake’s length, breadth, and width are the dimensions used to define its Magnitude. It is determined by the Magnitude of the earthquake’s actual physical effects. It is generally agreed that there is just one Magnitude for earthquakes.
The Magnitude of the shaking induced by the earthquake varies from one location to another due to several factors, including the nature of the surface material and the geographic location relative to the epicenter. Both whole numbers and fractional representations of whole numbers can be used to express the Magnitude of an earthquake.
If an earthquake has a magnitude of 5.3, then it is considered to be of moderate intensity. When the Magnitude of an earthquake reaches 6.3 or higher, it is considered a powerful earthquake.
An Electron Carrier
The Magnitude of the elementary charge, denoted by the letter e with a minus sign, is equivalent to the charge that an electron carries. 1.6022 x 10-19 C is the value that corresponds to the elementary charge.
Positive and negative electric charges are the two sorts of charges that are known to exist, according to what we know. The positively charged particles are referred to as protons, and the negatively charged particles are referred to as electrons. If there are more protons in an object than electrons, that object is said to have a positive net charge.
Similarly, we say that an object has a negative net charge if it has a more significant number of electrons than protons. And if electrons are equal to protons it’s called neutral.
The Force’s Absolute Magnitude
The term “magnitude of force” comes from the field of physics and refers to the total of all the forces operating on an object. When all forces are moving in the same plane, the overall force exerts more pressure. When forces operate on an object from various directions, the overall amount of force exerted on the object is reduced.
Magnitude of Vector
As is common knowledge, a vector is an item that possesses both the Magnitude and the direction of the vector’s parts. Calculating the length of a vector is a necessary step in determining its Magnitude; see also Magnitude. Quantities like speed, direction, power, momentum, etc., are vector terms. But velocity, weight, distance, volume, temp, etc., are scalar quantities.
Scalars only have Magnitude, whereas vectors have both Magnitude and direction, and scalars only have Magnitude.
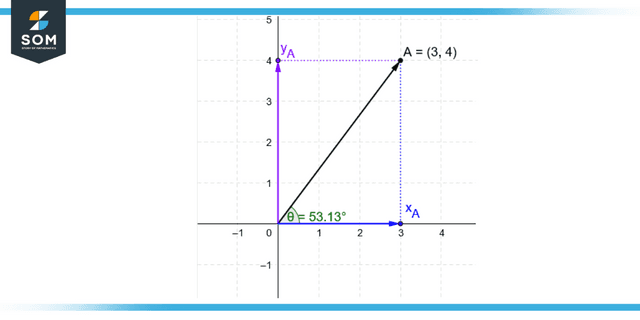
Figure 2: Representation of magnitude of vector.
Measurement of the Displacement
The shortest distance that can be traveled from the object’s original position to its ultimate position is used to define the Magnitude of the displacement. When referring to a particle moving across space, the Magnitude is always either smaller than or equivalent to the distance covered.
When the particle is moving down the one-dimensional pathway, the amplitude of the displacement is equal to the entire path length that the particle travels in the allotted time. This is because the path is only one-dimension long.
Complex Number
Take into consideration the complicated number a plus bi. Imagine the complex number obtained by plotting in the complex plane. We have the real axis and the imaginary axis, and the number a + bi is the point (a,b) where an is the location along the real axis and b is the location along the imaginary axis.
Finding the magnitude of the complex number is as simple as finding the point at which the real and imaginary axes intersect. After that, we can determine how big the complex number a + bi is by determining the distance between the point (0,0) and the point on the complex plane. This will give us the Magnitude of the complex number (a,b).
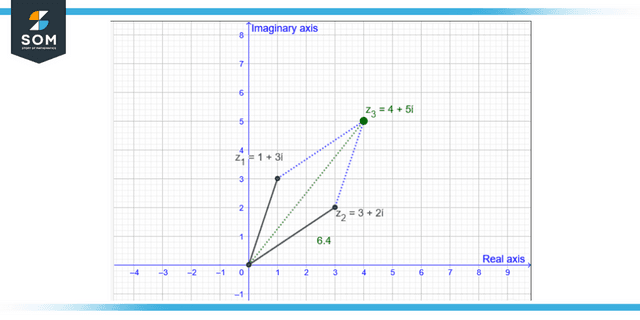
Figure 3: Representation of magnitude of complex numbers.
Is Magnitude Always Non-negative?
How significant is a negative number like -6? What does that mean in terms of its Magnitude? The answer is (positive) 6. Magnitudes cannot be negative.
Consider the concept of Magnitude as a measurement of size: it does not appear that there is a logical concept of a size smaller than zero. To make sense of this, one must first comprehend that the Magnitude of -10 is more significant than that of -9, although -10 is a lower figure.
When dealing with negative numbers, the order of Magnitude flips, and counting moves in the reverse direction on the line segment, precisely as with negative values.
Example 1
Consider a vector AB whose coordinates are x = 5, y = 2, z = 8. Find the magnitude of vector AB.
Solution
The magnitude of the vector AB can be calculated by adding the square of each coordinate and then taking the square root of the answer.
(5)2 + (2)2 + (8)2 = 93
(93)1/2 = 9.64
Example 2
Find the distance between two points with coordinates R (4, 7, 1) and S (-2, 6, -3).
Solution
If d is the distance between two points (x1, y1, z1) and (x2, y2, z2) then:
d2 = (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2
Now putting the values:
d2 = (-2 – 4)2 + (6 – 7)2 + (-3 – 1)2
= 53
d = (53)1/2 = 7.2
All images/graphs are created using GeoGebra.
