JUMP TO TOPIC
Major Arc|Definition & Meaning
Definition
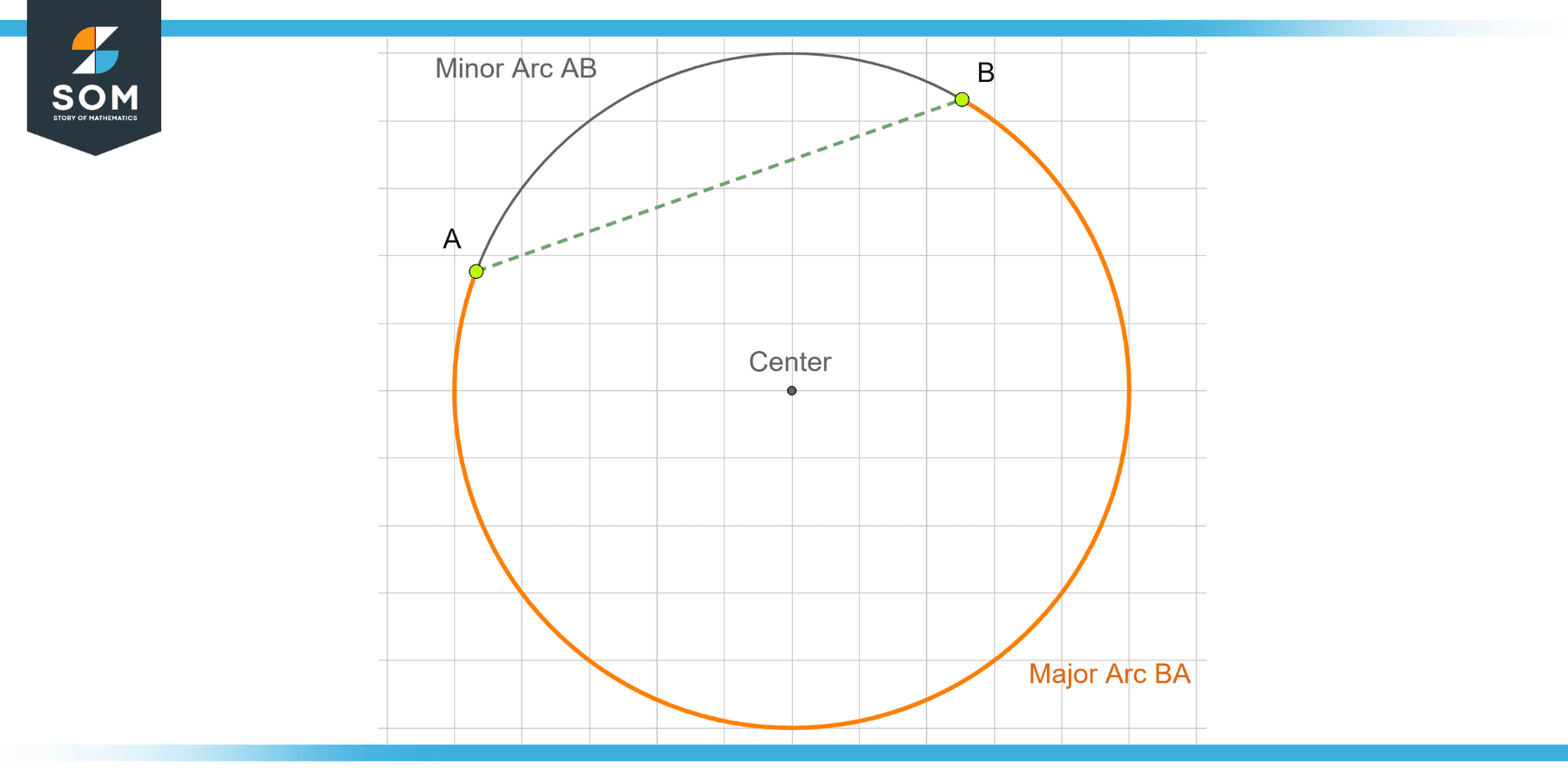
The lengthier of the two arcs joining any two points on a circle’s perimeter is the major arc, while the shorter one is the minor arc.
Figure 1 – The major and minor arcs between points A and B on a circle.
What Is an Arc?
An arc is a line curved around a single point. In geometry, the term refers to a part of a circle’s circumference (i.e., its boundary). Therefore, the length of any arc of a circle is always smaller than its circumference.
Forming an arc requires two distinct points on the circle. Let us call these two points A and B. The part of the circle between these two points is arc AB. We can calculate the arc’s length with the formula:
l = r x θ
Given that O is the center of the circle, then l is the arc length, $\boldsymbol{\mathsf{\theta}}$ is the angle in radians between the two radii (OA and OB) bounding it, and r is the value of the circle’s radius. We illustrate these parts of the equation in Figure 2 below.
Why Do the Major and Minor Arcs Exist?
Because there are two ways to traverse a circle (clockwise or anti-clockwise), there are two ways of describing the resulting arc AB. You could go clockwise or anti-clockwise from A to B, resulting in distinct arcs with different lengths.
Usually, one of these two arcs is longer than the other one. Whatever the case, the sum of the two arcs’ lengths always equals the circumference.
Major and Minor Sectors and Segments
Sectors and segments represent the inner portions of the circle in addition to the outer boundary (the arc). Again, since the circle splits into two parts, we have the concept of major and minor sectors and segments. If the arc AB was a major arc, the corresponding segment and sector are the major segment and sector, and vice versa.
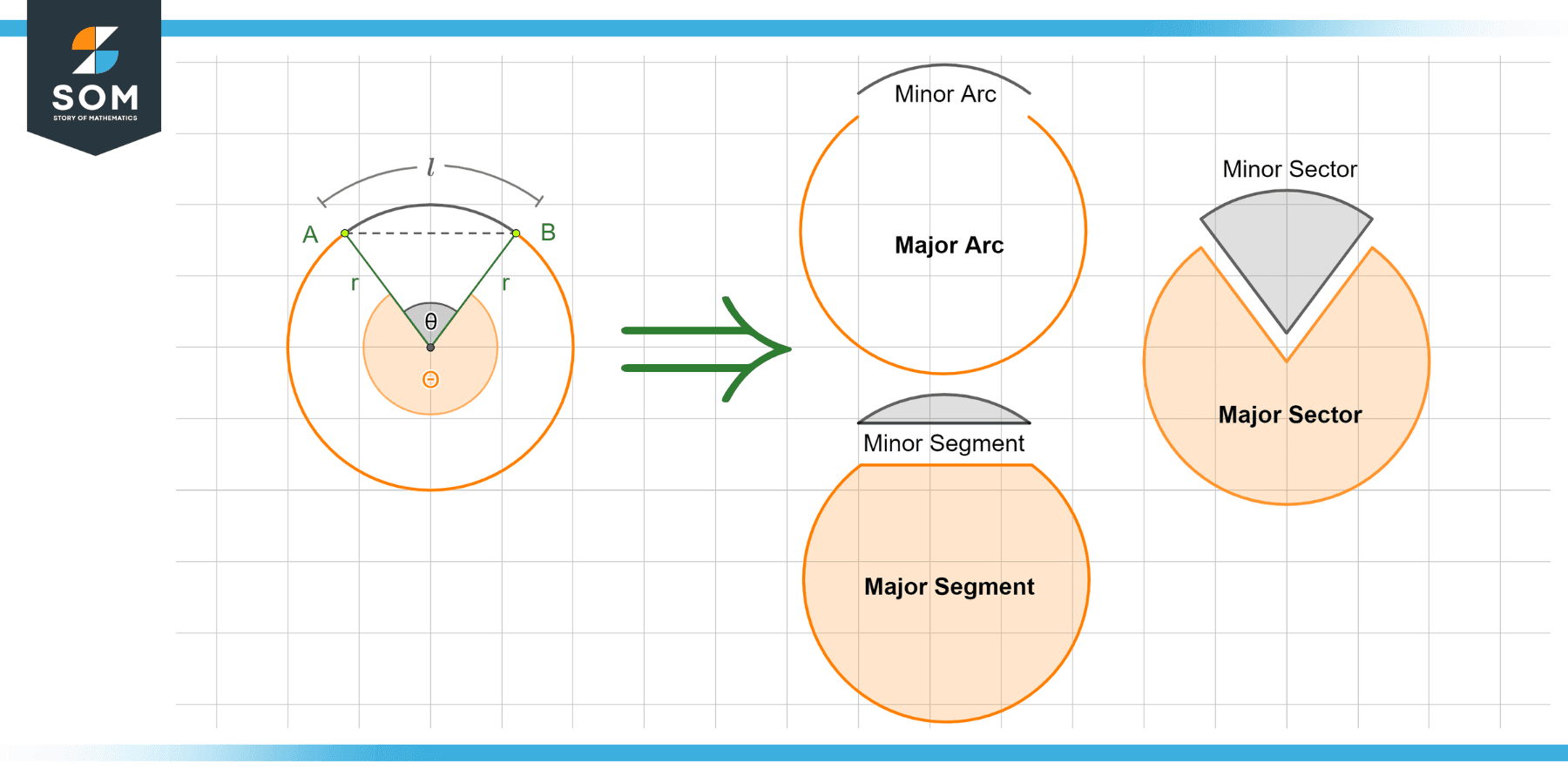
Figure 2 – The major and minor arcs reuslting in major and minor segments and sectors.
Note:
area of major segment + area of minor segment = area of the circle
area of major sector + area of minor sector = area of the circle
The segment AB of a circle splits it into two parts about a chord joining points A and B. The result looks like two different semicircles. For example, when you cut a cake in a straight line such that the two halves are not equal, you have two segments of the cake.
area of segment (θ in radians) = $\displaystyle \mathsf{\left( \frac{\theta-\sin(\theta)}{2} \right)}$ x r2
On the other hand, the sector is the region enclosed within the arc and the bounding radii OA and OB. For example, when you cut a pizza into many slices, you normally cut it into sectors.
area of sector (θ in radians) = $\mathsf{\dfrac{\theta}{2}}$ x r2
If the angle is in degrees, replace θ in the formula with the following (except in sin(θ), keep your calculator in degree mode for that):
\[ \mathsf{\theta \textsf{ (in rad)} = \dfrac{\theta \textsf{ (in deg)} \times \pi}{180}} \]
The Semicircle – A Special Case
The circle divides into two semicircles when the major and minor arc lengths are equal. Therefore, there is no distinction between major and minor segments and sectors in a semicircle. All of them occupy the same area. Further, the sector and segment of a semicircle physically represent the same region (this is not the case in any other scenario).
A Few Solved Examples to Clear Things Up
Example 1
Consider the unit circle (radius = r = 1 unit) centered at the origin, as shown in the figure below.
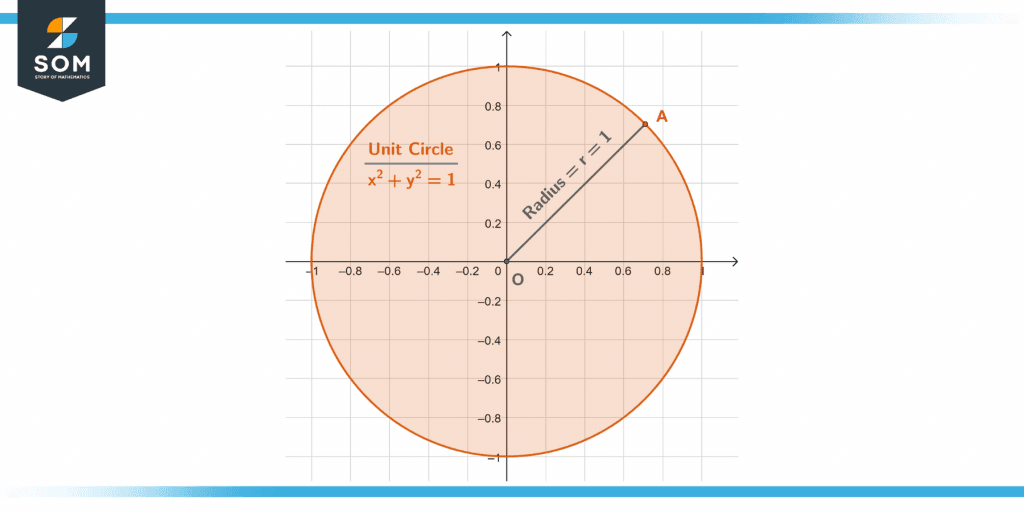
Figure 3 – The unit circle used in the following examples.
Find the clockwise arc between the point y = 0.5 in the second quadrant and the point x = 0.3 in the fourth quadrant. Is this arc major or minor?
Solution
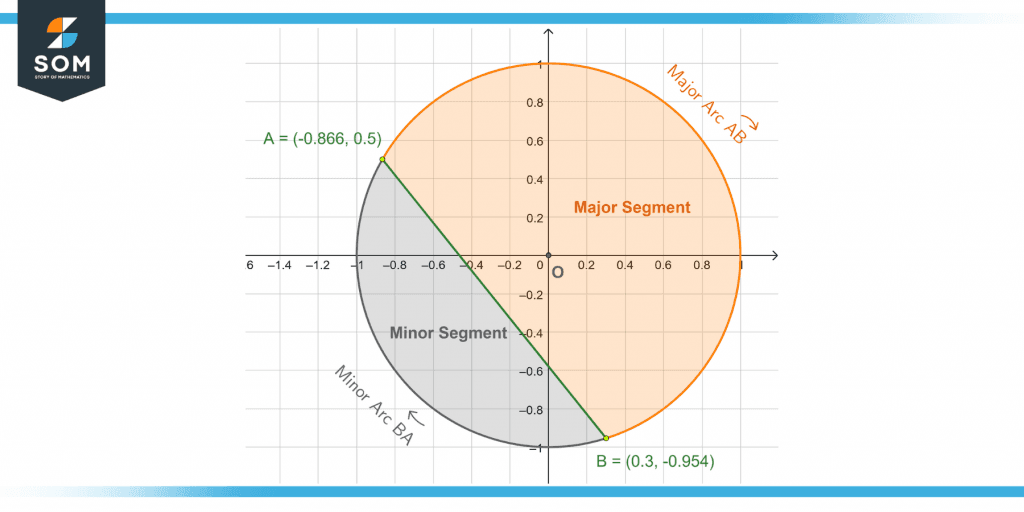
Figure 4 – The first example’s major and minor arcs and segments from points A and B.
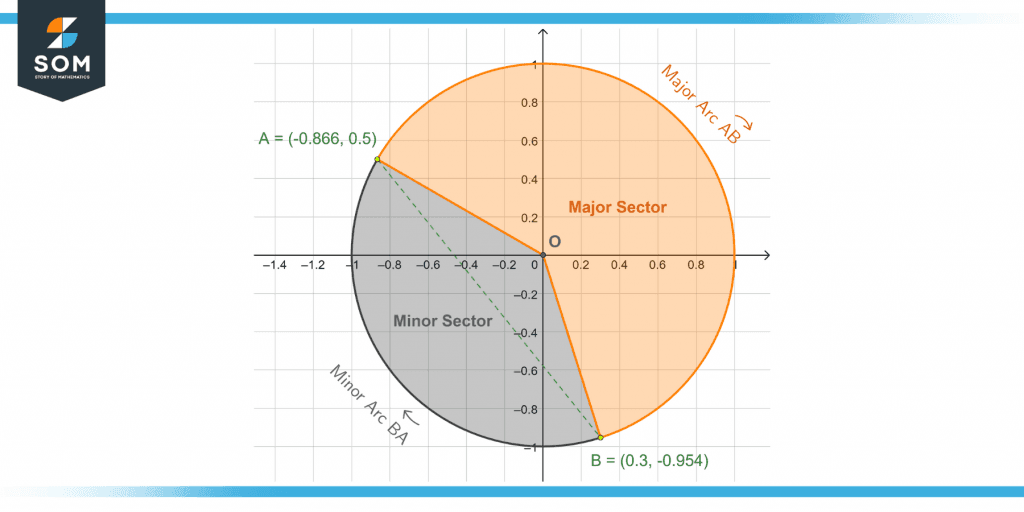
Figure 5 – The major and minor arcs and sectors of the unit circle from the first Example.
Point in the second quadrant: (0.3. -0.954)
Point in the fourth quadrant: (-0.866, 0.5)
Traversing the circle clockwise from A to B, it turns out to be a major arc.
Example 2
Consider the same circle from Example 1. Now find the arc in the anti-clockwise direction between the points y = -0.8 in the third quadrant and x = 0.6 in the first quadrant. Is this arc major or minor?
Solution
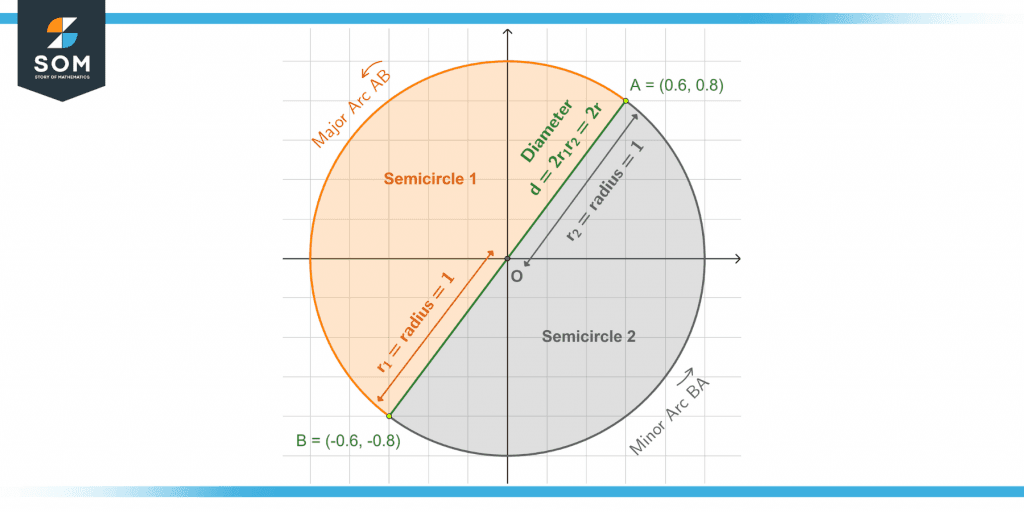
Figure 6 – Points A and B from the second example result in major and minor arcs of equal length and hence, semicircles.
Point in the third quadrant: (-0.6. -0.8)
Point in the first quadrant: (0.6, 0.8)
Since the result is a pair of equivalent semicircles, there is no distinction between the major and minor arcs.
Example 3
Find the areas of the minor sectors and segments defined by the arcs in Examples 1 and 2. Further, what is the major arc’s length in Example 1?
Solution
First, we consider the results of Example 2 as they involve semicircles. We can see that:
area of the first sector = area of the first segment = area of the first semicircle
area of the second sector = area of the second segment = area of the second semicircle
area of the first semicircle = area of the second semicircle
The area of a semicircle must be half the area of the circle, so we have the following:
area of circle = Acircle = $\pi$r2 = 3.14159 x (1)2 = 3.14159 square units
area of each semicircle = 0.5 x Acircle = 0.5(3.14159) = 1.57079 square units
We can see that the sum of the two semicircles’ area adds to the area of the full circle, except for some rounding errors.
Now, consider the case in Example 1. The formulae for the areas of sector and segments use the angle between the two bounding radii (θ), which we do not have.
Finding the Angle Between the Bounding Radii
To find it, we must find the length of the segment AB. Using the distance formula (xa = -0.866, xb = 0.3, ya = 0.5, yb = -0.954):
\[ \mathsf{|\overline{AB}| = \sqrt{(x_a-x_b)^2+(y_a-y_b)^2} = \sqrt{3.474} = 1.864} \]
Now we have the length of three sides of the triangle OAB, such that AB = 1.864 and OA = OB = 1. We will use the law of cosines. Given three sides, a, b, and c, of a triangle, we can find the angle $\theta$ between a and b:
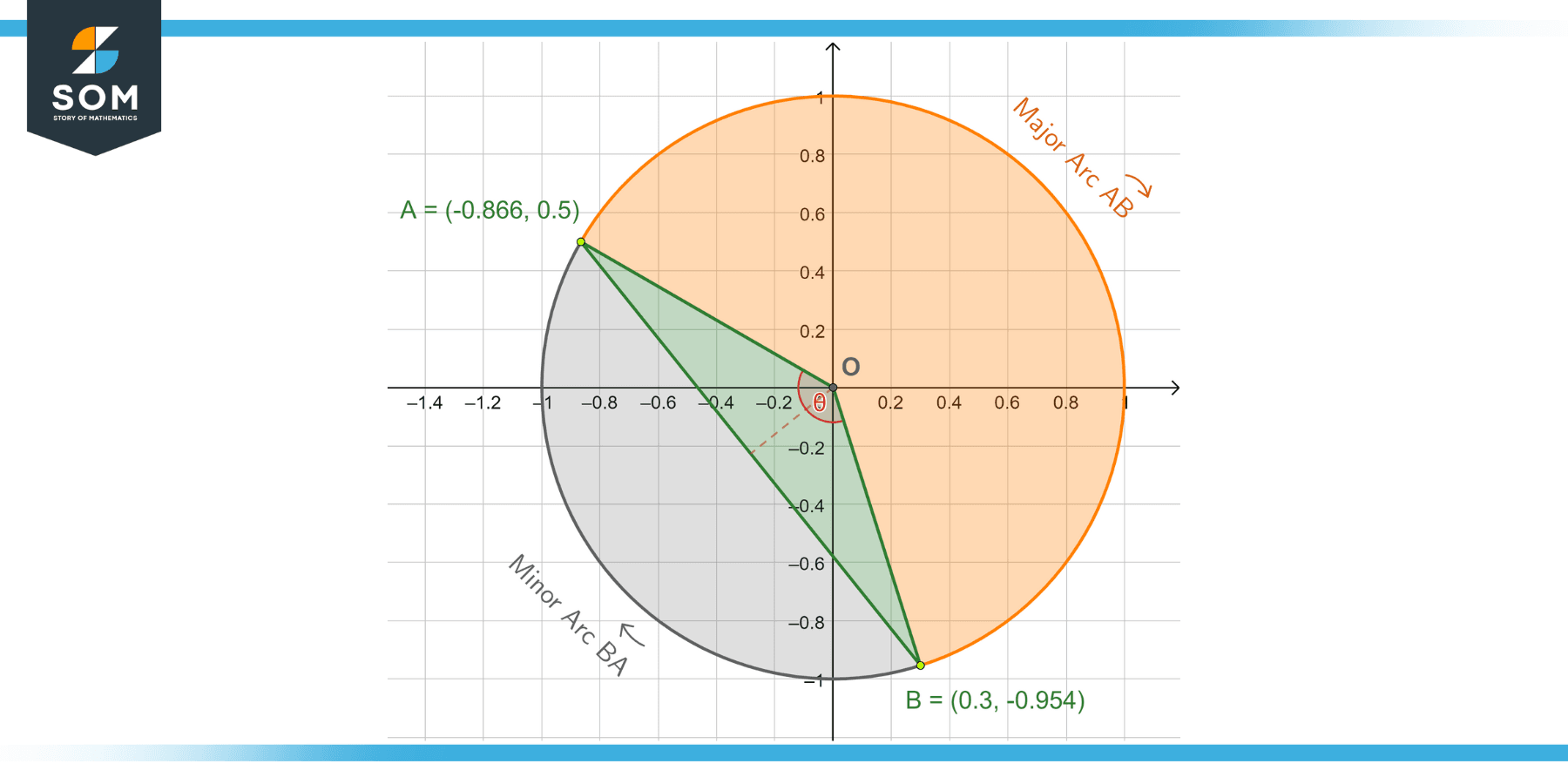
Figure 7 – Finding the angle θ between the bounding radii of the minor segment OAB.
\[ \mathsf{\theta = \cos^{-1}\left(\frac{a^2+b^2-c^2}{2ab}\right)} \]
In our case, a = OA = 1, b = OB = 1, and c = AB = 1.864. Plugging these in:
\[ \mathsf{\theta = \cos^{-1}\left( \frac{-1.4745}{2} \right) = 137.497^\circ = 137.5^\circ} \]
Length of the Major Arc and Area of the Minor Sector and Segment OAB
Given that the minor arc angle is 137.5$^\circ$, the major arc’s angle must be 360 – 137.5 = 222.5$^\circ$. Therefore, with r = 1, the length of the major arc is:
l = r x $\displaystyle\mathsf{\frac{\theta \times \pi}{180}}$
l = 1 x (222.5 x 3.14159) / 180 = 3.8834 units
Now, plugging in $\theta$ = 137.5$^\circ$ and r = 1 into the formulae for sector and segment areas (after converting from degrees to radians), we get:
area of sector OAB = 1.2 square units
area of segment AB = 0.862 square units
All images/mathematical drawings were created with GeoGebra.