JUMP TO TOPIC
Major Axis|Definition & Meaning
Definition of Major Axis
Major axis is the longer axis of the ellipse that connects the two farthest points of its perimeter while passing through its center.
When we talk from the perspective of geometry, an ellipse is a type of standard shape which is two-dimensional and which can be described by its two axes. The elliptical shape is generally created when a plane intersects a conic at a tilted angle with the base of the cone. All ellipses have two axes.
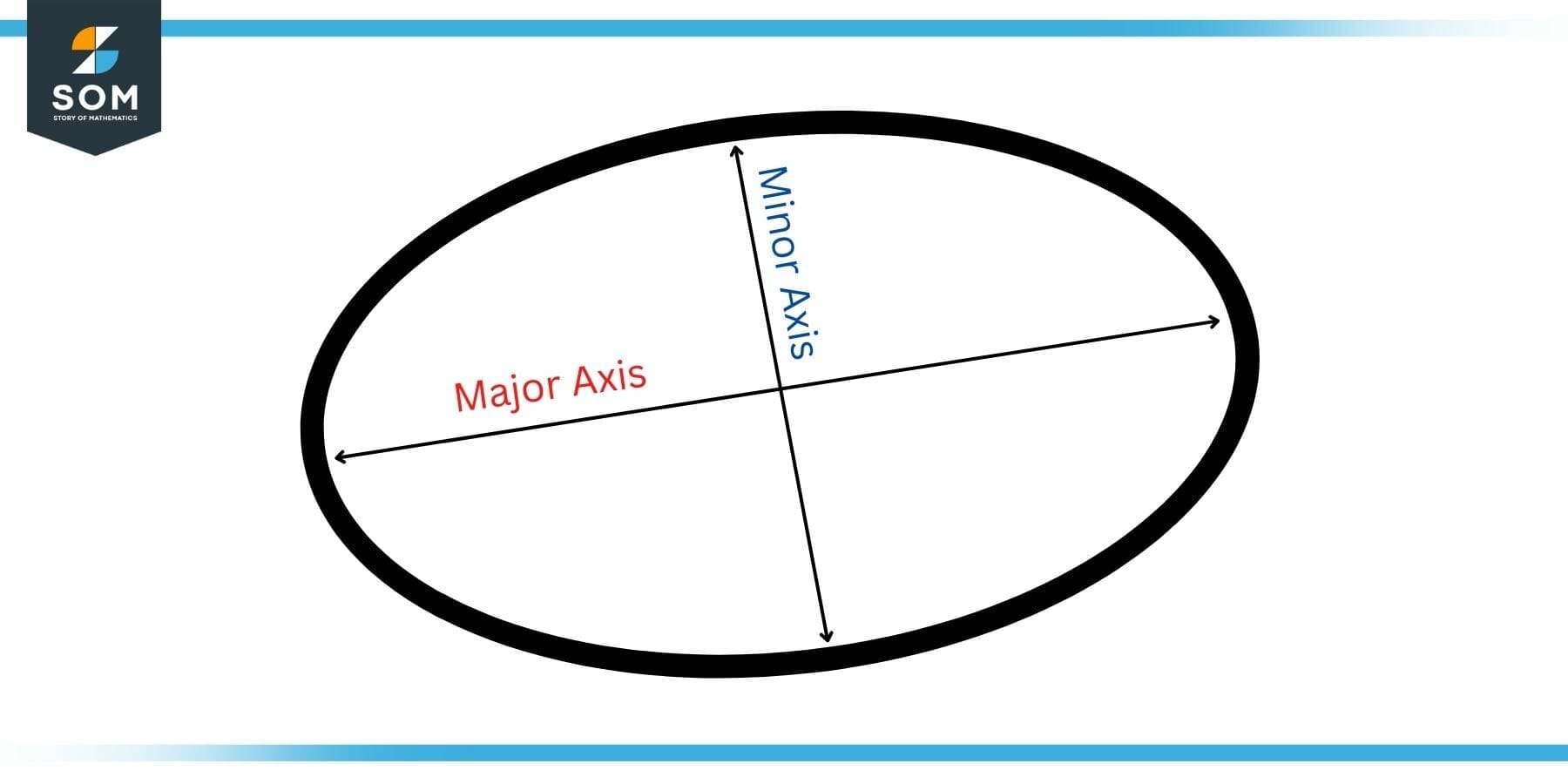
Figure 1: Axes of an Ellipse
The major axis is the ellipse’s longest diameter (denoted as ‘a’ by convention), which goes through the ellipse’s center from one end to the other. The minor axis (denoted as ‘b’ by convention) is the ellipse’s smallest diameter, passing through the center at its narrowest point.
Explanation of Major Axis of Ellipse
A line segment connecting the elliptical shape’s farther vertices is termed a major axis. It can also be defined as the longest one of the two diameters of the ellipse.
Let us say that we have an ellipse with the center at C, as shown in figure 2. Now we can see the four vertices of the ellipse at points marked as A, A’, B, and B.’
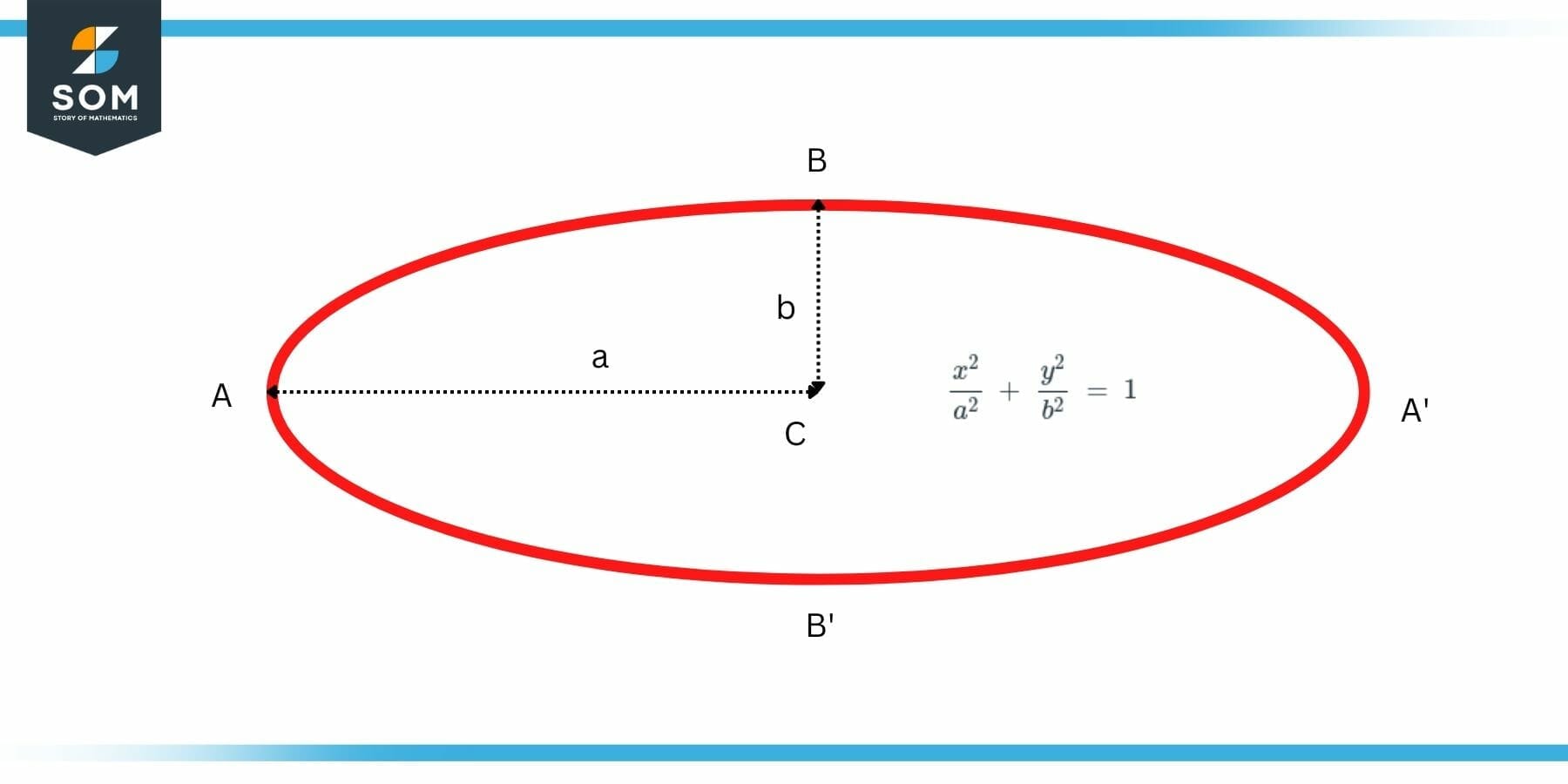
Figure 2: Mathematical Form of Major Axis of an Ellipse
The line segments joining the opposite vertices and passing through center C are called the axes of this ellipse. The line segment BB’ joining the closest vertices, that is B and B’, is known as the minor axis of the ellipse. While the line segment AA’ joining the farthest vertices, that is A and A’, is termed as the major axis of the ellipse.
In the above diagram, the distance of the farthest vertices, that is, A and A’, from the center C is equal to ‘a’. Therefore, the distance from A to A’ will be a + a = 2a which is the length of the line segment AA’ and the length of the major axis.
Mathematical Form of Major Axis of an Ellipse
Mathematically, the equation of an ellipse can be written in two-dimensional space in the following standard form:
\[ \dfrac{x^2}{a^2} \ + \ \dfrac{y^2}{b^2} \ = \ 1 \]
In the above formula, the two dimensional Cartesian coordinates have been represented by x and y. ‘a’ and ‘b’ defines the distances between the center of the ellipse and its vertices. Since the ellipse may be oriented in any direction or at any rotation angle, we may not explicitly say which one of these lengths is a part of the minor axis or major axis.
It is a common practice first to solve the equation given in the question such that it resembles the standard form (as given in the equation above). Once we have this standard form, we can evaluate the values of a and b. After that, we can compare which one of these is a larger distance. Suppose if a > b, the length of the major axis will be 2a, and the length of the minor axis will be 2b.
Similarly, if a < b, then the length of the minor axis will be 2a, and the length of the major axis will be 2b. We can see this process in further detail under the numerical problems section of this article.
Examples of Major Axis of Ellipse
There are many real-life examples of the major axis of an ellipse. The following paragraphs detail only two of such examples.
The first example is the one of an American football. The ball, as shown in figure 3, is elliptical. We can mathematically define its dimensions by specifying the two distances of its major and minor axes. The distance of the two notches, as shown in the figure, represents the major axis, while the diameter of the ball right in the middle section represents its minor axis length.
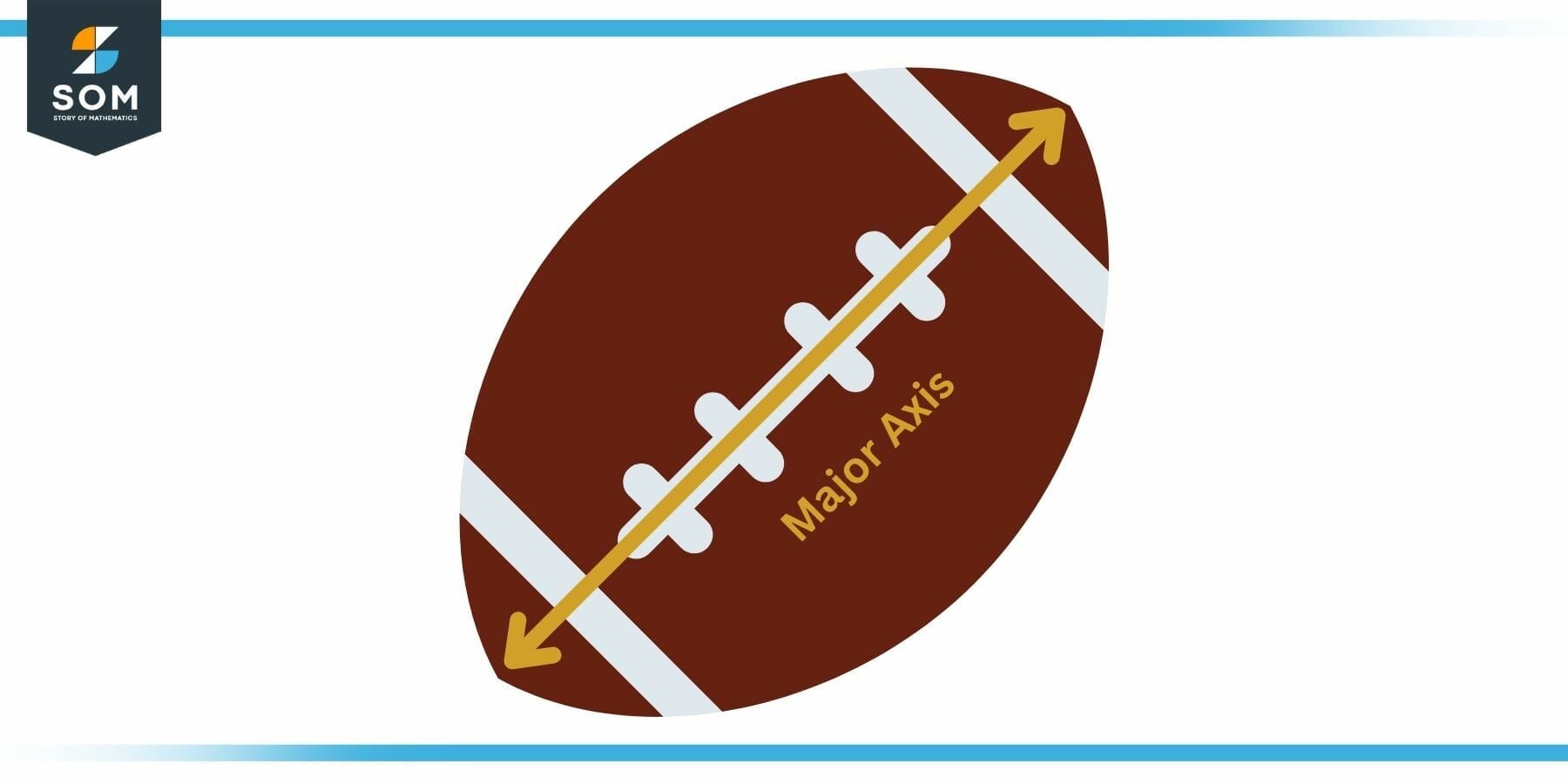
Figure 3: Football Example of Major Axis of an Ellipse
The second example is also a very familiar one: the solar system. The following figure shows the path of our home planet around the Sun. We know that all the planets circulating the Sun follow an elliptical path. This elliptical path means that during the whole year-long cycle of Earth, our globe is not at a constant distance from the Sun. Rather it keeps changing, and this change creates seasons on Earth. The major axis of the Earth’s orbit is marked in the following figure.
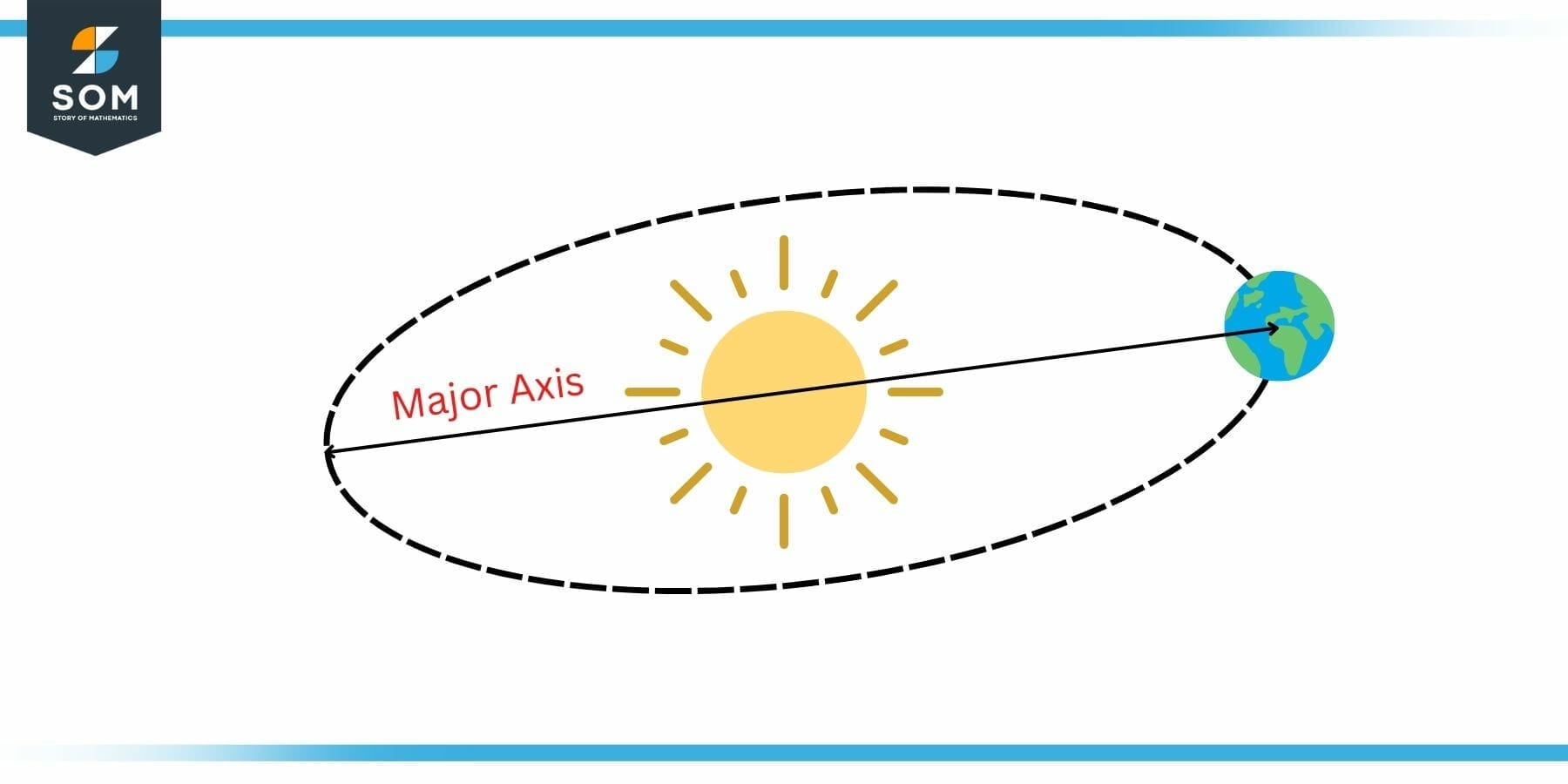
Figure 4: Solar System Example of Major Axis of an Ellipse
Numerical Examples of Major Axis
Example 1
Given the following equation of an ellipse, find both (minor as well as major) axes of this ellipse.
9x$\mathsf{^2}$ + 4y$\mathsf{^2}$ = 36
Solution
Given:
9x$\mathsf{^2}$ + 4y$\mathsf{^2}$ = 36
Converting into standard form:
\[ \dfrac{ 9 x^{ 2 } }{ 36 } \ + \ \dfrac{ 4 y^{ 2 } }{ 36 } \ = \ \dfrac{ 36 }{ 36 } \]
\[ \dfrac{ x^{ 2 } }{ 4 } \ + \ \dfrac{ y^{ 2 } }{ 9 } \ = \ 1 \]
Comparing with the standard form, we have the following:
a$\mathsf{^2}$ = 4
a = 2
b$\mathsf{^2}$ = 9
b = 3
Comparing ‘a’ and ‘b,’ since b > a, ‘b’ is the part of the major axis while ‘a’ is the part of the minor axis.
Length of Major Axis = 2b = 2(3) = 6
Length of Minor Axis = 2a = 2(2) = 4
Example 2
Given the following equation of an ellipse, find both (minor as well as major) axes of this ellipse.
16x$\mathsf{^2}$+ 25y$\mathsf{^2}$ = 400
Solution
Given:
16x$\mathsf{^2}$+ 25y$\mathsf{^2}$ = 400
Converting in standard form:
\[ \dfrac{ 16 x^{ 2 } }{ 400 } \ + \ \dfrac{ 25 y^{ 2 } }{ 400 } \ = \ \dfrac{ 400 }{ 400 } \]
\[ \dfrac{ x^{ 2 } }{ 25 } \ + \ \dfrac{ y^{ 2 } }{ 16 } \ = \ 1 \]
Comparing with the standard form, we have the following:
a$\mathsf{^2}$ = 25
a = 5
b$\mathsf{^2}$ = 16
b = 4
Comparing ‘a’ and ‘b,’ since a > b, ‘a’ is the part of the major axis while ‘b’ is the part of the minor axis.
Length of Major Axis = 2a = 2(5) = 10
Length of Minor Axis = 2b = 2(4) = 8
All images/mathematical drawings were created with GeoGebra.
