Mantissa|Definition & Meaning

The term “mantissa” can be found in the field of mathematics, specifically in the fields of computer science and engineering. Floating-point arithmetic, which is a way of representing real numbers in a computer, makes use of this fundamental concept, and it is essential to the process. 

The mantissa is a representation of the fractional part of a number. The relevance of the mantissa comes in the fact that it offers a means of representing extremely small or extremely big numbers in a form that is more condensed.

The fractional component of an integer’s logarithm with respect to base 10 is referred to as the mantissa of the number in mathematical parlance. When we write a number in scientific notation, the part of the number that corresponds to the decimal system is called the mantissa.

For instance, the number 256987 can be represented in scientific notation as 2.56987 multiplied by 10⁵, and the mantissa value in this instance would be 2.56987.

In a computer system, the mantissa is frequently kept as a binary number. This allows the value of the mantissa to be represented by a fixed number of bits.

The precision of the floating-point representation can be thought of as the number of bits that are utilized in order to represent the mantissa. The representation will be more accurate if more bits are utilized to represent the mantissa than are now being used.

Mantissa in Computer

The component of a number that comprises the significant digits is called the mantissa of the number. The portion of a floating-point number that comprises the significant digits is referred to as the mantissa in the field of computer science.

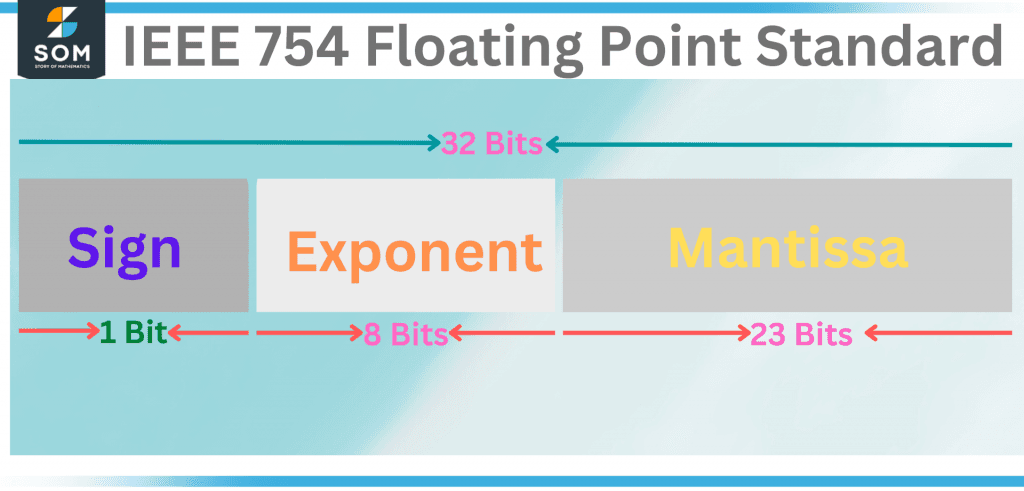
Figure 1 – IEEE Floating Point Standard

In the representation of the mantissa as a fraction, the position of the decimal point is considered to be to the right of the digit with the highest significance.

The Key Differences Between Standard Notation and Scientific Notation

A method of expressing numbers that are either too large or too little to be conveniently represented in decimal form is known as scientific notation. This method of notation is also known as scientific form, standard index form, or standard form in the UK.

If the exponent of ten is a negative number, shift the decimal point to the left; if the exponent of ten is a positive integer, move the decimal point to the right. This will convert the number from scientific notation to standard form (if the exponent is positive). You need to move the point the same number of times that the exponent tells you to.

One example of scientific notation is the expression “1.545 x 10⁵,” which is merely a variation on the way the number 1,545,00 is written in conventional notation. The conventional technique of writing numbers is referred to as standard notation.

Figure 2 – Graphical Depiction of Scientific Notation

The exponent, which has a base of 10, is determined by the number of digits that are tallied. If you count to the left, the exponent will be positive; if you count to the right, it will be negative.

In addition, there are specific guidelines that must be adhered to in order to execute arithmetic operations with numbers that are written in scientific notation and to guarantee that the number is displayed in the appropriate format.

What Is Exponent and Mantissa?

Both a mantissa and an exponent are acceptable ways to express extremely large numbers when working with the decimal system. In 2.5 x 10⁶, 10⁶ = 1000000 is the exponent, 2.5 is the mantissa, and the result of multiplying the two is 2500000. Two different kinds of exponents can be placed on the principal digits of the mantissa.

Figure 3 – Exponent and Mantissa of a Number

The first kind of exponent specifies the order in which the decimal point should be placed. The second kind of exponent specifies the order in which the decimal points should be placed. Using the same process, it is also possible to convert a binary number to the value one.

Explanation With Example

The mantissa is a fraction of a common logarithm, often known as the logarithm, with a base of 10, and it is used to indicate the digits of the provided number rather than the magnitude of the number itself. Therefore, log₁₀ (20) = 1.3010 and log₁₀(200)  = 2.3010 both have a mantissa value of 0.3010, as shown here.

It is important to take note that the mantissa of log₁₀(0.2) = 0.6990 is also 0.3010. This is because the value of the fractional portion must consistently fall between 0 and 1. Because 0.6990 is equal to -1 plus 0.3010 in this instance, the integer component is -1, while the fractional component is 0.3010.

Let us see another example where the value 847.13 x 10¹ is written in scientific notation (with a mantissa of 847.13), but it is not written in normal scientific notation, which would be 8.4713103.

It is also important to note that the exponent may be negative for values with tiny magnitudes (absolute values that are less than 1), indicating the number of times the mantissa would need to be divided by 10 in order to obtain the “regular value.” This is something that should be kept in mind.

For instance, the “regular value” of 0.00002914 would be similar to the value of 2.914 x 10^-5. A hint is that in order to solve this problem, we need to describe what a mantissa is.

It is important for us to understand that the part of a number that comes after the decimal point is called the mantissa in decimal numbers and that in scientific notation, the mantissa and the exponent are the two significant components of a number. Mantissa can be represented in decimal numerals as well as in scientific notation, as we will see now.

In a decimal number, the component of a number that comes after a decimal point is referred to as the mantissa. Let’s look at an example: for the value 6.745, the integer component is 6, and the mantissa is:

⇒ 0.745

In scientific notation, on the other hand, we know that the mantissa is the first part, and the power of 10 that the mantissa is multiplied by is the exponent. Notice that the value of the exponent corresponds to the number of times you must multiply the mantissa by 10 to get a regular number.

Let’s take a look at an example for this case: the scientific notation looks like this: 5.367 x 10³. The mantissa of this value is: 

⇒ 5.367

Note: Keep this difference in mind to avoid confusion later on. The part of a number that comes after the decimal point is the mantissa for decimal numbers, but in scientific notation, the mantissa is the complete decimal part that’s not a power of 10.

Conclusion

The mantissa is a fundamental idea in both mathematics and computer science, and it is applicable in a wide variety of other disciplines as well, including engineering, physics, and even finance. A compact representation of real numbers is provided by the mantissa, which is very helpful in computer systems with a limited amount of memory to work with.

The mantissa makes it possible to construct mathematical models and algorithms that, in the absence of this, would be impossible to carry out. It does this by enabling the representation of real numbers in a form that takes up less space.

Example of Mantissa

Find the mantissa of log₁₀(25).

Solution

log₁₀(25) = 1.397940

= 1 + 0.397940

The integral portion of the expression is 1, while the decimal or fractional portion is 0.397940. Therefore, the characteristic for the number log₁₀(25) is 1, and the mantissa is 0.397940.

All images were created with GeoGebra.

Major Axis Definition < Glossary Index > Markup Definition