Maximum|Definition & Meaning

Conceptual Overview 

Maximum of Function

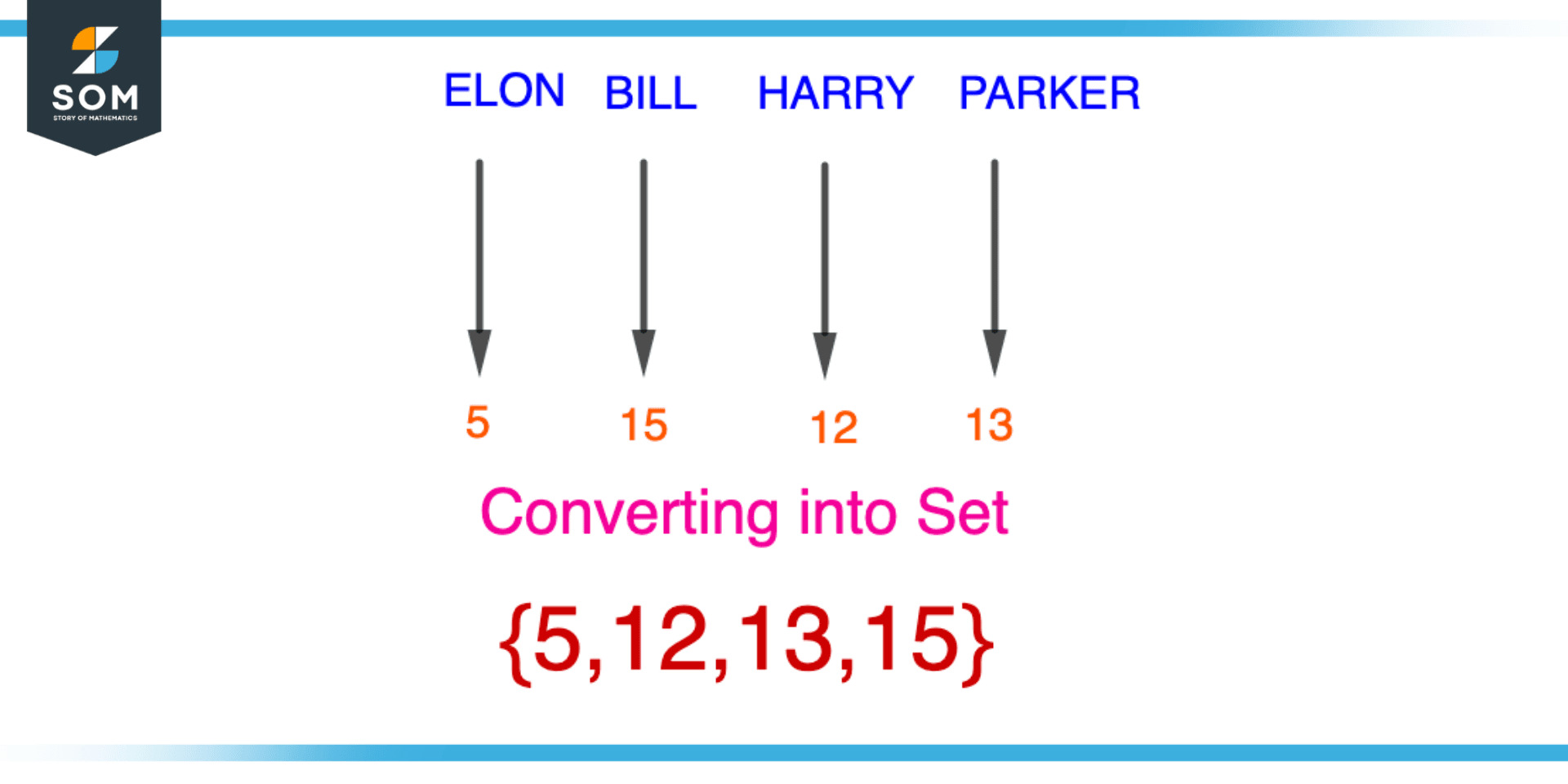
Figure 1 – Maximum Age among four persons

A function can be maximized by finding the highest possible value with the concept of maximum. Using an input (called the independent variable) and a set of instructions, a function produces an output (called the dependent variable). A function is often represented by a graph, and its inputs and outputs are linked by a mathematical rule.

Consider an example in which the age of the 4 persons are given Elon is 5 years old, Bill is 15 years old, Harry is 12 years old and Parker is 13 years old we will convert the ages into set form {5,12,13,15}, when we try to find the maximum of the set i.e. max{5,12,13,15}=15. So the maximum age among the persons will be 15.

Steps to Find Maximum of a Function

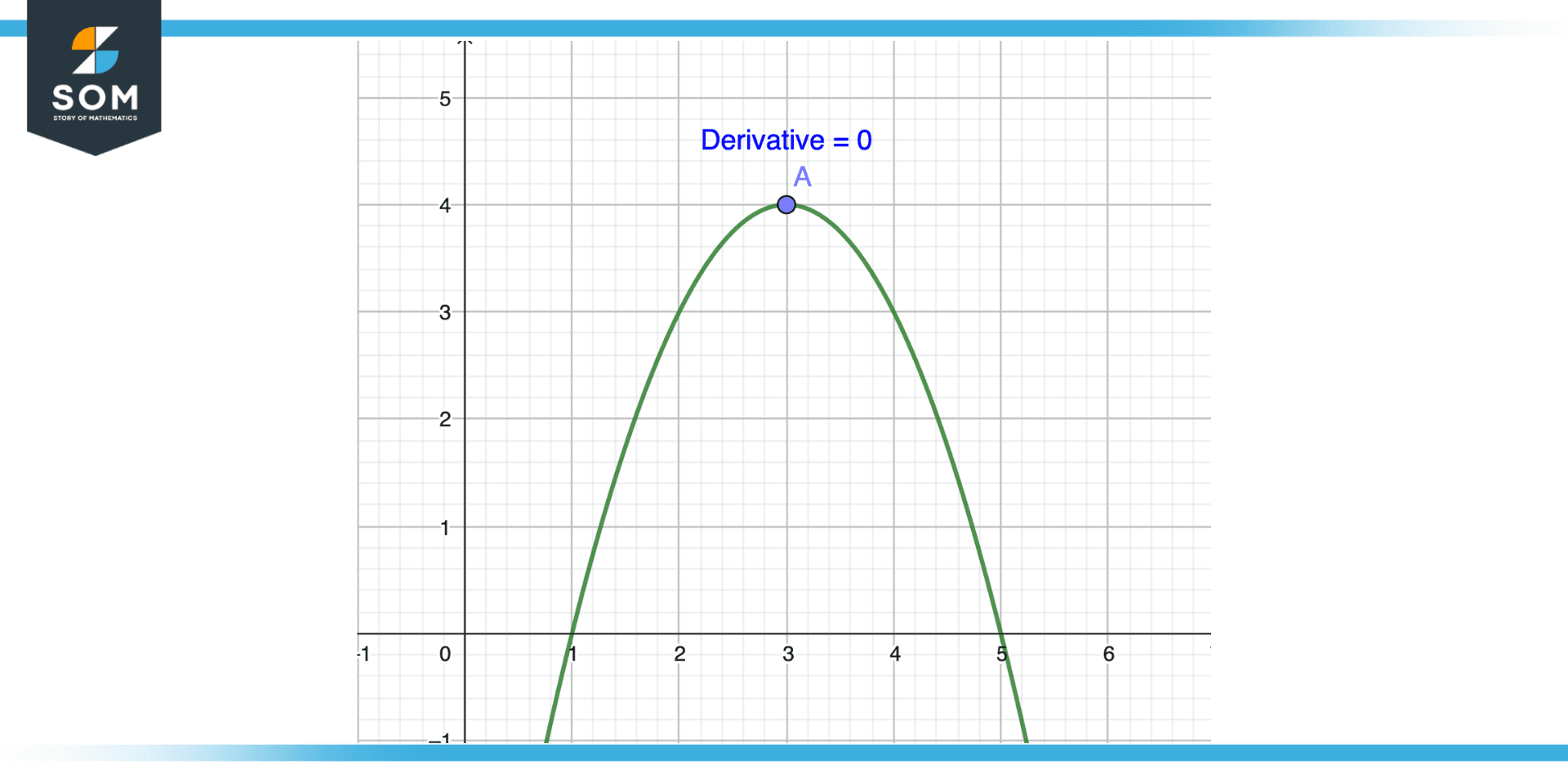
Figure 2 – Maximum of a function

We must first determine the domain of the function in order to find its maximum value. An independent variable’s domain consists of all possible values it can assume. Time, for instance, might be the independent variable, and all real numbers over or equal to zero might be its domain.

We can determine the maximum value in a function by taking its derivative and setting it to zero. Once we determine the domain, we can calculate the maximum value. An input changes and the output changes accordingly, so the derivative measures how the output changes. By setting the derivative equal to zero, we are finding the points at which the output of the function is not changing, which means that it is either at a maximum or a minimum value.

Alternate Method to Find the Maximum of a Function

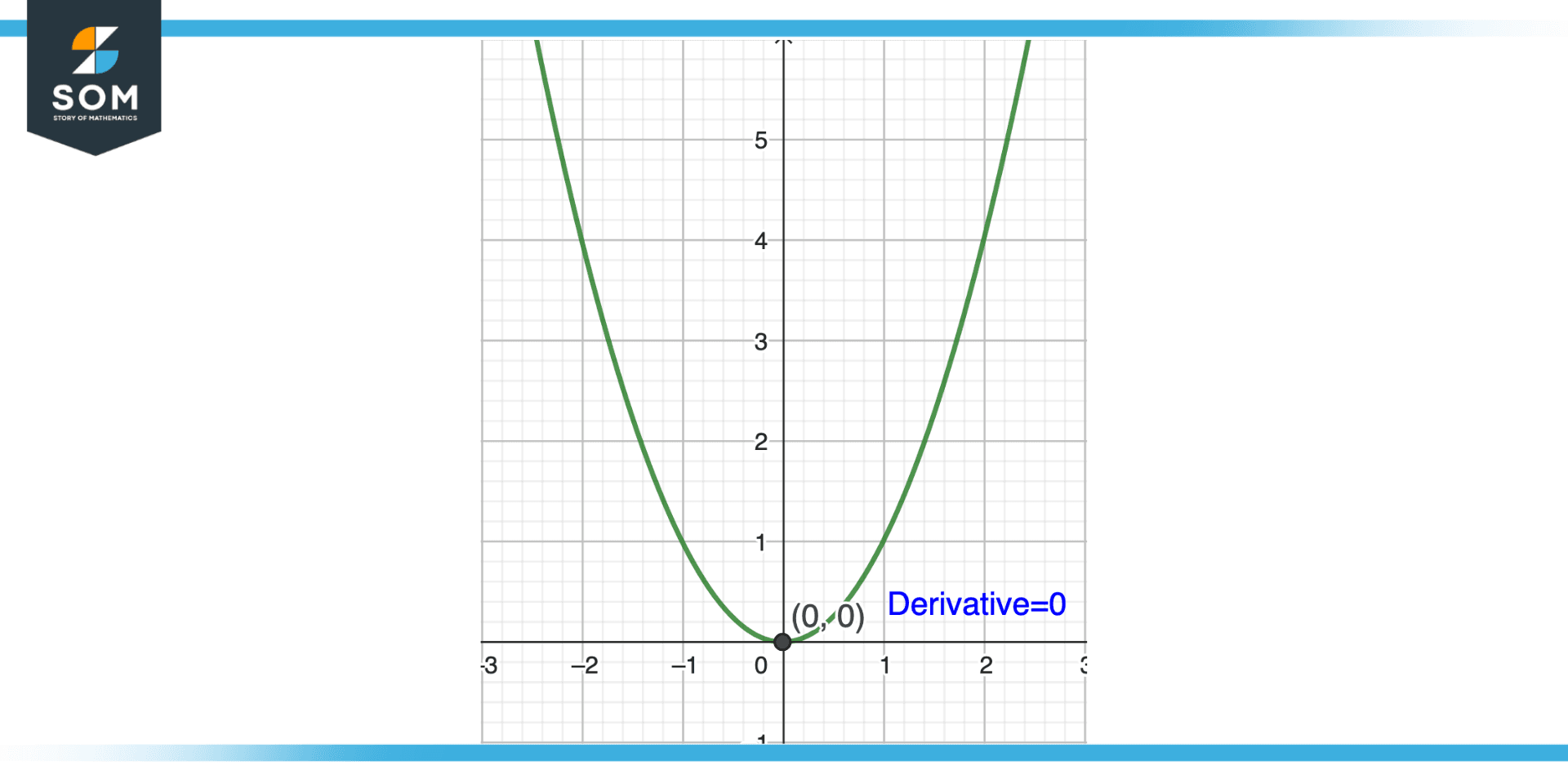
Figure 3 – Alternate method to find maximum of function

However, we can also look at the function’s graph to determine the maximum value. The highest value is found at the apex of the upward-opening parabola that forms the graph in the case of $f(x) = x^{2}$. The coordinates of the parabola’s vertex must be discovered in order to determine this maximum value. By averaging the x-coordinates of the two sites where the derivative equals zero, the vertex—the point at which the parabola changes direction—can be identified. Since there are no points in this scenario where the derivative equals zero, the vertex is at (0, 0).

Properties of Maximum

There are several properties that are often associated with the concept of maximum in mathematics:

Uniqueness

Most of the time, a particular set or range only contains one maximum value. For instance, there will typically be just one value that is the highest if we are looking for the greatest value of a function inside a particular range.

Existence

 There must be at least one maximum value for a given set or range. This is because there must be at least one value in the set or range for there to be a maximum, and the maximum value is just the highest value within the set or range.

Monotonicity

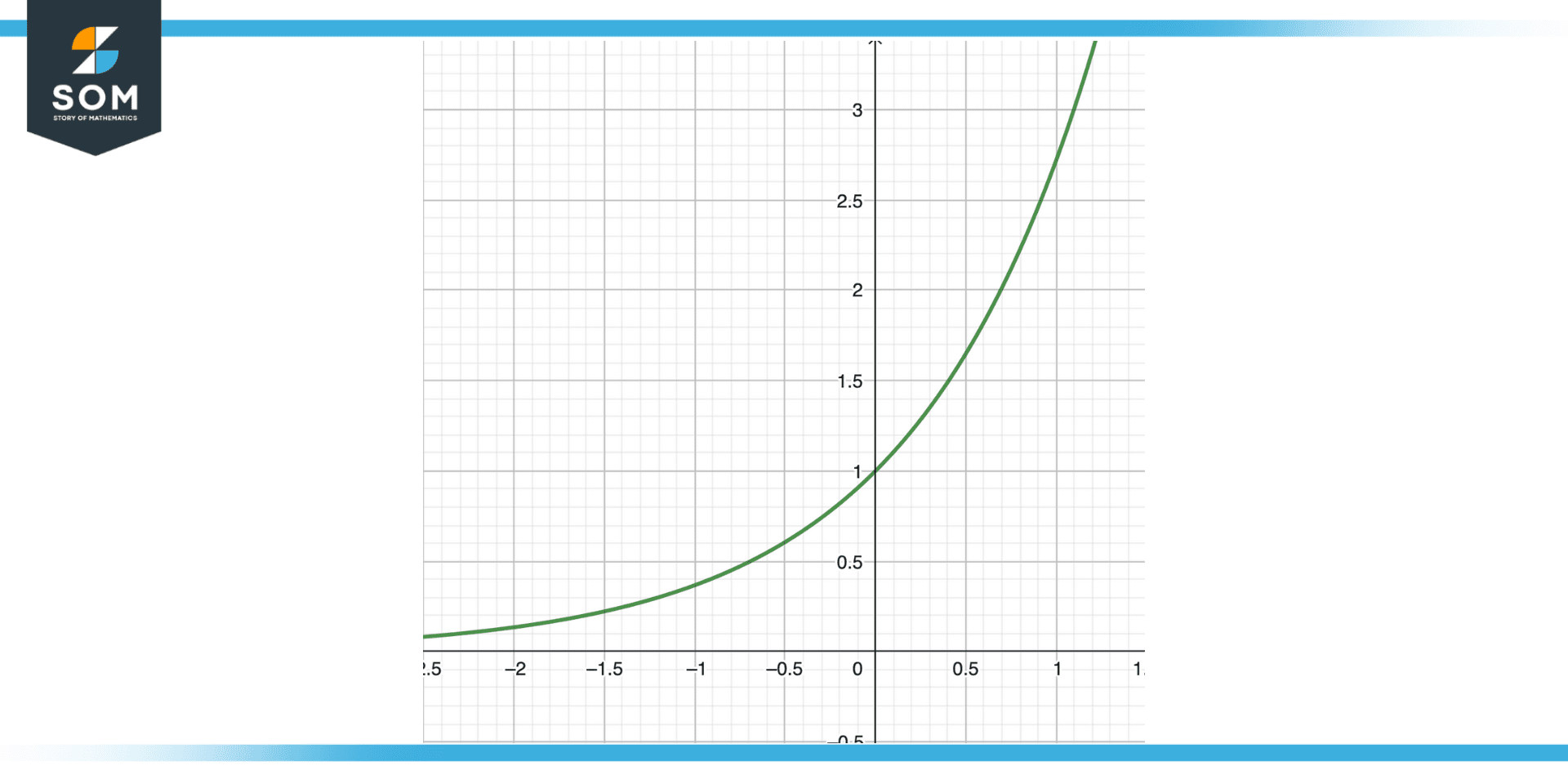
Figure 4 –  Monotonicity of function

As the input values rise, the maximum value of a function either rises or stays the same. This means that if we are looking for the maximum value of a function, we may frequently focus our search by only taking into account input values greater than the maximum value at the moment.

Continuity

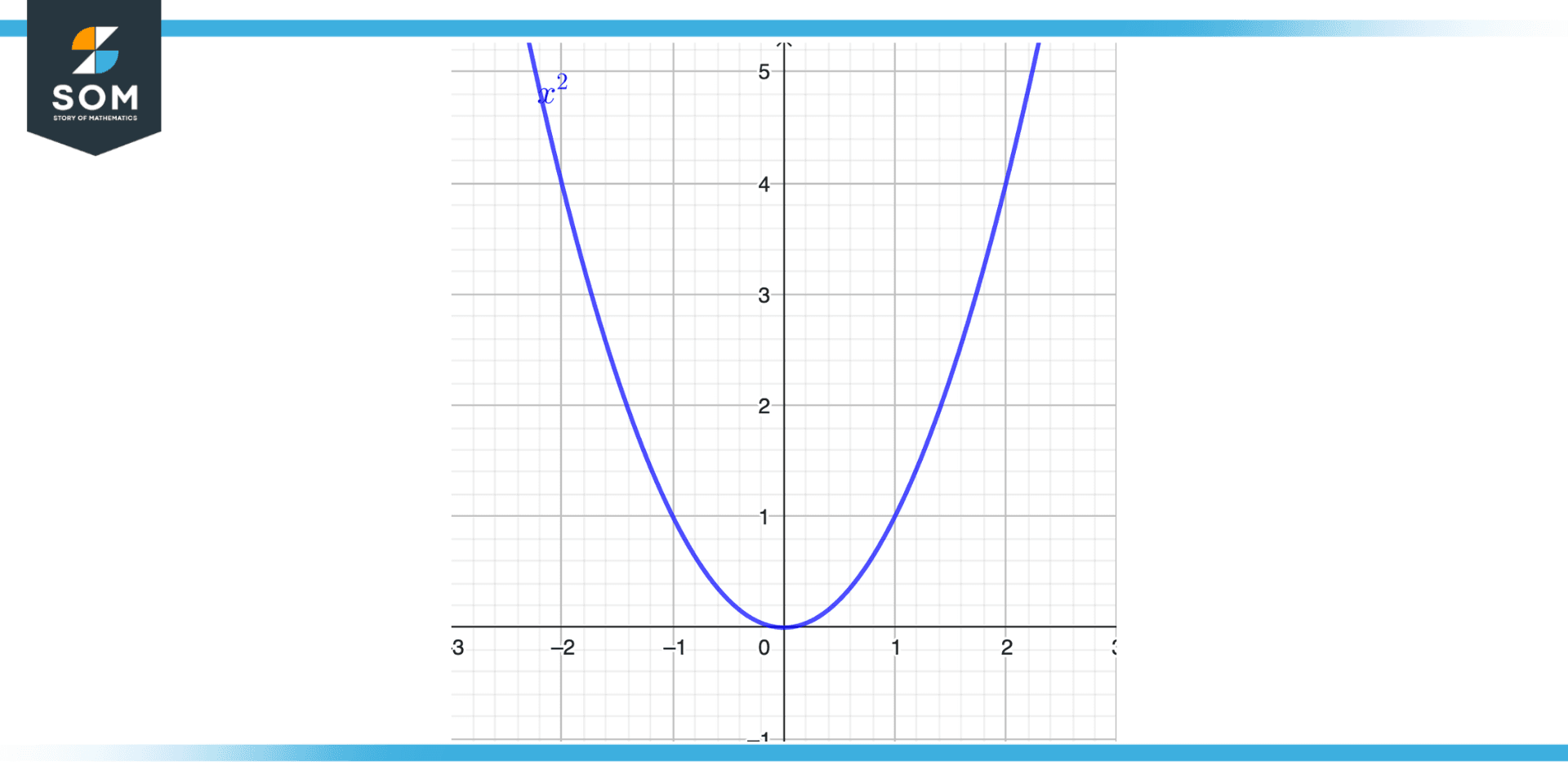
Figure 5 –  Continuity of function

A function’s maximum value is often a continuous point included inside the set or range. This indicates that the function’s value won’t drastically change at its maximum point.

Global vs. Local Maximum

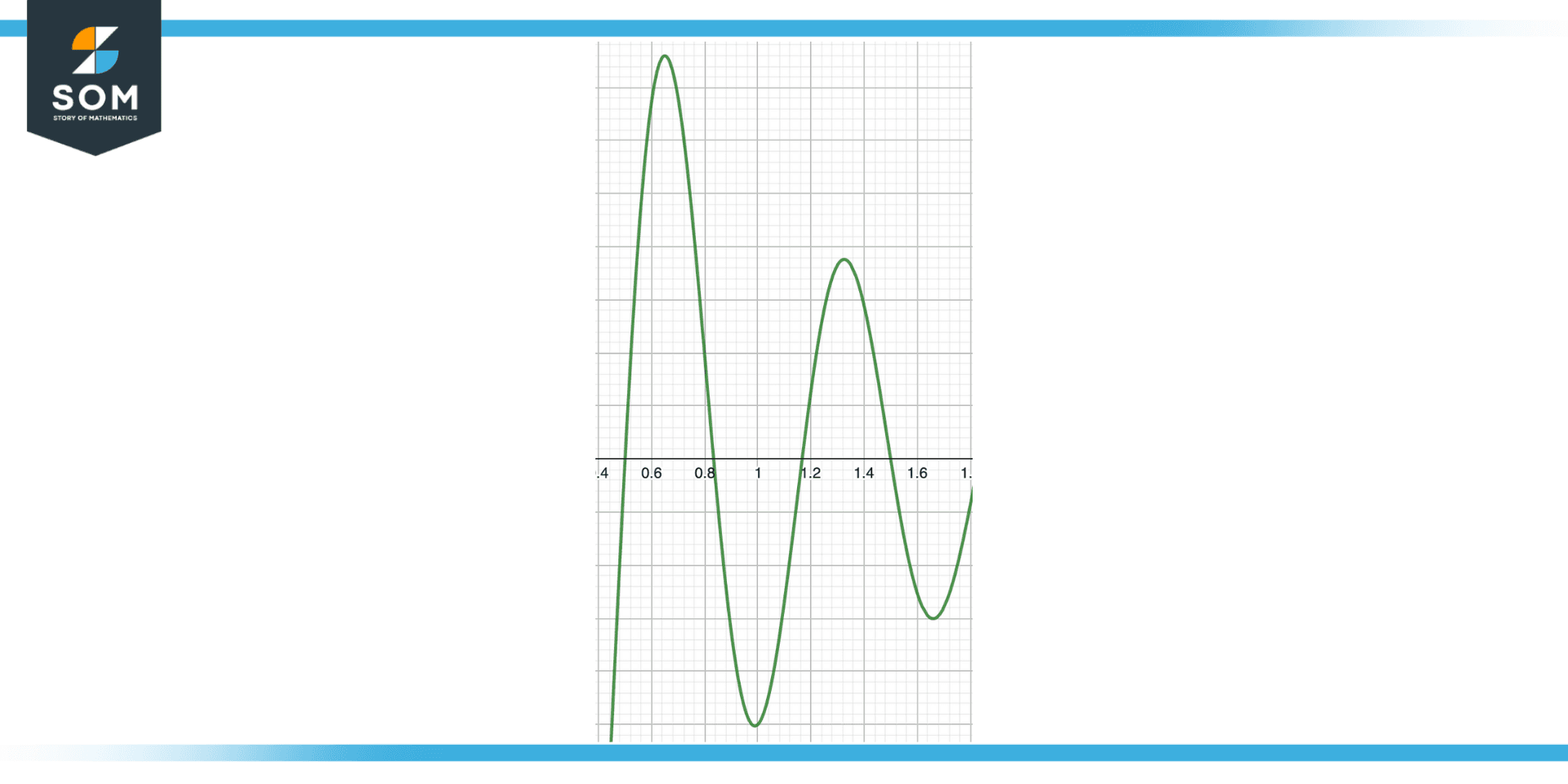
Figure 6 –  Global vs Local Maxima

The greatest value inside the entire set or range is referred to as a global maximum, while the highest value within a smaller subset of the set or range is known as a local maximum.

Boundaries

 At the edges of the set or range, a function’s maximum value may occur. For instance, if we are attempting to determine a function’s maximum value between [0, 1], the greatest value may occur at either x = 0 or x = 1.

Illustration of Maximum with Example

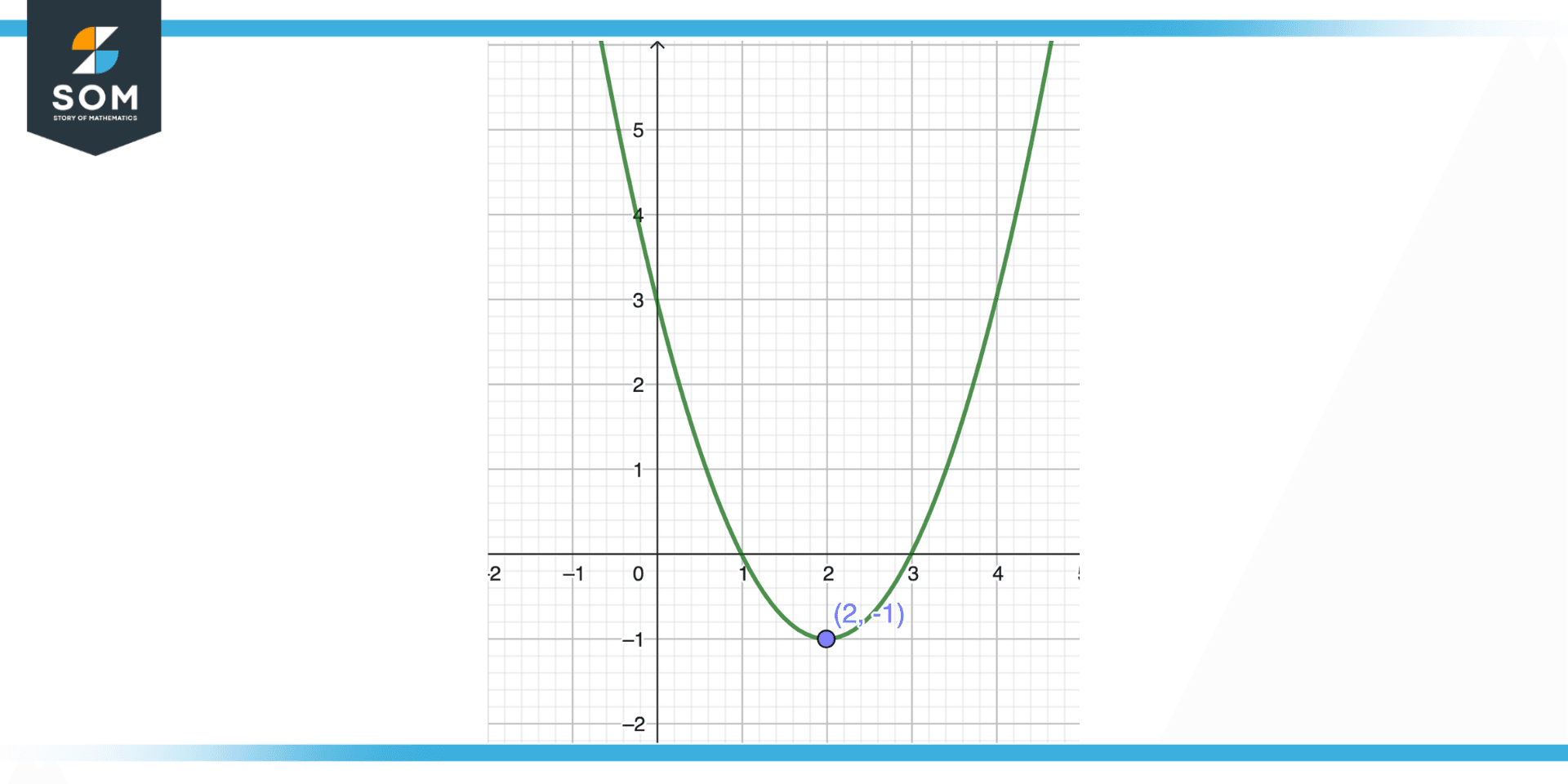
Figure 7 – Example of Maximum of a function

Here is an example of how the concept of maximum might be used in mathematics:

Suppose we have a function $f(x) = x^{2}-4x + 3$. We want to find the maximum value of this function. To do this, we can take the derivative of the function and set it equal to zero:

$f'(x) = 2x-4 = 0$

Solving this equation for x gives us x = 2. This means that the maximum value of the function occurs when x = 2.

To find the maximum value of the function, we can then evaluate the function at x = 2:

$f(2) = 2^{2}-4(2) + 3 = 4-8 + 3 = -1$

Thus, the maximum value of the function is -1.

Alternatively, we could also find the maximum value of the function by looking at the graph of the function. The graph of f(x) is a parabola that opens upwards, and the maximum value occurs at the top of the parabola. To find this maximum value, we need to find the coordinates of the vertex of the parabola.

The vertex is the point at which the parabola changes direction, and it can be found by taking the average of the x-coordinates of the two points at which the derivative is equal to zero. In this case, there is only one point at which the derivative is equal to zero (x = 2), so the vertex is at (2,-1).

This example illustrates how the concept of maximum can be used in mathematics to find the highest possible value of a function or equation.

By taking the derivative of the function and setting it equal to zero, or by looking at the graph of the function and finding the coordinates of the vertex, we can determine the maximum value of the function and understand the limits and boundaries of the quantity that it represents.

All mathematical drawings and images were created with GeoGebra.

Matrix Definition < Glossary Index > Mean Definition