Minimum|Definition & Meaning

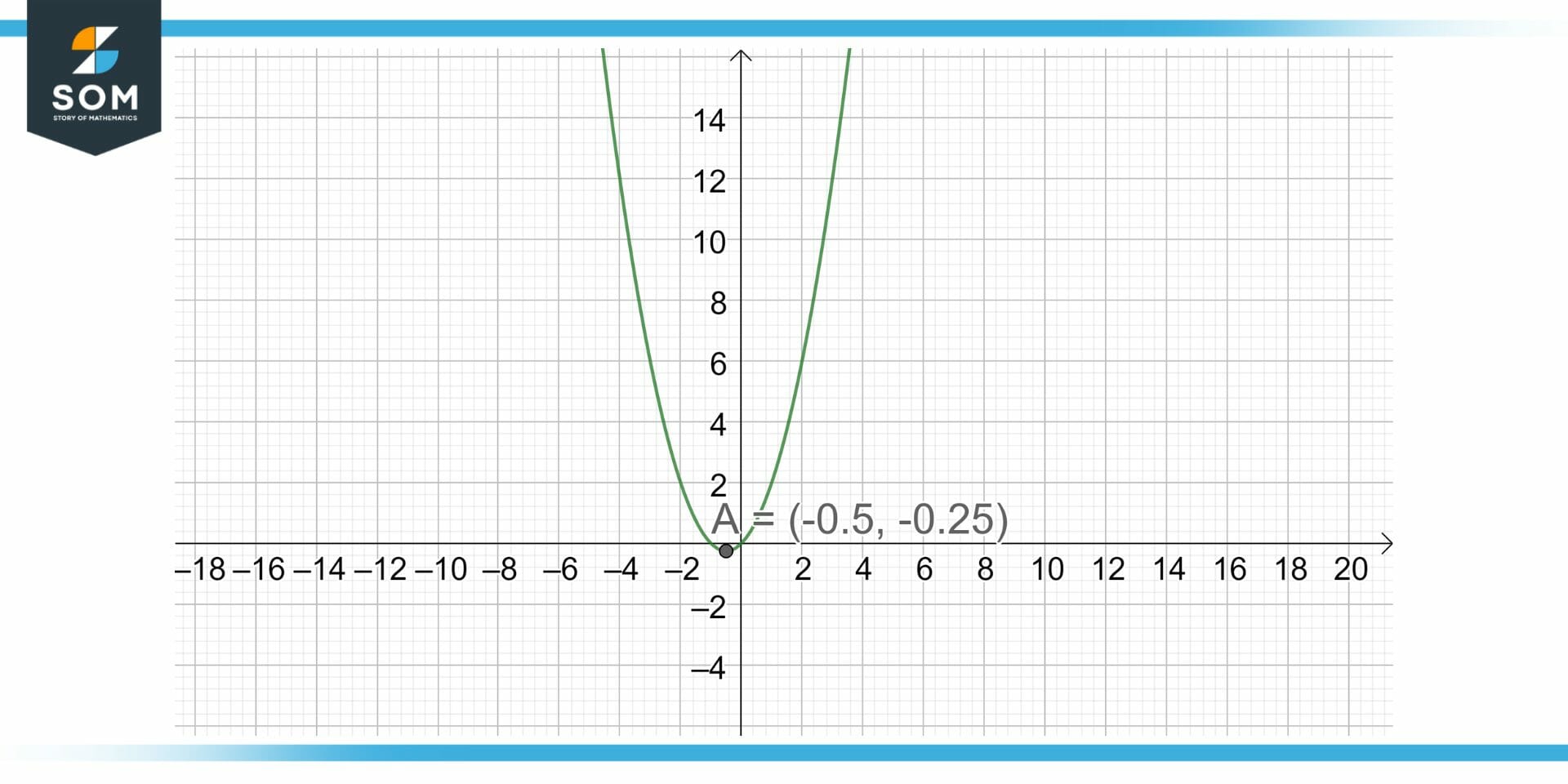
Figure 1: A Figure showing the minimum value of a function y = x$^2$ + x

The minimum is a part of the broader definition of extrema. The word “extrema” explains the upper and lower values of the given functions, which are possible within a set of constraints on that given function. Maximum or maxima here is similar to the minima, but it contains all the highest or largest values possible for the function to map or the set to contain. 

In a mathematical function, there are two types of minima: Local Minima and Absolute Minima. These two quantities explain the function depicted as a curve on a graph and help find the implicit meaning and trends of the functions. For a set, there is always a single minimum or maximum value, as it has a set of predefined values.

These predefined values cannot be altered or modified by any external factor.

Local Minimum and Global Minimum

Two types of minimums shape the function and explain its implicit meanings: Local minimum and global minimum. These two types of minimum help in clearly defining the properties of a function or a set and explain the trend that the set of values is depicting. 

A local minimum is the minimum value of a function for a specific interval of a function. The local minima are not necessarily the lowest value of all the function’s intervals, but they will be the lowest value for the interval where it occurs. Furthermore, we can also explain this as the lowest point concerning the nearby points on the graph is known as the Local Minimum.

The second type of minimum, the Global Minimum, is the lowest value of a function for the whole function. This means that no other point on the function is lower than the global minimum. This way, we can identify what is the lowest point that the function can reach throughout its whole interval.

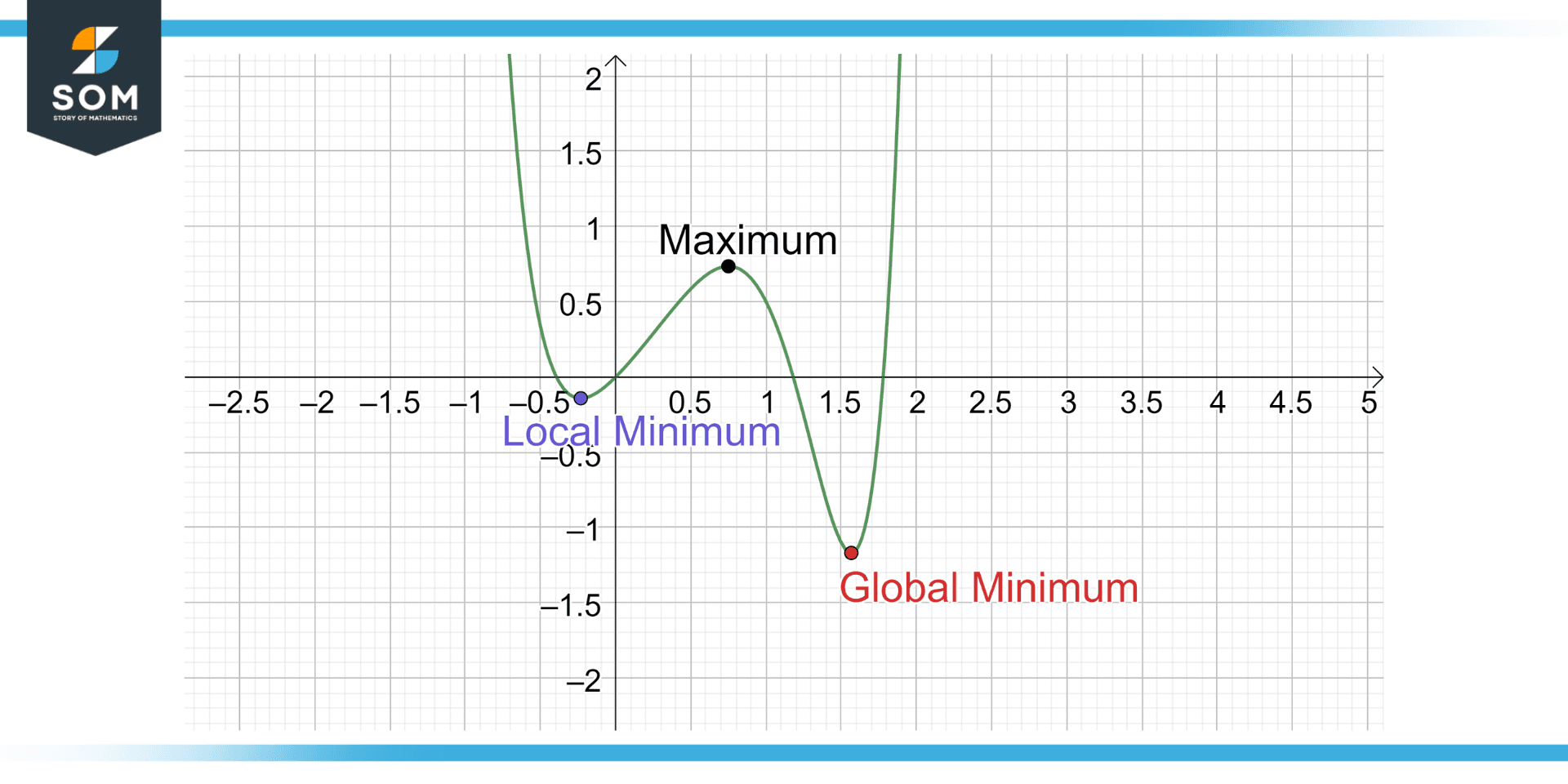
Figure 2: A curve showing different local minima and a global minimum.

Finding the Minimum Value of a Function

For a given function, it is a simple process to find the maxima or the minima value of a function. This extreme value is also known as a stationary value on the function. This means that the function is having a zero change in the function f(x) as the value of the x changes.

Thus, all we need to do is to find the derivative of the function given and equate it to zero. This way, the value of x in the function f(x) will be the stationary point, where there is no change in the value of f(x) for a minute change in x.

The following is the formula to find the stationary point for which we can find the minimum value of the function.

\[\frac{\mathrm{d}}{\mathrm{d}x}f(x) = 0\] 

So after finding the stationary point, all you need is to find the double derivative of the function f(x) and enter that stationary point x into the equation.

If the double derivative’s result is greater than zero, it will be a minimum point, and if the result is less than zero, it will be a maximum. This way, we can find the minimum of a function.

Applications and Significance of Maxima and Minima

Maxima and minima have innumerable applications in real-life problems and help in solving many different dilemmas that professionals face in their daily lives. An economist can utilize the maximum and minimum values of the total profit function to gain a sense of the salary ceilings that the business must adhere to avoid going bankrupt.

An engineer can utilize a function’s maximum and lowest values to identify the boundaries of the function in practical situations. If you can find a use for a train’s speed, for instance, knowing the train’s top speed can help you choose materials that will be durable enough to withstand the strain brought on by such high speeds and can be used to make brakes, rails, and other components that will allow the train to run smoothly.

A doctor can use the maximum and lowest values of the function defining the total bilirubin level in the bloodstream to estimate the dose that has to be given to various patients to return their bilirubin levels to normal. Hence, this can cure patients that face Jaundice disease early on and much more effectively. 

A power system engineer can use the maximum and minimum constraints of a generator and loads to determine the scheduling of different generators that will give the most optimum value of the cost of electricity generated to ensure the lowest possible cost of generation.

Thus, the maxima and minima play a large role in helping the world become much more efficient and progressive toward a more sustainable outcome. 

An Example Illustrating the Usage of Minimum in a Function

We are given a polynomial function written as below:

\[ f(x) = x^4-3x^3 + x^2 + x \]

Draw the above function on a graph and denote the Local and Global minima of the respective function.

Solution

As this is a polynomial of order four, it will have three extreme points. Now we have to identify, on the graph, the minimum points, and their values. Below is the figure that is plotted using GeoGebra for the given function:

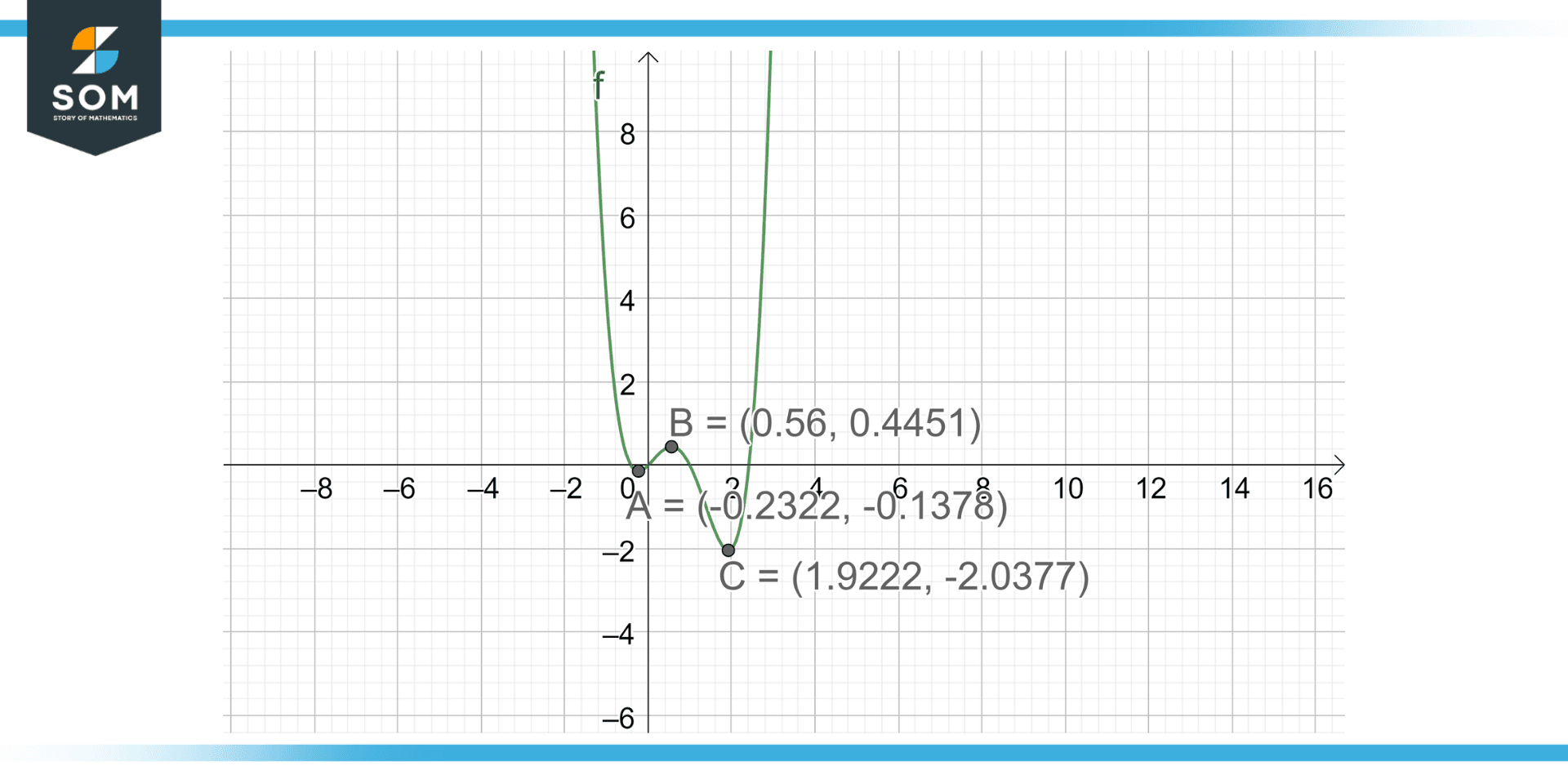
Figure 3: A curve showing Local and Global Minima for the function $ f(x) = x^4-3x^3 + x^2 + x $

Hence, according to the curve, we can see we have two minima,  occurring at A, x = -0.2322, and C, at x = 1.922. 

As the value at A, x= 1.922, is -2.0377 and at C, x = -0.2322, is -0.137, point C is the global minimum, whereas point A is the local minimum.

All the mathematical figures and graphs were created using GeoGebra.

Micro Definition < Glossary Index > Minuend Definition