JUMP TO TOPIC
Minuend|Definition & Meaning
Definition
The first operand in the operation of subtraction from which another operand called the subtrahend is subtracted is called the Minuend. For example, in the subtraction of 3 from 8 represented as 8 – 3, 8 is the minuend. Minuend must be greater than the subtrahend to produce a positive result.
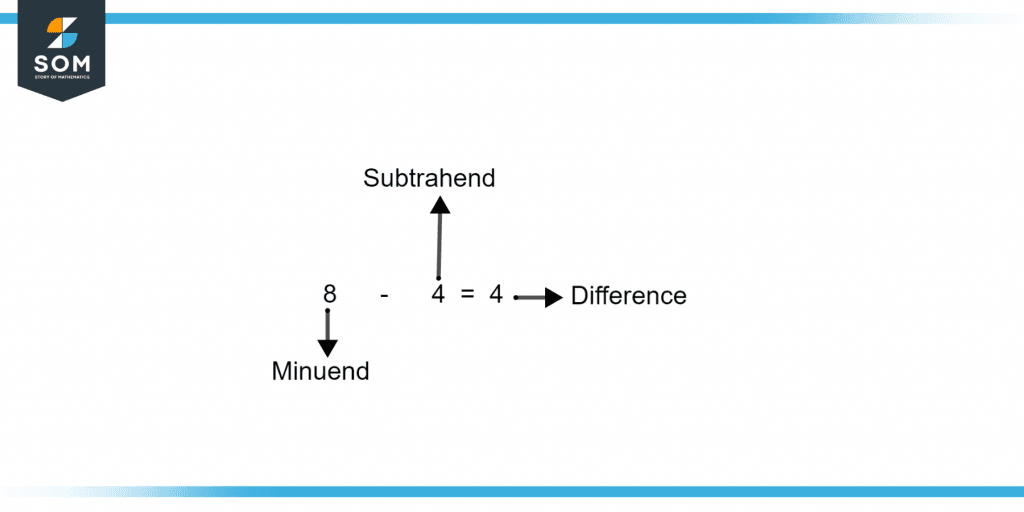
Figure 1 – Difference of two numbers
Figure 1 illustrates the difference between two numbers i.e., Minuend and Subtrahend.
Along with addition, multiplication, and division, subtraction is one of the four arithmetic operations and is denoted by the minus sign. Removal of items from a collection is represented by the operation of subtraction.
Subtraction can mean eliminating or lowering physical and abstract quantities utilizing a variety of things, such as negative integers, fractions, irrational numbers, vectors, decimals, functions, and matrices. However, it is typically linked with natural numbers in mathematics.
There are numerous significant patterns in subtraction. It is anticommutative, which means that altering the sequence alters the answer’s sign. Additionally, it is not associative, which means that when subtracting more than two integers, the method used matters. 0 is the additive identity, hence subtracting it has no effect on a number.
Subtraction adheres to a set of predictable rules, just like related operations like sum and multiplication. It is feasible to show each of these rules, beginning with the subtraction of integers and extending to real numbers and beyond. In general binary operations, abstract algebra looks at these patterns.
The three components of a subtraction problem are the minuend, subtrahend, and difference. The difference is the outcome after subtracting from the minuend, the subtrahend, and the beginning point, respectively.
If you are aware of two of the three parts, you may locate the missing one. Here are three different calculators we created. The first calculation computes the difference, the second computes the minuend, and the third computes the subtrahend.
The Latin term “minuend,” from which the English word “minuend” is derived, implies “to decline or lessen in value.” The quantity from which another quantity is to be reduced is known as the base quantity. In equation a – b = c, an is the minuend.
In subtraction, the starting integer from which a number is subtracted or lowered is referred to as the minuend. a subtraction equation’s initial digit. The quantity that will be subtracted from another quantity (the Subtrahend).
Three Sections of Subtraction
A subtraction equation is divided into three parts: the minuend, the subtrahend, and the difference.
The minuend is defined as the maximum number or total from which a component would be subtracted or subtracted. The part of the minuend that is omitted is referred to as the subtrahend. the sum you wish to remove.
The second word in a subtraction sentence is called a subtrahend. To get the outcome, the difference is subtracted from the minute. The amount over the gap is subtracted vertically or in columns. The subtrahend is often smaller than the minuend in a column subtraction operation.
After subtraction, this part is what remains. The difference is calculated by taking two integers apart. Despite the fact that we frequently discuss variances in how things seem, sound, and even taste, arithmetic shows how much two numbers may differ in amount.
Subtraction Of Integers
On the real line shown in figure 2, integer subtraction may be done.
Figure 2 – Subtraction of integers on Real Line
Figure 3 shows that if we have to remove 3 from 4 and then move 4 spaces to the left, the result is -1.
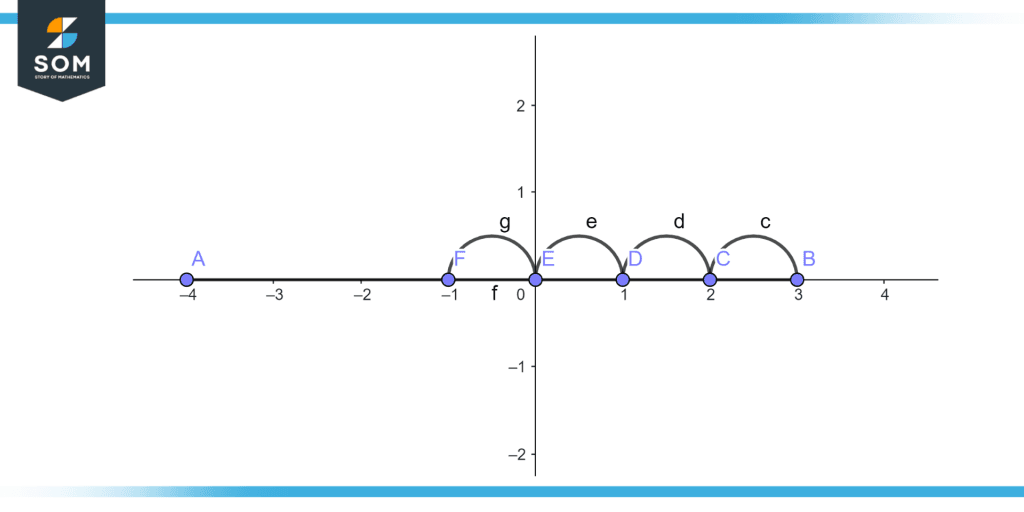
Figure 3 – Subtraction Of Integers
Subtraction of Natural Numbers
Natural numbers cannot be subtracted in a closed manner because the difference cannot be a natural number unless the minuend is larger than or equal to the subtrahend. One cannot, for instance, subtract 26 from 11 and get a natural number. One of two methods is used in such a case:
A partial function of subtraction results when 26 is attempted to be subtracted from 11. The outcome of subtracting 26 from 11 is 15, thus providing the answer as an integer that represents a negative number.
Subtraction of Real Numbers
Only the operations addition and multiplication, as well as the unary operations that result in the additive and multiplicative inverses, may be used to describe the field of real numbers. It is thus possible to describe the subtraction of one real number (the subtrahend) from another using the addition of the minuend and the additive inverse of the subtrahend (the minuend).
For instance, 3 + (-$\pi$) Equals 3 – $\pi$. Alternately, subtraction and division are binary operations that might be considered fundamental in place of these unary operations.
Application of Minuend in Real Life
You can do subtraction operations fast and simply if you have a good understanding of the idea of the minuend. For instance, being familiar with this idea will make it simple for you to determine how much money you have left after making a purchase at a store.
Some Examples of Minuend
Example 1
a) Find the Minuend if the difference is equal to 32 and the subtrahend is equal to 20.
b) Find the Minuend if the difference is equal to 25 and the subtrahend is equal to 2.
c) Find the difference if the minuend is equal to 20 and the subtrahend is equal to 10.
Solution
a) As the formula to calculate the difference is given as:
Minuend – Subtrahend = Difference
As given, the difference is equal to 32, and the subtrahend is equal to 20. By the formula, we have:
Minuend – 20 = 32
Minuend = 32 + 20
Minuend = 52
The minuend is equal to 52.
b) As the formula to calculate the difference is given as
Minuend – Subtrahend = Difference
As given, the difference is equal to 25, and the subtrahend is equal to 20. By the formula, we have:
Minuend – 20 = 25
Minuend = 25 + 20
Minuend = 45
The minuend is equal to 45.
c) As the formula to calculate the difference is given as:
Minuend – Subtrahend = Difference
As given, the minuend is equal to 20, and the subtrahend is equal to 10. By the formula, we have:
20 – 10 = 10
The difference is equal to 10.
Example 2
Ali had \$48 in her bank account. She withdrew \$39. How much money is in her bank account?
Solution
To evaluate the difference, we have the formula:
Minuend – Subtrahend = Difference
The total amount in the bank, which is \$48, is the minuend, and the subtrahend is equal to \$39, so to evaluate the difference, we can put the values:
Difference = \$48 – \$39
Difference = \$48 – \$39
Difference = \$9
All images were created using GeoGebra.
