Minus|Definition & Meaning

Pictorial Intuition 

The following figures and explanations describe the intuitive reasoning behind the minus or subtraction operator:

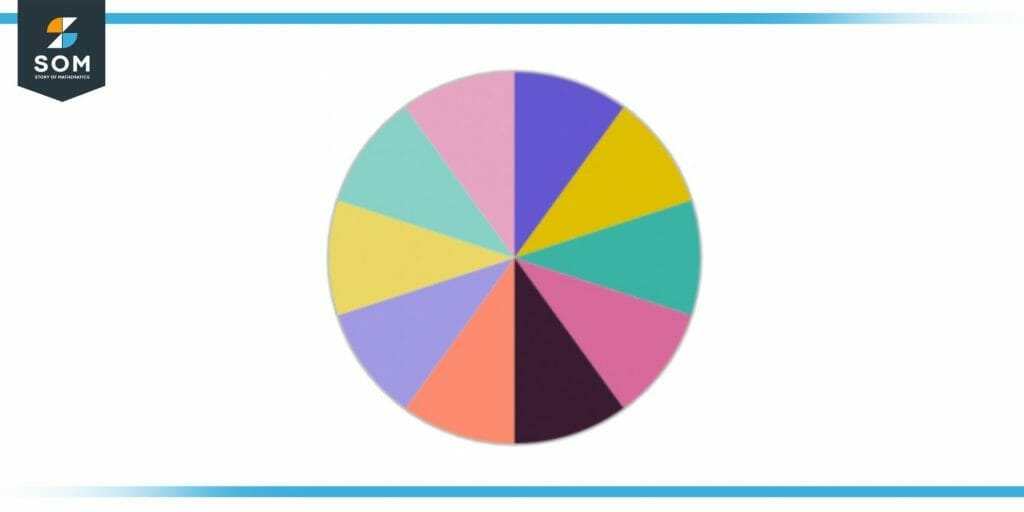
Figure 1: Ten Equal Parts of a Pie

Figure 1 shows a pie chart that has been divided into 10 equal sectors. The total area of the pie represents the number 10. Now suppose that we wanted to perform the operation ten minus three. This mathematical operation is equivalent to removing three parts out of the total ten parts of the pie, as illustrated in the figure below:

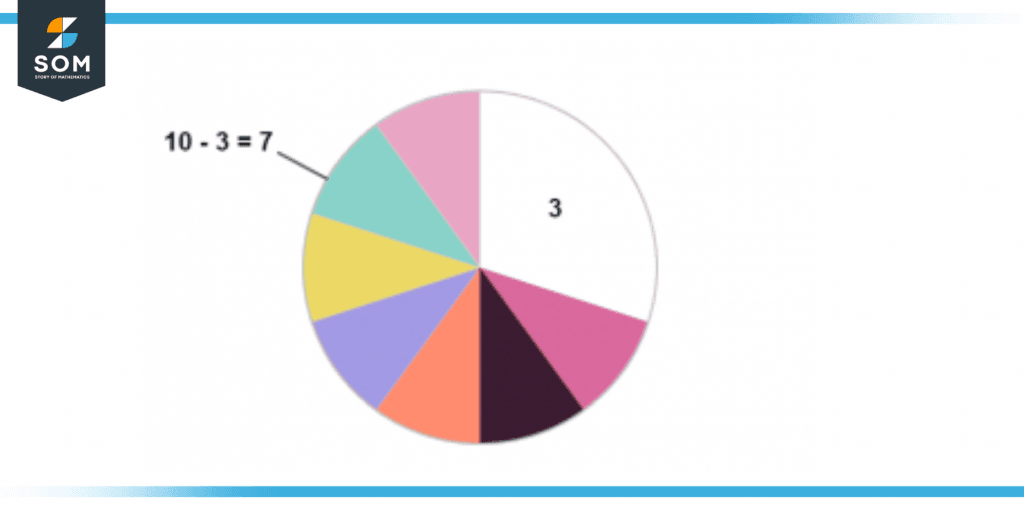
Figure 2: Ten Minus Three Operation

The above figure shows that if we remove three parts, we are left with seven parts which is the result of the operation ten minus three. This proves graphically that 10 – 3 = 7. Consider another case where we wanted to perform the operation ten minus five. This mathematical operation is equivalent to removing five parts out of the total ten parts of the pie, as illustrated in the figure below:

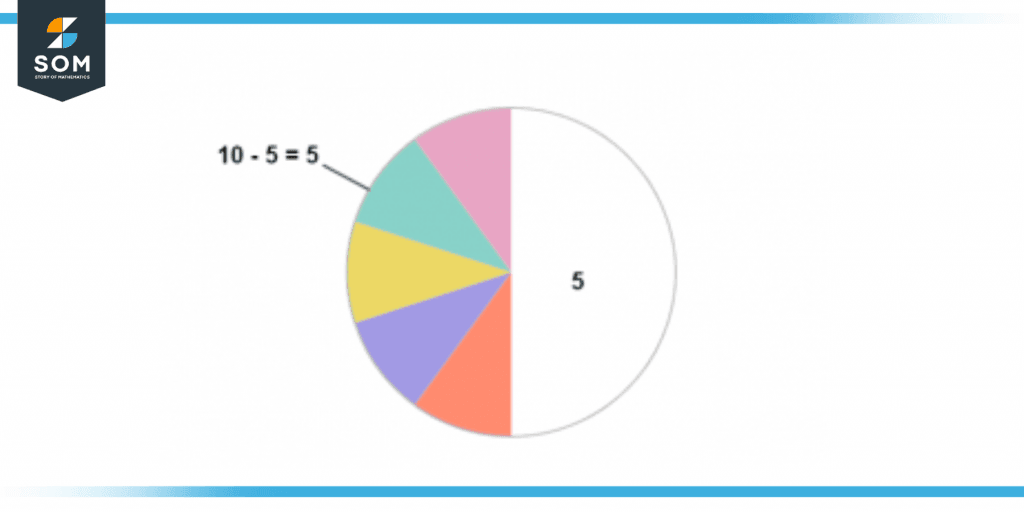
Figure 3: Ten Minus Five Operation

The above figure shows that if we remove five parts, we are left with five parts which is the result of the operation ten minus five. This proves graphically that 10 – 5 = 5. We can understand the operation 10 – 7 = 3 in a similar manner utilizing figure 4 given below:

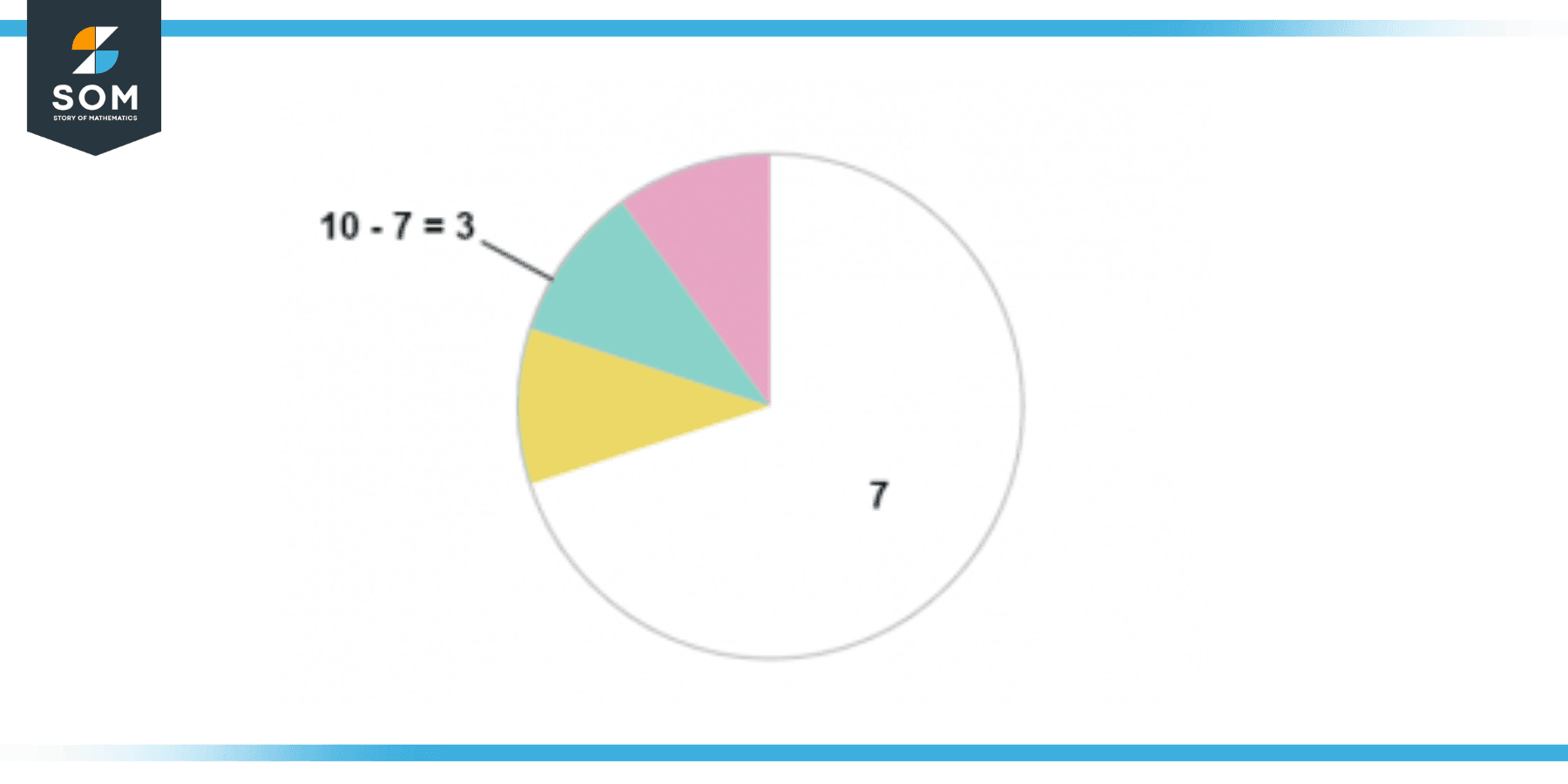
Figure 4: Ten Minus Seven Operation

Explanation of Minus Operation

A minus sign also refers to the subtraction of a part of a given value from itself. It is such a mathematical process where the subtraction method involves pruning or cutting out a portion of the given numerical value and subtracting it from itself. This process and the background concepts are further explained in detail in the following sections with the help of very easy-to-relate numerical and practical examples.

Subtraction is a very fundamental concept taught in elementary schools as a basis for the whole mathematics along with the other basic operations of addition, multiplication, and division. The key idea behind the subtraction process is very easy to learn.

Let us consider an example to understand its concept. Suppose you went out and bought twelve apples and must share two apples with your sibling. Now you intuitively know that if you give two apples to your sibling, you will only be left with ten apples. The operation that you performed in drawing this result is called minus or subtraction.

Carrying forward the above example, one can say that you performed the mathematical operation: twelve minus two equals ten. In symbolic terms, we would write this operation as 12 – 2 = 10.

Negative or additive inverse is a very common sighting in almost all kinds of numerical problems. It is used to cancel out the effects of some physical quantity when we talk about the physical sense of things. This very same operation is used to represent the negative integers.

Guidelines for Solving Minus Numerical Problems

Although the above figures perfectly develop the graphical or intuitive understanding of the subject, evaluating the minus operator in numerical problems is a different subject. Now we have to perform certain numerical procedures to calculate the final answer. The mathematical procedure for evaluating a subtraction can be reduced to a simpler addition problem by using the following step-by-step method:

Step 1: Write the problem in mathematical form. For example, 10 – 6.

Step 2: Decompose the first operand into parts such that one of them is the additive inverse of the second operand. For example, 10 can be divided into two parts, +4 and +6. Here +6 is the additive inverse of -6, which is the second operator. The expression reduces to 4 + 6 – 6.

Step 3: Now that we have a number and its additive inverse added together, we can use the additive inverse property and sum both of these equal to zero. In above example, + 6 – 6 = 0.

Step 4: Substituting the above solution results in the final answer. In above example, 4 + 6 – 6 = 4 + 0 = 4.

Example Numerical Problems

The mathematical process of evaluating minus or subtraction problems is explained with the help of numerical examples in this section. Here we suppose that we wanted to calculate the results of the following minus operations:

(a) 55 minus 38

(b) 100 minus 10

(c) 4 minus 5

(d) 1.55 – 0.55

Solutions

(a) 55 minus 38

Here 55 can be decomposed into two parts, 17 and 38, such that 17 plus 38 equals 55:

55 – 38 = ( 17 + 38 ) – 38 = 17 + 38 – 38

Here + 38 and – 38 are the additive inverse or negative of one another, so their sum is equal to zero:

55 – 38 = 17 + 0 = 17

(b) 100 minus 10

Here 100 can be decomposed into two parts, 90 and 10, such that 90 plus 10 equals 100:

100 – 10 = ( 90 + 10 ) – 10 = 90 + 10 – 10

Here + 10 and – 10 are the additive inverse or negative of one another, so their sum is equal to zero:

100 – 10 = 90 + 0 = 90

(c) 4 minus 5

Here 4 can be decomposed into two parts, -1 and +5, such that -1 plus 5 equals 4:

4 – 5 = ( -1 + 5 ) – 5 = – 1 + 5 – 5 = – 1 + 0 = – 1

Here +5  and -5 are the additive inverse or negative of one another, so their sum is equal to zero:

4 – 5 = – 1 + 0 = – 1

(d) 1.55 minus 0.55

Here 1.55 can be decomposed into two parts, 1 and 0.55, such that 1 plus 0.55 equals 1.55:

1.55 – 0.55 = ( 1 + 0.55 ) – 0.55 = 1 + 0.55 – 0.55

Here + 0.55 and – 0.55 are the additive inverse or negative of one another, so their sum is equal to zero:

1.55 – 0.55 = 1 + 0 = 1

All mathematical drawings and images were created with GeoGebra.

Minuend Definition < Glossary Index > Minute Angles Definition