JUMP TO TOPIC
Minute Angle|Definition & Meaning
Definition
A second is 1/3600 of a degree. Three hundred and sixty degrees make a whole circle. Each of the sixty sections that make up each degree is 1/60th of a degree. These sections are known as minutes. A minute is divided into 60 equal sections, each of which is 1/60th of a minute. These sections are termed seconds.
Three hundred and sixty degrees are contained in a whole circle. Each of the sixty sections that make up each degree is 1/60th of a degree. These sections are known as minutes.
A minute is divided into 60 equal sections, each of which is 1/60th of a minute. These sections are termed seconds.
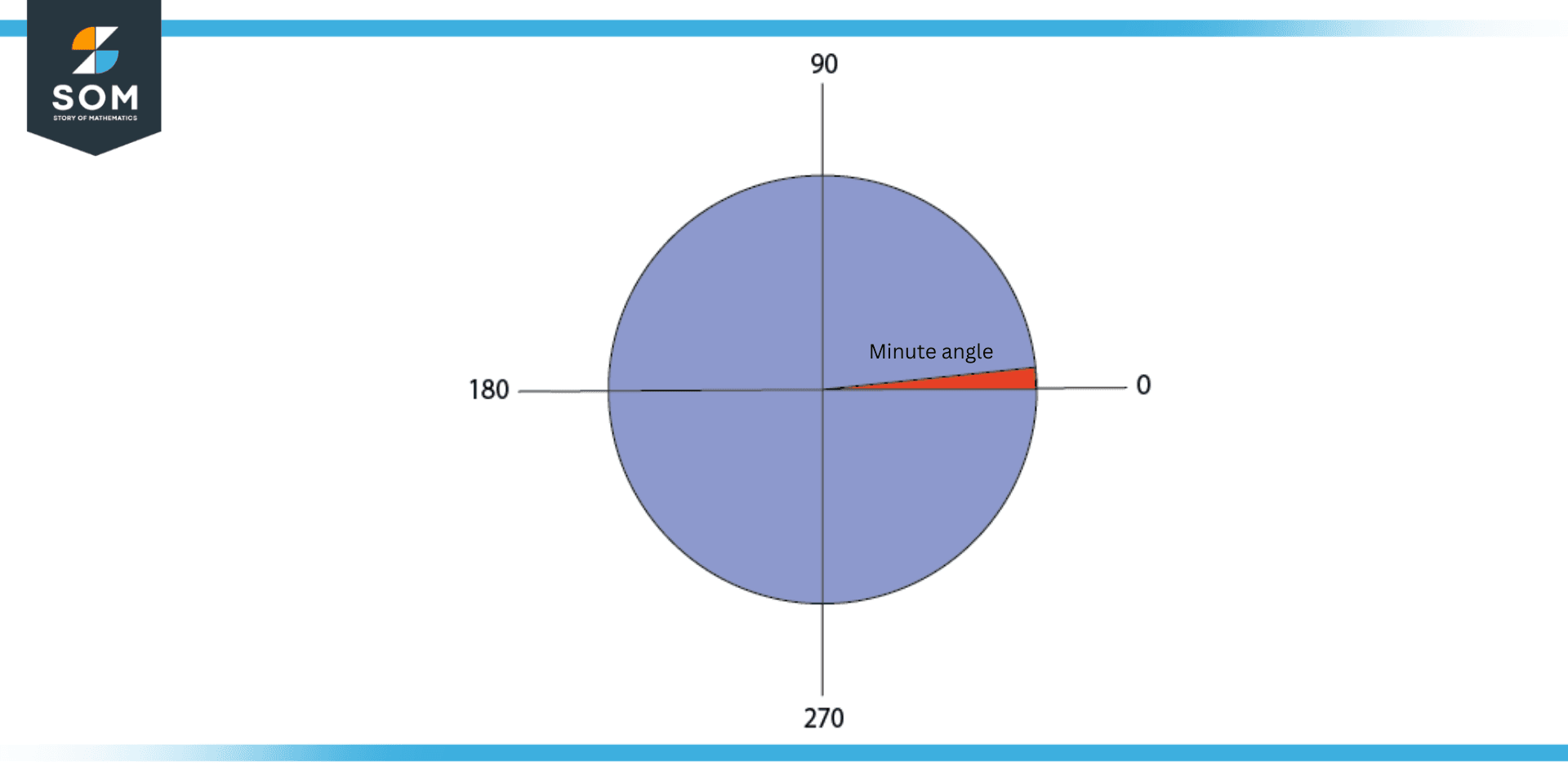
Figure 1: A minute angle is extremely small. This is a zoomed-in version of the minute angle expressed on a circle.
The use of the terms minute and second here has nothing to do with how those terms are typically used to refer to time periods.
1 degree = 60’
1 minute = 60’’
1 degree = 3600’’
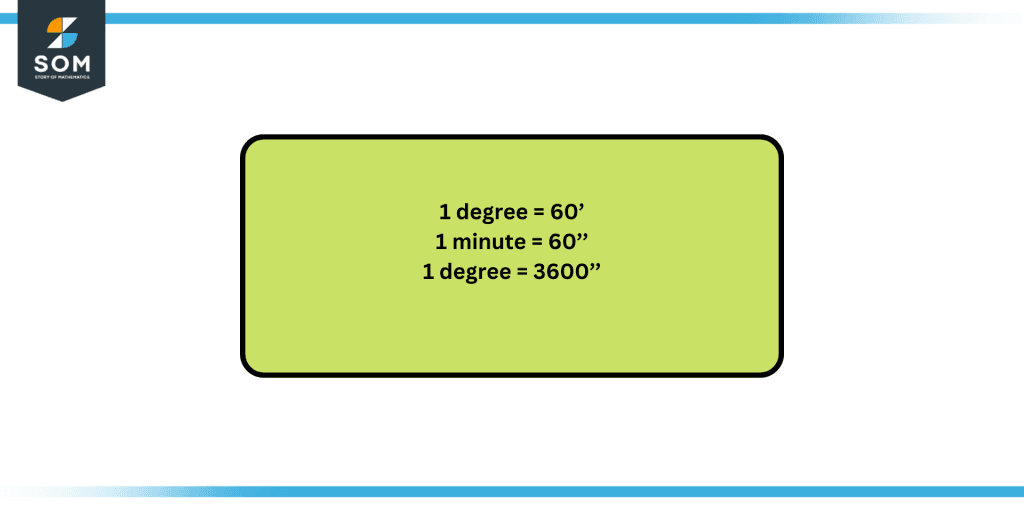
Figure 2: Degree, minutes and seconds expressed as equivalent terms.
Reason for Converting Degrees Into Minutes
Because hours are split into minutes and minutes are further divided into seconds, how will you claim that it is neither five o’clock nor six o’clock? Simply mention it, for instance, 20 past five.
Similar to how minutes and seconds are used to divide angles, minutes and seconds are used to assist you to explain that an angle may not be 100 degrees or 105 degrees but anything in between them, for instance, 100 degrees 45 minutes is equivalent to 100.75 degrees.
Using D°M’S’’ Locating Coordinates on the Globe
Using latitude and longitude, we can locate any place on the planet for positioning. These coordinates are measured in decimal degrees or D°M’S’’. Longitude coordinates can be divided between -180 and +180 degrees, whereas latitude lines span between -90 and +90 degrees.
Any point on Earth can be identified by its longitude and latitude using a geographic coordinate system (GCS). We utilize angles expressed in degrees or more precisely, D°M’S’’ from the earth’s center to any point on its surface since a GCS employs a sphere to describe locations on the planet.
The intersection of the equator and Prime Meridian is at the coordinates (0°0’0’’N, 0°0’0’’E) which is amusingly just all ocean.
Positions are generally expressed in degrees, minutes, and seconds of angles for two measurements: latitude, which is the angle north or south of the equator, and longitude, which refers to the angle east or west of the Prime Meridian.
Using degrees-minutes-seconds (D°M’S’) is one technique to represent spherical coordinates (latitudes and longitudes). The span of minutes and seconds is 0 to 60. For instance, the geographic coordinates of Paris are as follows when stated in degrees-minutes-seconds:
Latitude: 48 degrees, 51 minutes, 52.97 seconds N
Longitude: 2 degrees, 20 minutes, 52.97 seconds E
However, decimal degrees can also be used to indicate geographic coordinates. It’s just another format in which one can portray the same location. Here is the city of Paris, for instance, expressed in decimal degrees:
Latitude: 48.864716 N
Longitude: 2.349014 E
Importance and Relation With Time
The year was thought to be roughly 360 days long in the early days of human history. They lacked accurate measuring equipment, but it was simple enough just to add a month every six years or so until they became aware of the accumulating change.
We owe the concept of 360 degrees in a circle to the Babylonians since it was a discernible cycle that led to the idea that a circle should have that many segments. It was easy to divide 360 into many different numbers, making it a useful number.
They divided each degree into 60-minute increments in order to achieve more accuracy. They quickly needed even greater accuracy, so they separated every minute into a second, the second order minute. Babylonian trigonometry is still in use today.
As transportable and precise clocks proliferated, it was clear that the position of the sun varied around the globe. By comparing the position of the sun or stars to a reference time, we were able to determine our location.
However, a degree is a rather significant distance. A degree of arc at the equator is 1/360 of a circumference of around 25000 miles (actually 24901). As a result, 69.17 miles are equal to one degree of arc. That equates to around 365,215 feet.
The result of dividing that by 60 is approximately 6087 feet. One degree of arc is equivalent to one sea mile since it is about 15% longer than a standard mile (5280 feet).
Examples Explaining the Concept of Degrees, Minutes, and Seconds
Example 1
Convert 125.45° degrees into D°M’S” form.
Solution
As we are aware that 1 degree is equal to 60’ and 1 minute is equal to 60’’, so let us use this to calculate the required result.
First, we have to split the whole number and the decimal parts:
125.45° = 125° + 0.45°
= (125°) + (45/100°)
= (125°) + (9/20°)
Multiplying 9/20 by 1°:
= (125°) + (9/20 .1°)
As 1° = 60’:
= (125°) + (9/20 .60’)
= (125°) + (9×3’)
Or:
= 125° + 27’
Now adding the seconds part:
= 125° + 27’ + 0’’
The conversion results in:
= 125° 27’ 0’’
Hence, the decimal has been converted into D°M’S” form.

Figure 3: Decimal notation converted into D°M’S’’ notation.
Example 2
Convert 30°15’10’’ into decimal notation.
Solution
In the first step, let us split the D°M’S’’ notation into parts:
= 30° + 15’ + 10’’
We can write the above expression as:
= 30° + 15. 1’ + 10.1’’
Now, as 1’ = 1/60° and 1’’ = 1/3600°, let us plug in their values in the above expression:
= 30° + 15. 1/60° + 10.1/3600°
= 30° + 0.25° + 0.0027°
= 30.2527°
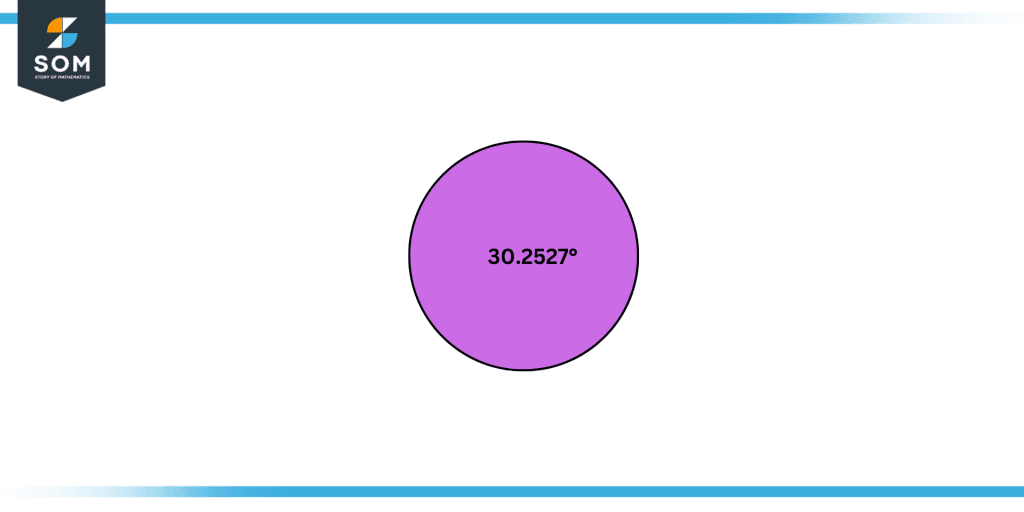
Figure 4: D°M’S’’ notation converted into decimal notation.
Example 3
Convert 45°30’20’’ into radians.
Solution
We will have to convert the above expression into degree notation first. We will follow the same pattern s we did previously.
Let us split the D°M’S’’ notation into parts:
= 45° + 30’ + 20’’
We can write the above expression as:
= 45° + 30. 1’ + 20.1’’
Now, as 1’ = 1/60° and 1’’ = 1/3600°, let us plug in their values in the above expression:
= 45° + 30. 1/60° + 20.1/3600°
= 45° + 0.5° + 0.0055°
= 45.5055°
Now that we have converted our D°M’S’’ notation into decimal notation, let us convert it into radians now:
= 45.5055°. (π/180)
= 0.2528π
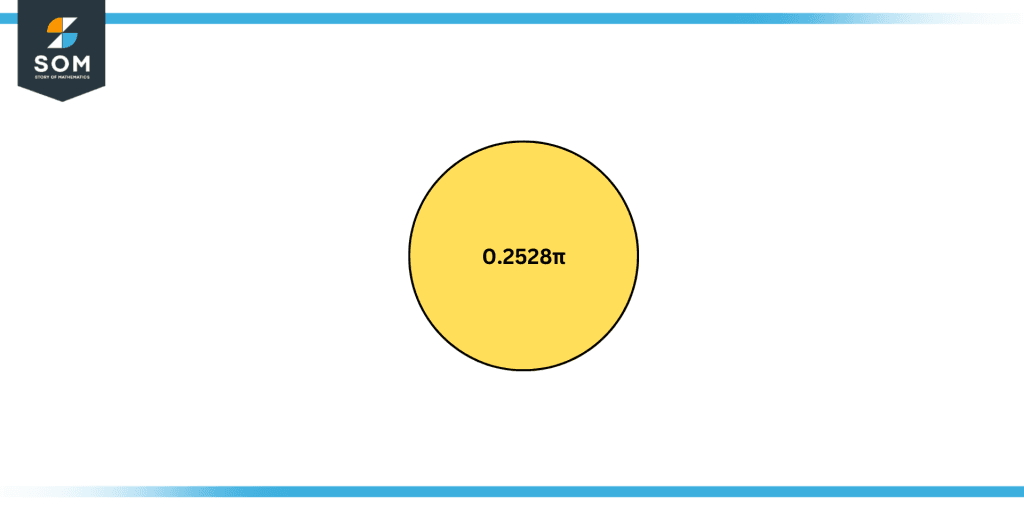
Figure 5: D°M’S’’ notation converted into radians.
Therefore, we have converted our D°M’S’’ notation into radians.
All images/mathematical drawings were created with GeoGebra.
