JUMP TO TOPIC
Multiple|Definition & Meaning
Definition
Multiple is the result of multiplying a number with another number. In other words, a larger number is a multiple of a smaller number if dividing the larger number by the smaller one produces a zero remainder. Therefore, 6 is a multiple of 2 and 3 because 2 x 3 = 6.
In mathematics, the term “multiple of the numbers” refers to the result of multiplying two whole numbers together. For example, 5 multiplied by 6 equals 30, therefore, 30 is now a multiple of both 5 and 6. In accordance with this, a multiple would be a number that, when divided by the provided number, results in no remainder at the end of the division. This is the definition of a multiple for any given number.
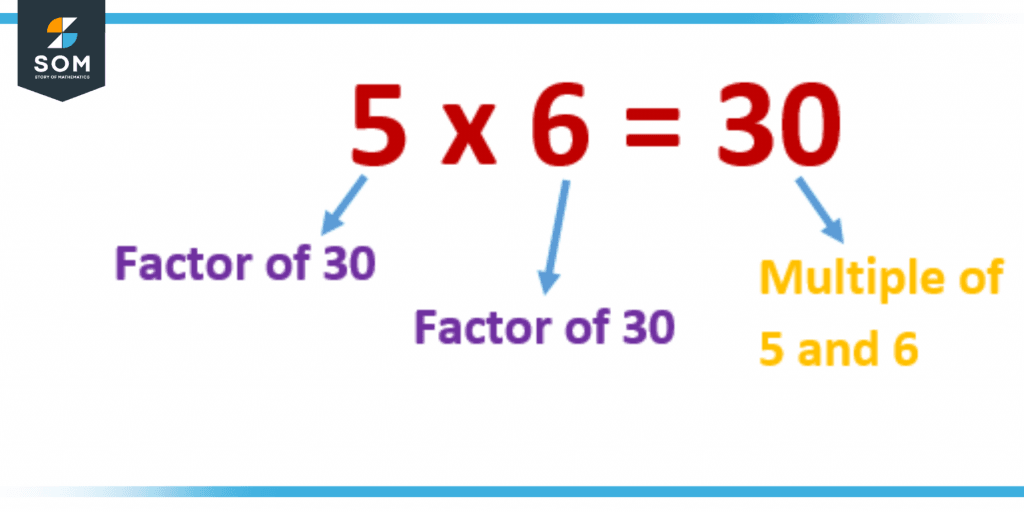
Figure 1 – Multiple of 5 and 6
The figure above shows the multiple of 5 and 6, which is 30. These both factors are different, but when the number is multiplied by 1, the multiple will be the number itself.
Illustration of Multiples
Mathematics is the study of numbers, their classifications, and the ideas that are associated with them. It is a numerical game. The area of mathematics known as arithmetic focuses on the qualities and operations that can be performed on numerical values.
In the primary mathematics grades, the concepts of multiples and factors are studied hand in hand as two essential building blocks. A number is considered to be a factor if, after being used to divide another number, it does not produce a remainder.
A multiple, on the other hand, is a number that is arrived at by the multiplication of a given number by another. While a number’s factors can be counted, a number’s multiples can never be exhausted. Every single number is really a multiple of both 0 and the number itself.
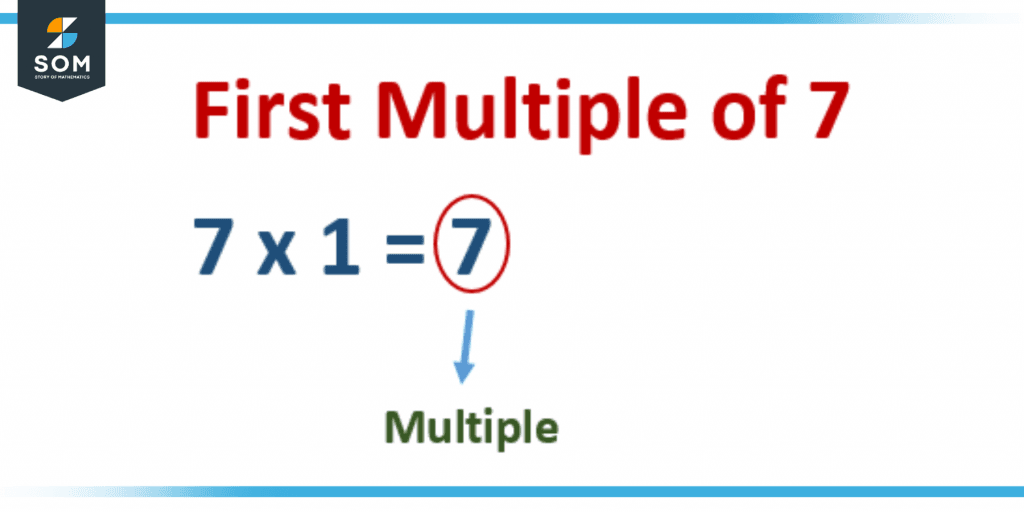
Figure 2 – First Multiple is the number itself
The first multiple of the number 7 is 7 itself because when it is multiplied with any other factor that is 1, it results in the same number.
A Deeper Dive Into Finding Multiples
The two terms, factors and multiples, may, at first glance, appear to be interchangeable; however, there are a number of key distinctions between the two that have been outlined in this article.
You can take any number with a single digit that is not zero, such as the number 2, and add it to itself whatever amount of times you wish. Let’s move on and perform the addition of the number 2 five times. This can be written down as two plus two plus two plus two plus two (2 + 2 + 2 + 2 + 2), and the result of the issue would be ten.
This new number will be referred to as the result of 2 times 5 from now on. Similarly, if we were to take the number 5 and add it twice, we would arrive at the number 10. The number 10 is the result of multiplying 5 by 2.

Figure 3 – Multiple of 10 by Multiplication and Addition Method
The 10 is therefore the multiple of 5 and a multiple of 2, as 2 multiplied by 5 yields 10, while it is also a multiple of 2 as 5 multiplied by 2 yields 10.
If you have been following along thus far, then understanding multiples and all of the concepts associated with them, which are covered in this article, will be quite simple for you to do. You will have plenty of opportunities to practice along with the examples and questions provided, as was previously said.
At the conclusion of the article, you will find the answers to each of the practice questions.
Methods To Find Multiples
There are different ways to find multiples of different numbers. Different methods to find multiples are listed below:
- Least Common Multiple
- Grid Multiplication Method
Least Common Multiple
Discovering the number that is the LCM of two and more than numbers is not only a fascinating approach to solving problems, but it is also occasionally important. Finding the least common multiples of two or more numbers can be done through a few different methods.
The following are the most typical approaches: Listing Method, Ladder Method, and Lcm of Mixed Numbers LCM, etc.

Figure 4 – LCM of 12 and 18
The above figure shows the least common multiple of 12 and 18.
Grid Multiplication Method
This grid method which is also termed both the box method and also the grammar school approach or is an effective place to begin learning multiples as well as the calculations with higher numbers that are greater than 10. Using this approach, the process of manually multiplying numbers is broken down into three distinct parts.
The first thing to do is to construct a grid or table, with the numbers you need to multiply appearing in the first row and the first column, respectively. The first box won’t have anything put in it. The second stage in this process involves multiplying all of the integers that are located in the columns and the rows together. A comprehension of addition is required for the third level.
Utilizing this approach makes it effortless to dissect and reduce the complexity of the components that contribute to that number.
Example Problems of Multiples
Example 1
Write the first 8 multiples of 11 by multiplication and addition method?
Solution
By Multiplication Method:
11 x 1 = 11
11 x 2 = 22
11 x 3 = 33
11 x 4 = 44
11 x 5 = 55
11 x 6 = 66
11 x 7 = 77
11 x 8 =88
By Addition Method:
11
11 + 11 = 22
11 + 11 + 11 = 33
11 + 11 + 11 + 11 = 44
11 + 11 + 11 + 11 + 11= 55
11 + 11 + 11 + 11 + 11 + 11= 66
11 + 11 + 11 + 11 + 11 + 11 + 11= 77
11 + 11 + 11 + 11 + 11 + 11 + 11 + 11= 88
So here, 11, 22, 33, 44, 55, 66, 77, and 88 are the multiples of 11.
Example 2
Write some common multiples of 5 and 10.
Solution
Multiple of 5:
5, 10, 15, 20, 25, 30, 35, 40, 45, 50
Multiples of 10:
10, 20, 30, 40, 50
So the common multiples of 5 and 10 are 10, 20, 30, 40, and 50.
All the figures above are created on GeoGebra.
